中考数学二轮复习考点提分特训专题07 五大最值问题模型（2份打包，原卷版+解析版）

这是一份中考数学二轮复习考点提分特训专题07 五大最值问题模型（2份打包，原卷版+解析版），文件包含中考数学二轮复习考点提分特训专题07五大最值问题模型原卷版doc、中考数学二轮复习考点提分特训专题07五大最值问题模型解析版doc等2份试卷配套教学资源，其中试卷共106页， 欢迎下载使用。
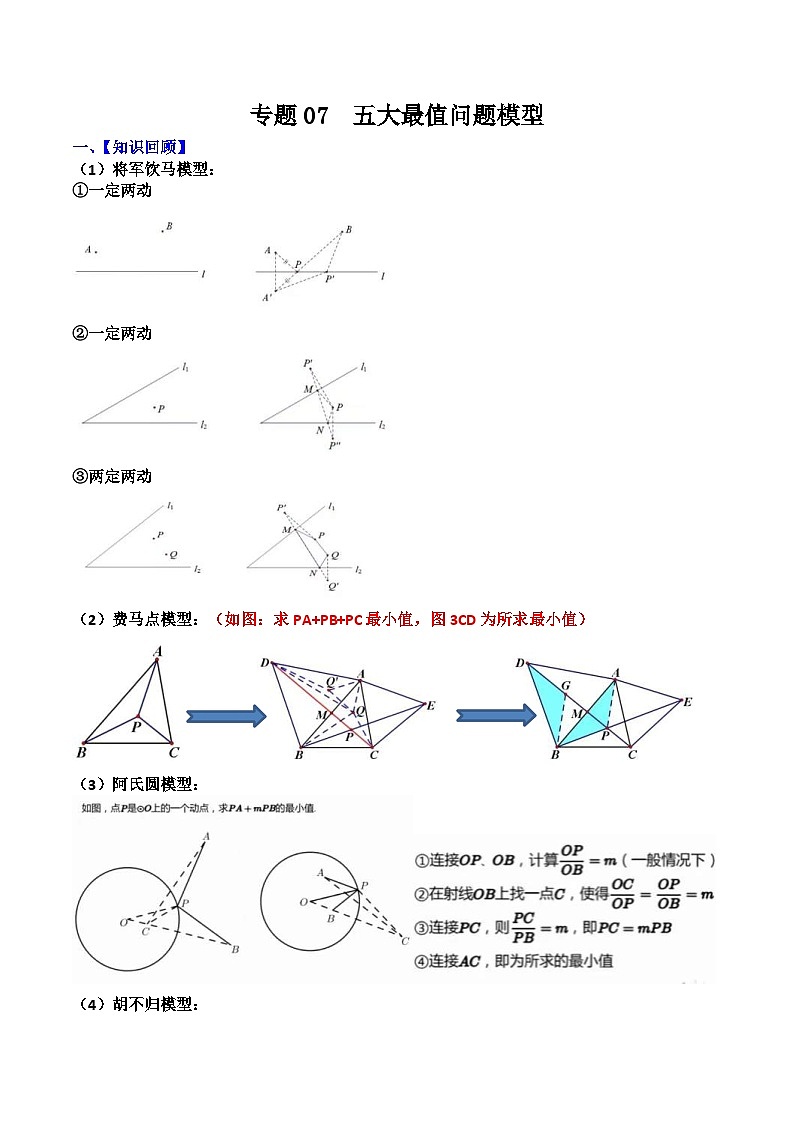
（1）将军饮马模型：
①一定两动
②一定两动
③两定两动
（2）费马点模型：（如图：求PA+PB+PC最小值，图3CD为所求最小值）

（3）阿氏圆模型：
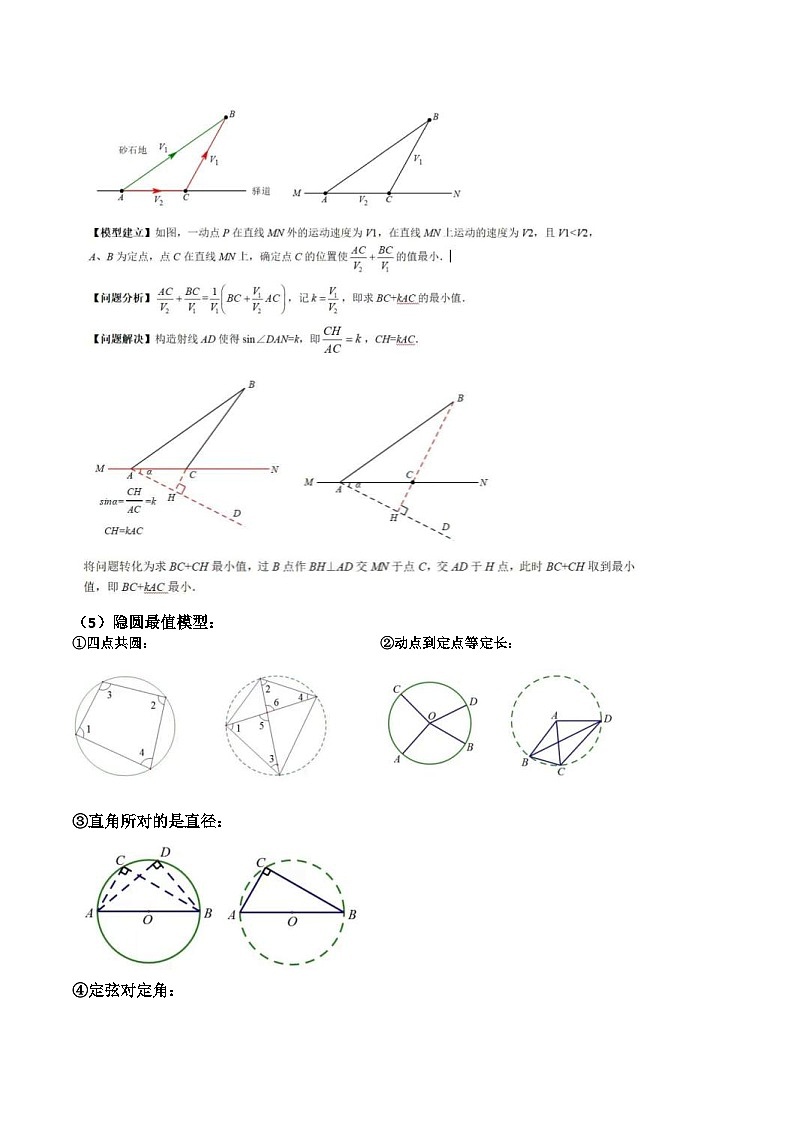
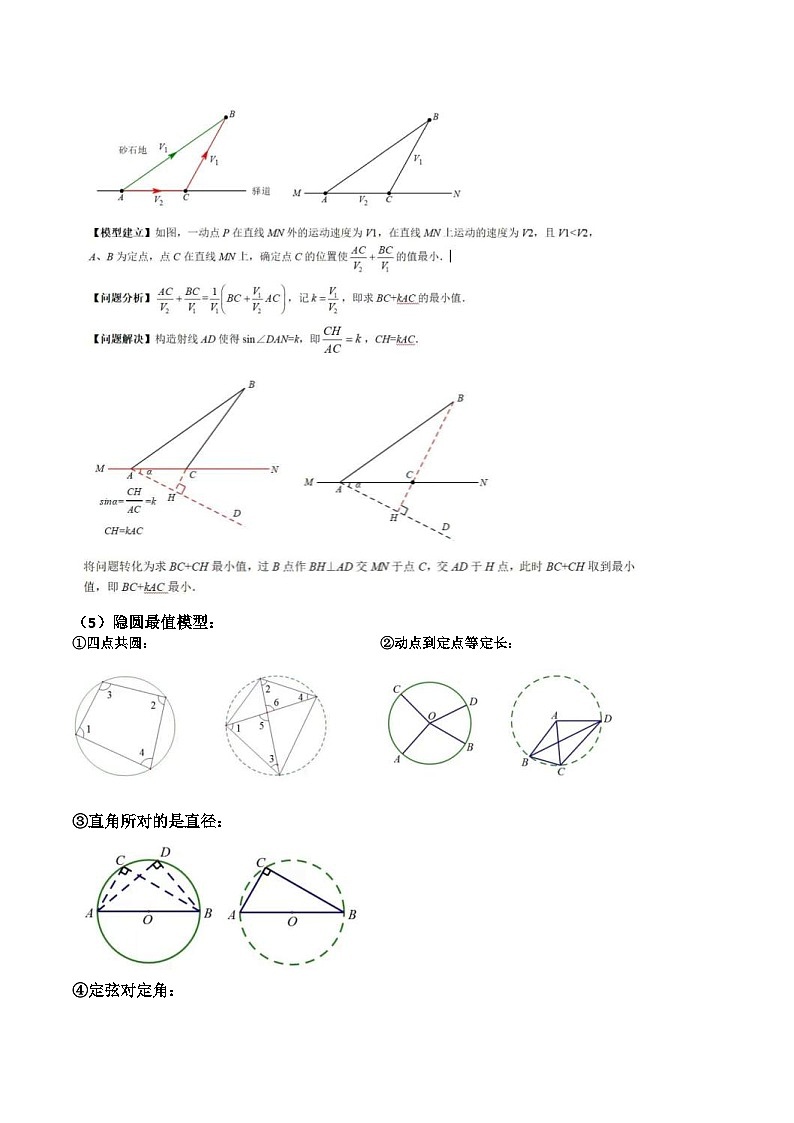
（4）胡不归模型：
（5）隐圆最值模型：
①四点共圆： ②动点到定点等定长：

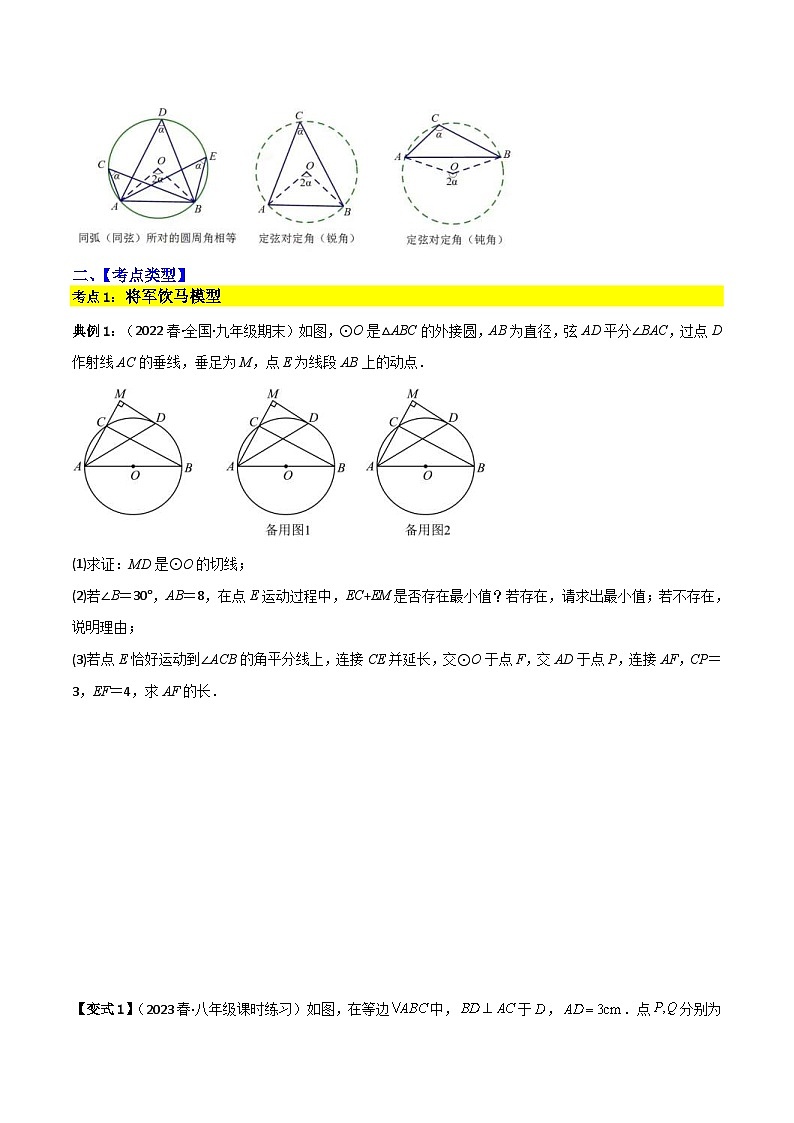
③直角所对的是直径：
④定弦对定角：
二、【考点类型】
考点1：将军饮马模型
典例1：（2022春·全国·九年级期末）如图，⊙O是△ABC的外接圆，AB为直径，弦AD平分∠BAC，过点D作射线AC的垂线，垂足为M，点E为线段AB上的动点．
(1)求证：MD是⊙O的切线；
(2)若∠B＝30°，AB＝8，在点E运动过程中，EC+EM是否存在最小值？若存在，请求出最小值；若不存在，说明理由；
(3)若点E恰好运动到∠ACB的角平分线上，连接CE并延长，交⊙O于点F，交AD于点P，连接AF，CP＝3，EF＝4，求AF的长．
【变式1】（2023春·八年级课时练习）如图，在等边 SKIPIF 1 < 0 中， SKIPIF 1 < 0 于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．点 SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 上的两个定点且 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 上一动点，连接 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为______ SKIPIF 1 < 0 ．
【变式2】（2023春·山东青岛·九年级专题练习）如图，点P是 SKIPIF 1 < 0 内任意一点， SKIPIF 1 < 0 ，点M和点N分别是射线 SKIPIF 1 < 0 和射线 SKIPIF 1 < 0 上的动点， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 周长的最小值是______．
【变式3】（2022春·贵州铜仁·八年级统考期末）如图，已知一次函数y＝kx＋b的图像经过A（1，4），B（4，1）两点，并且交x轴于点C，交y轴于点D．
(1)求该一次函数的表达式；
(2)若y轴存在一点P使PA＋PB的值最小，求此时点P的坐标及PA＋PB的最小值；
(3)在x轴上是否存在一点M，使△MOA的面积等于△AOB的面积；若存在请直接写出点M的坐标，若不存在请说明理由．
考点2：费马点模型
典例2：（2021秋·四川成都·九年级成都实外校考阶段练习）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，P是 SKIPIF 1 < 0 内一点，求 SKIPIF 1 < 0 的最小值为______．
【变式1】（2022秋·全国·九年级专题练习）在正方形ABCD中，点E为对角线AC（不含点A）上任意一点，AB= SKIPIF 1 < 0 ；
（1）如图1，将△ADE绕点D逆时针旋转90°得到△DCF，连接EF；
①把图形补充完整（无需写画法）； ②求 SKIPIF 1 < 0 的取值范围；
(2)如图2，求BE+AE+DE的最小值．
【变式2】（2022春·全国·九年级专题练习）如图，正方形 SKIPIF 1 < 0 的边长为4，点 SKIPIF 1 < 0 是正方形内部一点，求 SKIPIF 1 < 0 的最小值．
【变式3】（2022春·江苏·九年级期末）如图，在平面直角坐标系xy中，点B的坐标为(0，2)，点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 轴的正半轴上， SKIPIF 1 < 0 ，OE为△BOD的中线，过B、 SKIPIF 1 < 0 两点的抛物线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴相交于 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两点（ SKIPIF 1 < 0 在 SKIPIF 1 < 0 的左侧）.
（1）求抛物线的解析式；
（2）等边△ SKIPIF 1 < 0 的顶点M、N在线段AE上，求AE及 SKIPIF 1 < 0 的长；
（3）点 SKIPIF 1 < 0 为△ SKIPIF 1 < 0 内的一个动点，设 SKIPIF 1 < 0 ，请直接写出 SKIPIF 1 < 0 的最小值,以及 SKIPIF 1 < 0 取得最小值时，线段 SKIPIF 1 < 0 的长.
考点3：阿氏圆模型
典例3：（2023春·江苏·九年级校考阶段练习）如图，正方形 SKIPIF 1 < 0 的边长为4， SKIPIF 1 < 0 的半径为2， SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的动点，则 SKIPIF 1 < 0 的最大值是______．
【变式1】（2022春·江苏·九年级专题练习）如图，边长为4的正方形，内切圆记为⊙O，P是⊙O上一动点，则 SKIPIF 1 < 0 PA＋PB的最小值为________．
【变式2】（2023秋·重庆九龙坡·九年级重庆市育才中学校考期末）已知 SKIPIF 1 < 0 与 SKIPIF 1 < 0 有公共顶点C， SKIPIF 1 < 0 为等边三角形，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ．
(1)如图1，当点E与点B重合时，连接AD，已知四边形ABDC的面积为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值；
(2)如图2， SKIPIF 1 < 0 ， A、E、D三点共线，连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，取 SKIPIF 1 < 0 中点M，连接 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 ；
(3)如图3， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 以C为旋转中心旋转，取 SKIPIF 1 < 0 中点F，当 SKIPIF 1 < 0 的值最小时，求 SKIPIF 1 < 0 的值．
【变式3】（2021·全国·九年级专题练习）如图1，在RT△ABC中，∠ACB＝90°，CB＝4，CA＝6，圆C的半径为2，点P为圆上一动点，连接AP，BP，求：
① SKIPIF 1 < 0 ，
② SKIPIF 1 < 0 ，
③ SKIPIF 1 < 0 ，
④ SKIPIF 1 < 0 的最小值．
考点4：胡不归模型
典例4：（2023秋·四川乐山·九年级统考期末）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，若D是 SKIPIF 1 < 0 边上的动点，则 SKIPIF 1 < 0 的最小值是（ ）
A．6B．8C．10D．12
【变式1】（2022春·全国·九年级专题练习）如图，在平面直角坐标系中，二次函数y＝x2﹣2x＋c的图象与x轴交于A、C两点，与y轴交于点B（0，﹣3），若P是x轴上一动点，点D（0，1）在y轴上，连接PD，则 SKIPIF 1 < 0 PD＋PC的最小值是（ ）
A．4B．2＋2 SKIPIF 1 < 0 C．2 SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式2】（2022·湖北武汉·校联考一模）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 的 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是圆 SKIPIF 1 < 0 的切线，且圆的直径 SKIPIF 1 < 0 在线段 SKIPIF 1 < 0 上，设点 SKIPIF 1 < 0 是线段 SKIPIF 1 < 0 上任意一点 SKIPIF 1 < 0 不含端点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为______．
【变式3】（2022秋·浙江·九年级专题练习）如图，四边形ABCD是菱形，AB＝8，且∠ABC＝60°，M为对角线BD（不含B点）上任意一点，则AM+ SKIPIF 1 < 0 BM的最小值为_____．
考点5：隐圆最值模型
典例5：（2023秋·浙江金华·九年级统考期末）如图，正方形 SKIPIF 1 < 0 的边长为4，点E是正方形 SKIPIF 1 < 0 内的动点，点P是 SKIPIF 1 < 0 边上的动点，且 SKIPIF 1 < 0 ．连结 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】（2022·山东泰安·统考中考真题）如图，四边形 SKIPIF 1 < 0 为矩形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．点P是线段 SKIPIF 1 < 0 上一动点，点M为线段 SKIPIF 1 < 0 上一点． SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式2】（2023秋·广东广州·九年级统考期末）如图，四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 是四边形 SKIPIF 1 < 0 内的一个动点，满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 面积的最小值为______．
【变式3】（2022春·全国·九年级专题练习）△ABC中，AB＝AC＝5，BC＝6，D是BC的中点，E为AB上一动点，点B关于DE的对称点 SKIPIF 1 < 0 在△ABC内（不含△ABC的边上），则BE长的范围为______．
巩固训练
一、单选题
1．（2022秋·安徽池州·九年级统考期末）如图， SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，点P为AC边上的动点，过点P作 SKIPIF 1 < 0 于点D，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．5D． SKIPIF 1 < 0
2．（2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末）如图， SKIPIF 1 < 0 为正方形 SKIPIF 1 < 0 边 SKIPIF 1 < 0 上一点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为对角线 SKIPIF 1 < 0 上一个动点，则 SKIPIF 1 < 0 的最小值为（ ）
A．5B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．10
3．（2022秋·浙江杭州·九年级杭州外国语学校校考开学考试）如图，在平面直角坐标系中，二次函数 SKIPIF 1 < 0 的图像与x轴交于A、C两点，与x轴交于点 SKIPIF 1 < 0 ，若P是x轴上一动点，点D的坐标为 SKIPIF 1 < 0 ，连接PD，则 SKIPIF 1 < 0 的最小值是（ ）
A．4B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4．（2022·河南·校联考三模）如图1，正方形 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点，点 SKIPIF 1 < 0 是对角线 SKIPIF 1 < 0 上的一个动点，设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，当点 SKIPIF 1 < 0 从 SKIPIF 1 < 0 向点 SKIPIF 1 < 0 运动时， SKIPIF 1 < 0 与 SKIPIF 1 < 0 的函数关系如图2所示，其中点 SKIPIF 1 < 0 是函数图象的最低点，则点 SKIPIF 1 < 0 的坐标是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2022秋·河北邢台·九年级统考期末）如图， SKIPIF 1 < 0 的半径是 SKIPIF 1 < 0 ，P是 SKIPIF 1 < 0 上一动点，A是 SKIPIF 1 < 0 内部一点，且 SKIPIF 1 < 0 ，则下列说法正确的是（ ）
①PA的最小值为 SKIPIF 1 < 0 ；②PA的最大值为 SKIPIF 1 < 0 ；③当 SKIPIF 1 < 0 时，△PAO是等腰直角三角形；④△PAO面积最大为 SKIPIF 1 < 0 ．
A．①③④B．①②④C．①②③D．②③④
7．（2022秋·北京海淀·九年级校考期中）如图，如图， SKIPIF 1 < 0 的半径为2，圆心 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 上的任意一点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 与x轴分别交于A，B两点，若点A、点B关于原点O对称，则 SKIPIF 1 < 0 的最小值为（ ）
A．3B．4C．5D．6
8．（2023春·九年级课时练习）如图，在Rt△ABC中，∠ACB＝90°，CB＝7，AC＝9，以C为圆心、3为半径作⊙C，P为⊙C上一动点，连接AP、BP，则 SKIPIF 1 < 0 AP＋BP的最小值为（ ）
A．7B．5 SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
9．（2022·福建厦门·福建省厦门集美中学校考一模）如图，在平面直角坐标系中，直线 SKIPIF 1 < 0 分别与x轴、y轴相交于点A、B，点E、F分别是正方形OACD的边OD、AC上的动点，且 SKIPIF 1 < 0 ，过原点O作 SKIPIF 1 < 0 ，垂足为H，连接HA、HB，则 SKIPIF 1 < 0 面积的最大值为（ ）
A． SKIPIF 1 < 0 B．12C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
10．（2023春·全国·八年级专题练习）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 是 SKIPIF 1 < 0 边上的动点，则 SKIPIF 1 < 0 的最小值（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
二、填空题
11．（2022秋·山东菏泽·九年级校考阶段练习）如图，在周长为 SKIPIF 1 < 0 的菱形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 为对角线 SKIPIF 1 < 0 上一动点，则 SKIPIF 1 < 0 的最小值为______．
12．（2023秋·山东东营·九年级校考期末）如图， SKIPIF 1 < 0 是⊙O的弦，点C在⊙O内， SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，若⊙O的半径是4，则 SKIPIF 1 < 0 长的最小值为______．
13．（2022春·全国·九年级专题练习）如图，在△ABC中，∠C＝90°，AC＝8，AB＝10，D是AC上一点，且CD＝3，E是BC边上一点，将△DCE沿DE折叠，使点C落在点F处，连接BF，则BF的最小值为_______．
14．（2023春·全国·八年级专题练习）如图，在平面直角坐标系中，直线l分别交x、y轴于B、C两点，点A、C的坐标分别为(3，0)、(0，﹣3)，且∠OCB＝60°，点P是直线l上一动点，连接AP，则 SKIPIF 1 < 0 的最小值是______．
15．（2022秋·浙江·九年级专题练习）如图，直线y＝x﹣3分别交x轴、y轴于B、A两点，点C（0，1）在y轴上，点P在x轴上运动，则 SKIPIF 1 < 0 PC＋PB的最小值为___．
三、解答题
16．（2023秋·江西宜春·八年级统考期末）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 边的垂直平分线 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点D，若 SKIPIF 1 < 0 ，
(1)求 SKIPIF 1 < 0 的长；
(2)若点P是直线 SKIPIF 1 < 0 上的动点，直接写出 SKIPIF 1 < 0 的最小值为_________．
17．（2022秋·河北保定·八年级统考期末）在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为 SKIPIF 1 < 0 延长线上一点，点 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的垂直平分线的交点，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)如图1，当 SKIPIF 1 < 0 时，则 SKIPIF 1 < 0 ______°；
(2)当 SKIPIF 1 < 0 时，
①如图2，连接 SKIPIF 1 < 0 ，判断 SKIPIF 1 < 0 的形状，并证明；
②如图3，直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 ． SKIPIF 1 < 0 为直线 SKIPIF 1 < 0 上一动点．当 SKIPIF 1 < 0 的值最大时，用等式表示 SKIPIF 1 < 0 ， SKIPIF 1 < 0 与 SKIPIF 1 < 0 之间的数量关系为______，并证明．
18．（2022春·全国·九年级专题练习）在平面直角坐标系， SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 经过 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上运动，求 SKIPIF 1 < 0 最小值．
19．（2021春·江苏苏州·八年级校考期中）定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别在边 SKIPIF 1 < 0 、 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的中点，且连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ．
(1)观察猜想
线段 SKIPIF 1 < 0 与 SKIPIF 1 < 0 ______填（“是”或“不是”）“等垂线段”．
(2) SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 按逆时针方向旋转到图2所示的位置，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，试判断 SKIPIF 1 < 0 与 SKIPIF 1 < 0 是否为“等垂线段”，并说明理由．
(3)拓展延伸
把 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 在平面内自由旋转，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，请直接写出 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的积的最大值．
20．（2022秋·山东济南·九年级山东师范大学第二附属中学校考阶段练习）如图1，抛物线 SKIPIF 1 < 0 与x轴交于点 SKIPIF 1 < 0 ，与y轴交于点B，在x轴上有一动点 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．
(1)求a的值和直线AB的函数表达式：
(2)设△PMN的周长为 SKIPIF 1 < 0 ，△AEN的周长为 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 求m的值．
(3)如图2，在（2）的条件下，将线段OE绕点O逆时针旋转得到 SKIPIF 1 < 0 ，旋转角为 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ），连接 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最小值．
21．（2022·湖南长沙·模拟预测）如图，抛物线 SKIPIF 1 < 0 （a为常数， SKIPIF 1 < 0 ）与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB＝OC．
(1)求a的值；
(2)点D是该抛物线的顶点，点P（m，n）是第三象限内抛物线上的一个点，分别连接BD、BC、CD、BP，当∠PBA＝∠CBD时，求m的值；
(3)点K为坐标平面内一点，DK＝2，点M为线段BK的中点，连接AM，当AM最大时，求点K的坐标．
22．（2022秋·江苏·九年级期中）问题情境：如图1，P是⊙O外的一点，直线PO分别交⊙O于点A，B，则PA是点P到⊙O上的点的最短距离．
（1）探究证明：如图2，在⊙O上任取一点C（不与点A，B重合），连接PC，OC．求证：PA＜PC．
（2）直接应用：如图3，在Rt△ABC中，∠ACB＝90°，AC＝BC＝3，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP，则AP的最小值是 ．
（3）构造运用：如图4，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A1MN，连接A1B，则A1B长度的最小值为 ．
（4）综合应用：如图5，平面直角坐标系中，分别以点A（﹣2，3），B（4，5）为圆心，以1，2为半径作⊙A，⊙B，M，N分别是⊙A，⊙B上的动点，P为x轴上的动点，直接写出PM+PN的最小值为 ．
23．（2021·全国·九年级专题练习）如图，△ABC中，∠BAC＝45°，AB＝6，AC＝4，P为平面内一点，求 SKIPIF 1 < 0 最小值