中考数学二轮复习考点提分特训专题09 三点共线问题（2份打包，原卷版+解析版）

这是一份中考数学二轮复习考点提分特训专题09 三点共线问题（2份打包，原卷版+解析版），文件包含中考数学二轮复习考点提分特训专题09三点共线问题原卷版doc、中考数学二轮复习考点提分特训专题09三点共线问题解析版doc等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。
【三点共线模型】
①函数模型：构建平面直角坐标系，求出三个点坐标，其中两个点构建一次函数模型，判断第三个点是否在函数图像上，满足则共线
②平角模型
如图，要证明A、B、C三点共线，可以选择一条过B点的直线PBQ，并连接AB、CB，证明∠ABP与∠CBP互为邻补角，即∠ABP+∠CBP=180°
③平行线模型
如图，要证明A、B、C三点共线，先证明AB∥DE，在证明BC∥DE
④垂线模型
如图，要证明A、B、C三点共线，先证明AC⊥MN，在证明A⊥MN
【三线共点模型】
①证明两条线的交点，在第三条直线上
②证明三条线中两条线的交点和另外两条线的交点是同一个
二、【考点类型】
考点1：三点共线
典例1：（2022秋·福建泉州·九年级校考阶段练习）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 绕点B按顺时针方向旋转得到 SKIPIF 1 < 0 ，当点E恰好落在线段 SKIPIF 1 < 0 上时，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的平分线 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点F，连接 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 的长；
(2)求证：C、E、F三点共线．
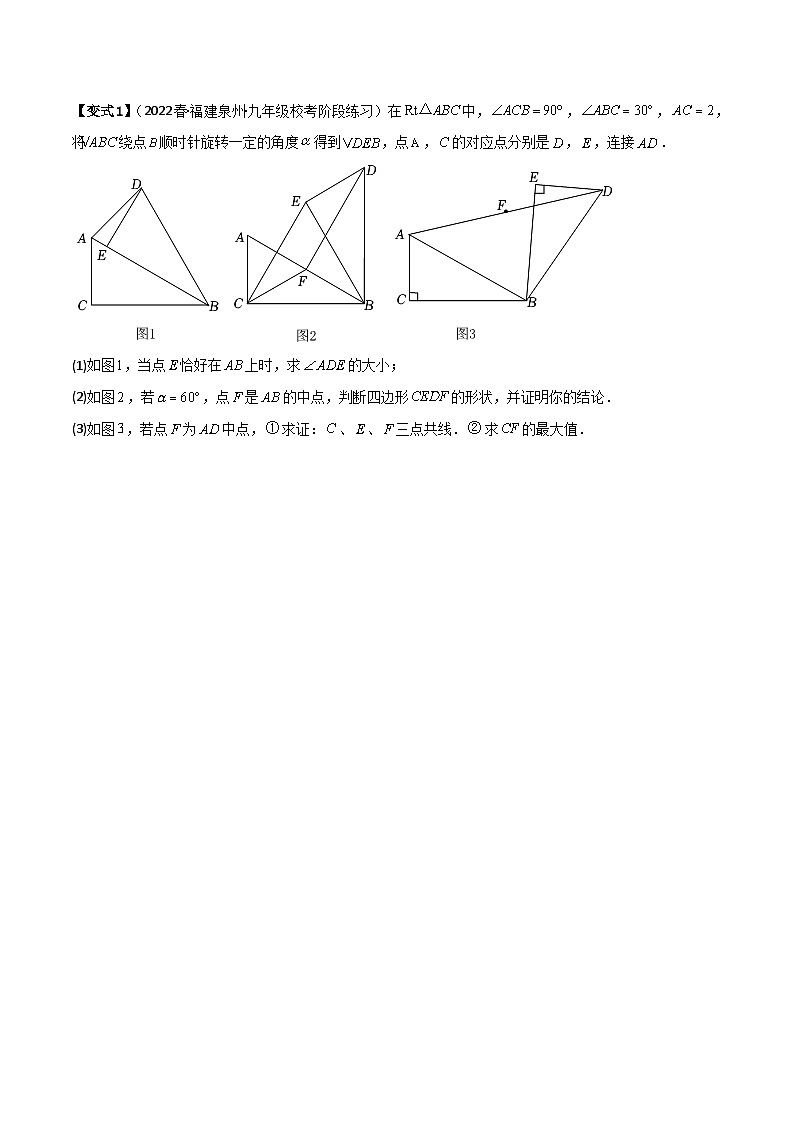
【变式1】（2022春·福建泉州·九年级校考阶段练习）在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 顺时针旋转一定的角度 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的对应点分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
(1)如图 SKIPIF 1 < 0 ，当点 SKIPIF 1 < 0 恰好在 SKIPIF 1 < 0 上时，求 SKIPIF 1 < 0 的大小；
(2)如图 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点，判断四边形 SKIPIF 1 < 0 的形状，并证明你的结论．
(3)如图 SKIPIF 1 < 0 ，若点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 中点， SKIPIF 1 < 0 求证： SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 三点共线． SKIPIF 1 < 0 求 SKIPIF 1 < 0 的最大值．
【变式2】（2021春·福建厦门·九年级校考阶段练习）抛物线C1：y＝﹣x2+2mx﹣m2+m+3的顶点为A，抛物线C2：y＝﹣（x+m+4）2﹣m﹣1的顶点为B，其中m≠﹣2，抛物线C1与C2相交于点P．
(1)当m＝1时，求抛物线C1的顶点坐标；
(2)已知点C（﹣2，1），求证：点A，B，C三点共线；
(3)设点P的纵坐标为q，求q的取值范围．
【变式3】（2022秋·福建福州·九年级统考期末）如图，已知矩形ABCD中， SKIPIF 1 < 0 于点E， SKIPIF 1 < 0 ．
(1)若 SKIPIF 1 < 0 ，求CE的长；
(2)设点C关于AD的对称点为F，求证：B，E，F三点共线．
考点2：三线共点
典例2：（2021·福建·统考中考真题）如图，已知线段 SKIPIF 1 < 0 ，垂足为a．
（1）求作四边形 SKIPIF 1 < 0 ，使得点B，D分别在射线 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；（要求：尺规作图，不写作法，保留作图痕迹）
（2）设P，Q分别为（1）中四边形 SKIPIF 1 < 0 的边 SKIPIF 1 < 0 的中点，求证：直线 SKIPIF 1 < 0 相交于同一点．
【变式1】（2020·福建·统考中考真题）如图， SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 外一点．
（1）求作四边形 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ；（要求：尺规作图，不写作法，保留作图痕迹）
（2）在（1）的四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 相交于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点分别为 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 三点在同一条直线上．
巩固训练
、单选题
1．（2023春·八年级课时练习）如图，正方形ABCD中，AB＝4，延长DC到点F（0＜CF＜4），在线段CB上截取点P，使得CP＝CF，连接BF、DP，再将△DCP沿直线DP折叠得到△DEP．下列结论：
①若延长DP，则DP⊥FB；
②若连接CE，则 SKIPIF 1 < 0 ；
③连接PF，当E、P、F三点共线时，CF＝4 SKIPIF 1 < 0 ﹣4；
④连接AE、AF、EF，若△AEF是等腰三角形，则CF＝4 SKIPIF 1 < 0 ﹣4；其中正确有（ ）
A．4个B．3个C．2个D．1个
2．（2023·全国·八年级专题练习）如图，在长方形ABCD中，AD SKIPIF 1 < 0 BC，AB SKIPIF 1 < 0 CD，E在AD上．AD＝m，AE＝n（m＞n＞0）．将长方形沿着BE折叠，A落在A′处，A'E交BC于点G，再将∠A′ED对折，点D落在直线A′E上的D′处，C落在C′处，折痕EF，F在BC上，若D、F、D′三点共线，则BF＝（ ）
A．m+ SKIPIF 1 < 0 nB． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．m﹣n
3．（2022秋·贵州黔西·九年级统考期末）如图，⊙O的半径为2 SKIPIF 1 < 0 ，PA，PB，CD分别切⊙O于点A，B，E，CD分别交PA，PB于点C，D，且P，E，O三点共线．若∠P＝60°，则CD的长为（ ）
A．4B．2 SKIPIF 1 < 0 C．3 SKIPIF 1 < 0 D．6
4．（2022秋·新疆乌鲁木齐·九年级校考期中）如图，Rt△ABC中，∠ACB=90°，∠B=60°，AB=6，将Rt△ABC绕点C顺时针旋转到Rt△A’B’C．当A’、B’、A三点共线时，AA’=（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2022秋·山东日照·八年级统考期中）如图，已知 SKIPIF 1 < 0 和 SKIPIF 1 < 0 都是等边三角形，且 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 三点共线． SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，连结 SKIPIF 1 < 0 ．以下五个结论：① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 ；④ SKIPIF 1 < 0 是等边三角形；⑤ SKIPIF 1 < 0 ．其中正确结论的有（ ）个
A．5B．4C．3D．2
二、填空题
6．（2023秋·浙江宁波·九年级统考期末）如图，在正方形 SKIPIF 1 < 0 中，点E在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，取 SKIPIF 1 < 0 中点F，过F作 SKIPIF 1 < 0 且使得 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 并延长，将 SKIPIF 1 < 0 绕点C旋转到 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 三点共线且 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ______．
7．（2023·全国·九年级专题练习）如图 SKIPIF 1 < 0 中， SKIPIF 1 < 0 与 SKIPIF 1 < 0 的平分线相交于H，过点H作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于E，交 SKIPIF 1 < 0 于F， SKIPIF 1 < 0 于D，以下四个结论① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ；③点H到 SKIPIF 1 < 0 各边的距离相等；④若B，H，D三点共线时， SKIPIF 1 < 0 一定为等腰三角形．其中正确结论的序号为 _____．
8．（2022春·福建龙岩·八年级校联考期中）已知矩形ABCD中，AB=8，BC=10，将△ABE沿BE对折，点A的对应点为 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 C，当E、 SKIPIF 1 < 0 、C恰好三点共线时，AE的值为____________
9．（2022春·福建泉州·八年级统考期末）如图，在 SKIPIF 1 < 0 中，E点是BD的中点，MN经过E点分别与AD、BC相交于点M、N．下列四个结论：
① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ；③A、C、E三点共线；④若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．其中正确的结论有____．（写出所有正确结论的序号）
10．（2022·福建·模拟预测）在平面直角坐标系 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 都在反比例函数 SKIPIF 1 < 0 的图象上，且 SKIPIF 1 < 0 ．现给出以下说法：
①若A，O，B三点共线，则 SKIPIF 1 < 0 ；
②若 SKIPIF 1 < 0 ，则A，O，B三点共线；
③线段OA长度的最小值是 SKIPIF 1 < 0 ；
④以A，O，B为顶点的三角形不可能是直角三角形．
其中正确的是__________．（写出所有正确说法的序号）
三、解答题
11．（2022秋·福建泉州·八年级统考期末）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)试说明 SKIPIF 1 < 0 与 SKIPIF 1 < 0 满足什么等量关系时，点D、点C、点E三点共线．
(2)连接 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于F点，若点F恰好是线段 SKIPIF 1 < 0 的中点，求证： SKIPIF 1 < 0 ．
12．（2023秋·河北邯郸·九年级统考期末）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，动点 SKIPIF 1 < 0 从点 SKIPIF 1 < 0 出发，沿 SKIPIF 1 < 0 以每秒5个单位长度的速度向终点 SKIPIF 1 < 0 运动，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，将线段 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 逆时针旋转90°得到线段 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．设点 SKIPIF 1 < 0 的运动时间为 SKIPIF 1 < 0 秒 SKIPIF 1 < 0 ．
(1)线段 SKIPIF 1 < 0 的长为__________，线段 SKIPIF 1 < 0 的长为__________（用含 SKIPIF 1 < 0 的代数式表示）；
(2)当点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 重合时，求 SKIPIF 1 < 0 的值；
(3)当 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 三点共线时，求 SKIPIF 1 < 0 的值；
(4)当 SKIPIF 1 < 0 为钝角三角形时，直接写出 SKIPIF 1 < 0 的取值范围．
13．（2022秋·福建泉州·八年级校考阶段练习）如图， SKIPIF 1 < 0 是等腰直角三角形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，D在线段 SKIPIF 1 < 0 上，E是线段 SKIPIF 1 < 0 的一点．现以 SKIPIF 1 < 0 为直角边，C为直角顶点，在 SKIPIF 1 < 0 的下方作等腰直角 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
(1)如图1，求证： SKIPIF 1 < 0 ．
(2)当A、E、F三点共线时，如图2，若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的长．
(3)如图3，若 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，当E运动到使得 SKIPIF 1 < 0 时，求 SKIPIF 1 < 0 的面积．
14．（2022秋·福建龙岩·九年级校联考期中）如图，在等腰直角 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 上一动点（不与点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 重合），将线段 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 逆时针方向旋转 SKIPIF 1 < 0 得到 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 ；
(2)①当点F运动到什么位置时，四边形 SKIPIF 1 < 0 是正方形？请你说明理由；
②当 SKIPIF 1 < 0 时，求证：点 SKIPIF 1 < 0 三点共线．
15．（2022秋·福建泉州·九年级校考阶段练习）已知直线y＝﹣2x＋4与交y轴于点A，交x轴于点B，直线CD经过点C（﹣1，0），交y轴于点D，若AB SKIPIF 1 < 0 CD．
(1)求直线CD的解析式；
(2)如图（1）若点E，F分别为AB，CD的中点，求证：E，O，F三点共线；
(3)如图（2）点M为线段BC上一动点（不与B，C重合），直线AM交CD于点N，求△ABM与△CNM面积和的最小值．