2024年中考第一次模拟考试题：数学（浙江卷）（参考答案及评分标准）

这是一份2024年中考第一次模拟考试题：数学（浙江卷）（参考答案及评分标准），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第Ⅰ卷
一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
第Ⅱ卷
二、填空题（本大题共6小题，每小题3分，共18分）
11．2
12．72
13．
14．
4
3
三、解答题（本大题共8个小题，共72分．解答应写出文字说明，证明过程或演算步骤）
17．【答案】（1）；（2）
【分析】本题考查了实数的运算以及解一元一次不等式；
（1）分别根据零指数幂的定义，绝对值的性质以及二次根式的性质，计算即可；
（2）不等式去括号，移项，合并同类项，化系数为1即可．
【详解】（1）原式
；·························································3分
（2），
去括号，得，
移项，得，
合并同类项，得．························································6分
18．【答案】错误步骤的序号为①，解法见详解．
【分析】本题考查检查解分式方程；错误步骤的序号为①，解方程去分母转化为整式方程，，进而解这个整式方程，最后检验，即可求解．
【详解】解：错误步骤的序号为①，························································1分
去分母得：
去括号得：
移项得：…③，
合并同类项得：…④，························································3分
检验：当时，，························································5分
∴是原分式方程的解．························································6分
19．【答案】(1)见解析
(2)，
(3)二，理由见解析
【分析】本题考查统计图分析，涉及中位数、加权平均数、众数，
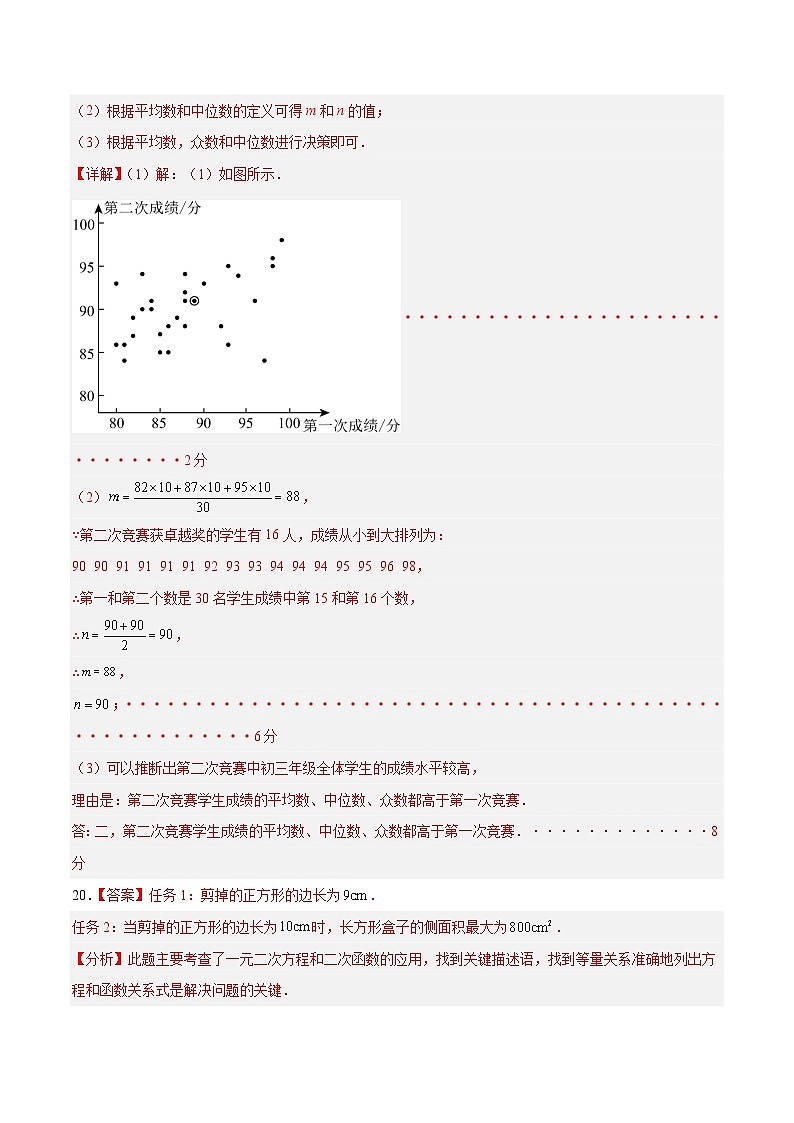
（1）根据这30名学生第一次竞赛成绩和第二次竞赛成绩得分情况统计图可得横坐标是89，纵坐标是90的点即代表小松同学的点；
（2）根据平均数和中位数的定义可得m和n的值；
（3）根据平均数，众数和中位数进行决策即可．
【详解】（1）解：（1）如图所示．
·······························2分
（2），
∵第二次竞赛获卓越奖的学生有16人，成绩从小到大排列为：
90 90 91 91 91 91 92 93 93 94 94 94 95 95 96 98，
∴第一和第二个数是30名学生成绩中第15和第16个数，
∴，
∴，；························································6分
（3）可以推断出第二次竞赛中初三年级全体学生的成绩水平较高，
理由是：第二次竞赛学生成绩的平均数、中位数、众数都高于第一次竞赛．
答：二，第二次竞赛学生成绩的平均数、中位数、众数都高于第一次竞赛．·············8分
20．【答案】任务1：剪掉的正方形的边长为．
任务2：当剪掉的正方形的边长为时，长方形盒子的侧面积最大为．
【分析】此题主要考查了一元二次方程和二次函数的应用，找到关键描述语，找到等量关系准确地列出方程和函数关系式是解决问题的关键．
任务1：假设剪掉的正方形的边长为，根据长方形盒子的底面积为，得方程，解所列方程并检验可得；
任务2：侧面积有最大值，设剪掉的正方形边长为，盒子的侧面积为，利用长方形盒子的侧面积为：得出即可．
【详解】解：任务1：设剪掉的正方形的边长为，
则，即，
解得（不合题意，舍去），，
答：剪掉的正方形的边长为．························································3分
任务2：侧面积有最大值．
理由如下：
设剪掉的小正方形的边长为，盒子的侧面积为，
则与的函数关系为：，
即，
即，························································6分
∴时，．························································8分
即当剪掉的正方形的边长为时，长方形盒子的侧面积最大为．
21．【答案】(1)支点C离桌面l的高度；
(2)面板上端E离桌面l的高度是增加了，增加了约
【分析】（1）作，先在求出的长，再计算即可得答案；
（2）分别求出时 和时，的长，相减即可．
【详解】（1）解：如下图，作，
，
，
，
，
支点C离桌面l的高度；···············································4分
（2）
，
，
当时，，························································5分
当时，，························································6分
，
面板上端E离桌面l的高度是增加了，增加了约．···································10分
【点睛】本题考查了解直角三角形的应用，解题的关键是作辅助线，构造直角三角形．
22．【答案】(1)
(2)
(3)
【分析】本题考查了相似三角形的判定与性质、正方形的性质等知识点，掌握相似三角形判定定理的内容是解题关键．
（1）证可得，结合即可求解；
（2）由可得，进一步可得，据此即可求解；
（3）由（1）可得，证得即可求解．
【详解】（1）解：由题意得：
∴
∴
即：
解得：························································2分
（2）解：∵，
∴
∴························································3分
由（1）可得：
∴
∴
∵，
∴························································5分
解得：························································6分
（3）解：由（1）得：
即：
解得：························································7分
∵，
∴
∴
即：
∴
整理得：························································8分
∵
∴，
又
∴
故：························································10分
23．【答案】(1)120
(2)2
(3)
(4)见解析，
【分析】本题主要考查了垂径定理在圆中的应用，最后一问由“共顶点，等线段”联想到旋转，是此题的突破口，同时，要注意顶角为的等腰三角形腰和底边比是固定值．
（1）由已知得到垂直平分，故得到，证明为等边三角形即可得到答案；
（2）由于直径，根据垂径定理可以得到是的中点，要求最大值即求最大值，当为直径时，有最大值，即可得到答案；
（3）根据垂径定理得到，证明，由（1）得，即可得到答案；
（4）将绕A点顺时针旋转至，得到，证明，过A作于G，则，根据勾股定理证明．
【详解】（1）解：连接，，
、，
，
，
，
，
，
，
，
的度数为；························································2分
（2）解：由题可知，为直径，且，
由垂径定理可得，，
连接，
是的中点，
，
当三点共线时，此时取得最大值，
且，
的最大值为；························································4分
（3）解：连接，
，
，
，
平分，
，
，
，
，
，
，
； ························································6分
（4）证明：由题可得，直径，
垂直平分，
如图4，连接，，则，
由（1）得，
将绕A点顺时针旋转至，
，
，，
四边形为圆内接四边形，
，
，
、D、P三点共线，
，························································7分
过A作于G，则，
，
在中，，
设，则，
，
，························································8分
，
，························································10分
为定值．
························································12分
24．【答案】(1)；
(2)①，；②的最小值为．
【分析】（1）将点、的坐标代入抛物线，利用待定系数法求得解析式；
（2）①由坐标求出解析式，然后根据四边形是平行四边形和得出，再分类讨论求得和的坐标；②求出解析式，交点为，再求出坐标，然后由两点间距离公式求出和长度，因为旋转不改变长度，所以长度不变，当旋转到轴上时，此时最短，所以此时等于，然后带入计算即可．
【详解】（1）解：①∵抛物线交轴于点和点，
∴将、坐标代入有，
解得
∴抛物线的表达式为；························································2分
（2）解：∵抛物线的表达式为，
∴，
设直线的解析式为
∵ ，，
∴
解得
∴直线的解析式为························································3分
∵为与轴交点，
∴，
∴，
∵四边形是平行四边形
∴且，且点在点下方，
∵且在轴上
∴，
∵，
∴，或，························································4分
若为，，
∵，故，
若为，，
∵，此时，矛盾，舍去
综上，；························································6分
②最小值为
如图，设的解析式为
∵抛物线交轴于点，
∴点的坐标为，
将点，、，的坐标代入得
解得
∴的解析式为
与相交于点
∴
解得
所以点的坐标为························································8分
设直线的解析式为
将点、的坐标代入直线的解析式得
解得
所以直线的解析式为························································9分
与相交于点
∴
解得，
∴点的坐标为························································10分
∴
，
∴，
当旋转到轴上时，此时最短，
∴，
∴．
故的最小值．························································12分
【点睛】本题考查了抛物线的综合运用，利用待定系数法求函数的解析式，找出相关点坐标，逐步分析求解是解题的关键．
1
2
3
4
5
6
7
8
9
10
D
B
C
B
D
C
A
B
B
A