

2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)03挑战压轴题(解答题一)(原卷版+解析)
展开1. (2023·安徽)为了解全市居民用户用电情况,某部门从居民用户中随机抽取100户进行月用电量(单位:kW•h)调查,按月用电量50~100,100~150,150~200,200~250,250~300,300~350进行分组,绘制频数分布直方图如下:
(1)求频数分布直方图中x的值;
(2)判断这100户居民用户月用电量数据的中位数在哪一组(直接写出结果);
(3)设各组居民用户月平均用电量如表:
根据上述信息,估计该市居民用户月用电量的平均数.
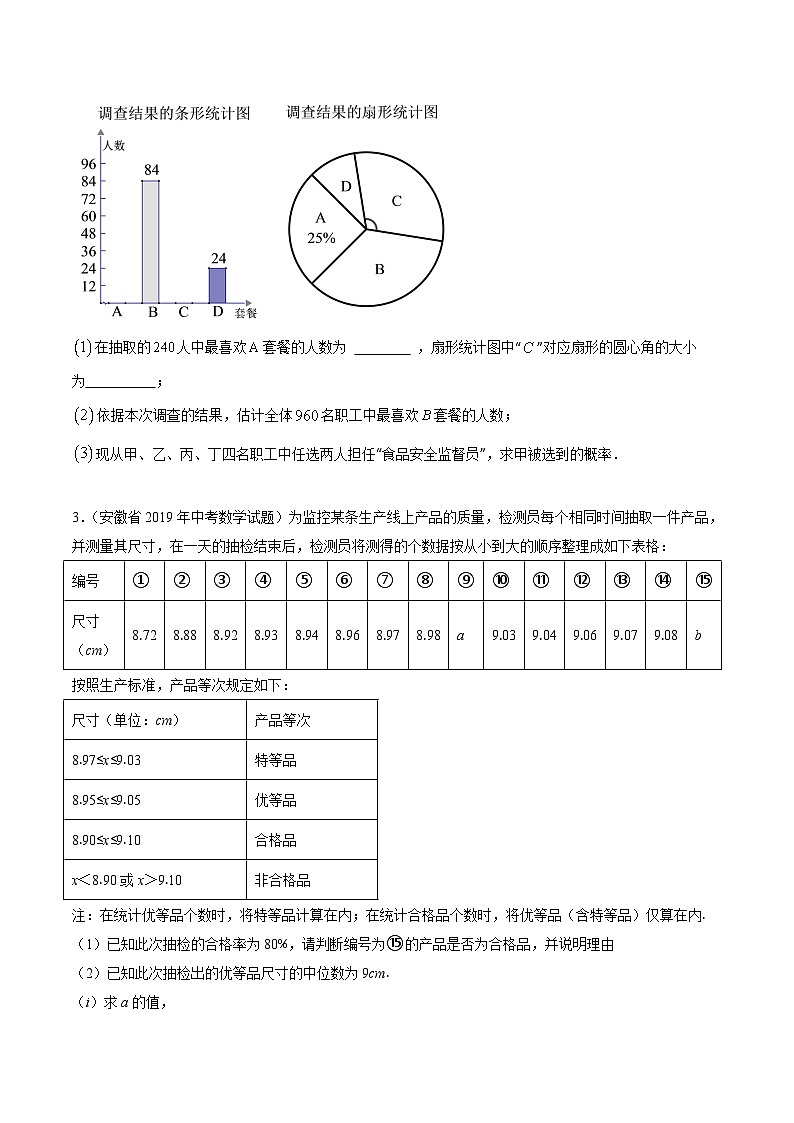
2.(安徽省2020年中考数学试题)某单位食堂为全体名职工提供了四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
在抽取的人中最喜欢套餐的人数为 ,扇形统计图中“”对应扇形的圆心角的大小为 ;
依据本次调查的结果,估计全体名职工中最喜欢套餐的人数;
现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
3.(安徽省2019年中考数学试题)为监控某条生产线上产品的质量,检测员每个相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的个数据按从小到大的顺序整理成如下表格:
按照生产标准,产品等次规定如下:
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)仅算在内.
(1)已知此次抽检的合格率为80%,请判断编号为⑮的产品是否为合格品,并说明理由
(2)已知此次抽检出的优等品尺寸的中位数为9cm.
(i)求a的值,
(ii)将这些优等品分成两组,一组尺寸大于9cm,另一组尺寸不大于9cm,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
4.(安徽省2018年中考数学试题)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
5. (2023·安徽)甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.
1. (2023·山东青岛·八年级期末)“冰雪之约,中国之邀”,第24届冬季奥林匹克运动会即将在中国举行.某国家队计划从甲、乙两名短道速滑运动员中选派一人参赛(均取整数,单位:秒)如下:
甲:37,41,38,40,39,37,39,42,37,40
乙:36,39,37,38,42,39,39,41,42,37
【整理数据】
甲成绩的扇形统计图(图1):
乙成绩的频数分布直方图(图2):
【分析数据】
请根据以上信息,完成下列问题:
(1)甲成绩的中位数a落在扇形统计图的 部分(填A,B,C);
(2)请补全乙成绩的频数分布直方图;
(3)表中b= ,c= ;
【做出决策】
(4)根据甲、乙两人10次选拔比赛的成绩,你认为该国家队应选派哪位运动员参赛?并说明理由.
2. (2023·安徽蚌埠·八年级期末)小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好
(1)小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是
(2)小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奧会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)
3. (2023·福建三明·七年级期末)为丰富校园文化生活,渲染学校的数学氛围,某校举办数学文化知识竞赛.将参赛学生的竞赛成绩按从高到低的顺序依次分为A,B, C, D, E五个等级.该校抽样调查了部分参赛学生的成绩,并制作成条形统计图(图1)和扇形统计图(图2), 但两幅统计图都受到一定程度的污损. 根据已知信息,解答如下问题:
(1)设该校这次调查共抽取了n名参赛学生的成绩,请写出n的值,并计算E等级在扇形统计图中对应扇形的圆心角的度数;
(2)请补全条形统计图;
(3)该校拟对竞赛成绩较优秀的同学进行一定的物质奖励,具体方案是:对获得B等级的参赛学生每人颁发金额10元的奖品,对获得A等级的参赛学生每人颁发金额20元的奖品,其他参赛学生不颁发奖品,所有参赛学生都颁发奖状,每张奖状价格2元.若参赛学生总数为200人,请根据抽样调查的数据估计本次竞赛该校需要颁发的奖品及奖状的总金额.
4. (2023·贵州遵义·九年级期末)为庆祝伟大的中国共产党建党100周年,我市某校组织学生开展以“学党史,感党恩”为主题的系列活动A:学红色历史,传承“红色基因”;B:读红色经典,领悟“红色精神”;C:讲红色故事续“红色血脉”;D:唱红色歌曲,重温“红色岁月”.学校为了解“学党史,感党恩”系列活动开展情况,随机抽取本校部分学生进行调查,并绘制出如下不完整的统计图.
(1)本次调查的总人数为 人,扇形统计图中B部分的圆心角是 度,请补全条形统计图;
(2)根据本次调查,估计该校800名学生中,参加活动A的学生有多少人?
(3)参加活动D的5名学生中,有两名男生和三名女生,若从这5名学生中随机抽取2名学生参加市级唱红歌比赛,请用画树状图或列表的方法,求正好抽到1男1女的概率.
5.(山西省太原市2021-2022学年七年级上学期期末数学试题)第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,将于2022年2月4日开幕,共设7个大项,15个分项,109个小项.学校从七年级同学中随机抽取若干名,组织了奥运知识竞答活动,将他们的成绩进行整理,得到如下不完整的频数分布表、频数分布直方图与扇形统计图.(满分为100分,将抽取的成绩分成A,B,C,D四组,每组含最大值不含最小值)
(1)本次知识竞答共抽取七年级同学__________名,D组成绩在扇形统计图中对应的圆心角为__________°;
(2)请将频数分布直方图与扇形统计图补充完整;
(3)学校将此次竞答活动的D组成绩记为优秀,已知该校初、高中共有学生2400名,小敏想根据七年级竞答活动的结果,估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.
1. (2023·山西晋中·七年级期末)某校为了做好课后延时服务,让“双减”政策落地生“花”,采取电子问卷(问卷如图所示)的方式随机调查了部分学生对课后延时服务的满意程度,所有问卷全部收回,并根据调查结果绘制成如下两幅不完整的统计图.请根据统计图提供的信息,解答下列问题:
(1)这次活动共调查了______人;
(2)请补全条形统计图;
(3)根据调查结果,估计该校1500名学生中对课后延时服务满意及非常满意的共有多少人?
(4)你对你所在学校的课后延时服务是否满意?答:______
A.非常满意 B.满意 C.一般 D.不满意
2. (2023·四川成都·九年级期末)2021年6月,天府国际机场正式通航.天府国际机场是4F级国际机场、国际航空枢纽、丝绸之路经济带中等级最高的航空港之一、成都国际航空枢纽的主枢纽.目前,市民出行到天府国际机场,通常可以选择地铁、专线大巴、自驾、出租车四种交通工具出行方式,小明通过调查统计附近居民的出行方式绘制了如下两幅不完整统计图.根据上述信息,解答下列问题:
(1)本次被调查的市民有 人;
(2)求出m的值,并补全条形统计图;
(3)小明和小亮分别乘坐交通工具去往天府国际机场,请用画树状图或列表的方法,求出两人恰好选到同一种交通工具的概率.
3. (2023·江苏徐州·二模)小丽在家备战体育中考,增强自身免疫力抗击疫情,每天晚上进行5组1分钟跳绳训练,10天成绩如下图.
(1)扇形统计图中a= .
(2)补全条形统计图.
(3)小丽的跳远成绩是跳绳平均成绩的90%,小丽的跳远成绩是多少分?(精确到个位)
4. (2023·福建·大同中学二模)为响应党中央关于打好精准扶贫攻坚战的号召,东部帮助西部进行扶贫产业开发,“食良品”是某市农产品商贸集团有限公司旗下的“消费扶贫”的电商平台,依托地理、集团专业等渠道的优势,基地直采,降低采购成本,全心全意为全市广大客户提供优质的食材,也解决了西部各地农副产品销售难的问题.目前,该平台为广大客户仅提供300元、500元、800元、1000元四种不同面额的提货券.随机抽查了其中100天的销售情况,整理统计后得到如下表一和表二:
表一
表二
(1)随机抽取一张提货券,面额不少于800元的概率是多少?
(2)哪种面额的提货券应多提供些?估计日均销售该面额的提货券多少张?
(3)估计月销售总额是多少元?(月以30天计算)
5. (2023·湖南·株洲市芦淞区教育教学研究指导中心模拟预测)我国农历年的岁首称为春节,是中华民族最隆重的传统节日,据记载,中华民族过春节已有4000多年的历史每年的除夕夜,对所有中国人而言,能和家人一起看年味浓浓的春晚是一件幸福的事情某社区就你对春晚的喜爱程度,进行了随机调查,对收集的信息进行统计,绘制了下面两幅尚不完整的统计图(图,图).
请根据图中信息,解答下列问题:
(1)本次调查的总人数为 人,扇形统计图中B所对应的扇形圆心角的度数为 ;
(2)补全条形统计图;
(3)若该社区共有2000人,估计该社区中很喜欢春晚的有多少人;
(4)在抽取的很喜欢春晚的5人中,刚好有3名男生,2名女生,从中随机抽取1人与大家分享“我与春晚的故事”,那么恰好抽到男生的概率是多少.
组别
50~100
100~150
150~200
200~250
250~300
300~350
月平均用电量(单位:kW•h)
75
125
175
225
275
325
编号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
⑪
⑫
⑬
⑭
⑮
尺寸(cm)
8.72
8.88
8.92
8.93
8.94
8.96
8.97
8.98
a
9.03
9.04
9.06
9.07
9.08
b
尺寸(单位:cm)
产品等次
8.97≤x≤9.03
特等品
8.95≤x≤9.05
优等品
8.90≤x≤9.10
合格品
x<8.90或x>9.10
非合格品
平均数
中位数
方差
甲
8
8
乙
8
8
2.2
丙
6
3
运动员
平均数
中位数
众数
方差
甲
39
a
37
c
乙
39
39
b
4
分组
频数
A:60~70
4
B:70~80
12
C:80~90
16
D:90~100
△
你对课后延时服务满意吗?(仅选一项)
.非常满意 .满意 .一般 .不满意
提货券每张面额(元)
300
500
800
1000
销售量(张)的百分比
30%
m%
18%
12%
日均销售量(张)
300
450
500
650
天数
25
30
35
10
2024年中考数学冲刺 挑战压轴题专题汇编(安徽考卷)
03挑战压轴题(解答题一)
1. (2023·安徽)为了解全市居民用户用电情况,某部门从居民用户中随机抽取100户进行月用电量(单位:kW•h)调查,按月用电量50~100,100~150,150~200,200~250,250~300,300~350进行分组,绘制频数分布直方图如下:
(1)求频数分布直方图中x的值;
(2)判断这100户居民用户月用电量数据的中位数在哪一组(直接写出结果);
(3)设各组居民用户月平均用电量如表:
根据上述信息,估计该市居民用户月用电量的平均数.
【答案】(1)22;(2);(3)
【解析】
【分析】
(1)利用100减去其它各组的频数即可求解;
(2)中位数是第50和51两个数的平均数,第50和51两个数都位于月用电量150~200的范围内,由此即可解答;
(3)利用加权平均数的计算公式即可解答.
【详解】
(1)
(2)∵中位数是第50和51两个数的平均数,第50和51两个数都位于月用电量150~200的范围内,
∴这100户居民用户月用电量数据的中位数在月用电量150~200的范围内;
(3)设月用电量为y,
答:该市居民用户月用电量的平均数约为.
【点睛】
本题考查了频数分布直方图、中位数及加权平均数的知识,正确识图,熟练运用中位数及加权平均数的计算方法是解决问题的关键.
2.(安徽省2020年中考数学试题)某单位食堂为全体名职工提供了四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
在抽取的人中最喜欢套餐的人数为 ,扇形统计图中“”对应扇形的圆心角的大小为 ;
依据本次调查的结果,估计全体名职工中最喜欢套餐的人数;
现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
【答案】(1)60,108°;(2)336;(3)
【分析】
(1)用最喜欢套餐的人数对应的百分比乘以总人数即可,先求出最喜欢C套餐的人数,然后用最喜欢C套餐的人数占总人数的比值乘以360°即可求出答案;
(2)先求出最喜欢B套餐的人数对应的百分比,然后乘以960即可;
(3)用列举法列出所有等可能的情况,然后找出甲被选到的情况即可求出概率.
【详解】
(1)最喜欢套餐的人数=25%×240=60(人),
最喜欢C套餐的人数=240-60-84-24=72(人),
扇形统计图中“”对应扇形的圆心角为:360°×=108°,
故答案为:60,108°;
(2)最喜欢B套餐的人数对应的百分比为:×100%=35%,
估计全体名职工中最喜欢套餐的人数为:960×35%=336(人);
(3)由题意可得,从甲、乙、丙、丁四名职工中任选两人,总共有6种不同的结果,每种结果发生的可能性相同,列举如下:甲乙,甲丙,甲丁,乙丙,乙丁,丙丁,
其中甲被选到的情况有甲乙,甲丙,甲丁3种,
故所求概率P==.
【点睛】
本题考查了条形统计图和扇形统计图,用样本估计总体,用列举法求概率,由图表获取正确的信息是解题关键.
3.(安徽省2019年中考数学试题)为监控某条生产线上产品的质量,检测员每个相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的个数据按从小到大的顺序整理成如下表格:
按照生产标准,产品等次规定如下:
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)仅算在内.
(1)已知此次抽检的合格率为80%,请判断编号为⑮的产品是否为合格品,并说明理由
(2)已知此次抽检出的优等品尺寸的中位数为9cm.
(i)求a的值,
(ii)将这些优等品分成两组,一组尺寸大于9cm,另一组尺寸不大于9cm,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
【答案】(1)不合格,见解析;(2)(i)a=9.02,(ii).
【分析】
(1)判断出非合格品有3个,其中①②是非合格品,即可确定⑮是非合格品;
(2)(i)判断出符合优等品尺寸的编号是⑥~⑪,根据中位数是9可得正中间两个数据的平均数是9,可求出a的值;
(ii)优等品尺寸大于9cm的有⑨⑩⑪,小于9cm的有⑥⑦⑧,其中特等品为⑦⑧⑨⑩,画树状图即可.
【详解】
解:(1)不合格.因为15×80%=12,不合格的有15-12=3个,给出的数据只有①②两个不合格;
(2)(i)优等品有⑥~⑪,中位数在⑧8.98,⑨a之间,∴,解得a=9.02
(ii)大于9cm的有⑨⑩⑪,小于9cm的有⑥⑦⑧,其中特等品为⑦⑧⑨⑩
画树状图为:
共有九种等可能的情况,其中抽到两种产品都是特等品的情况有4种,
∴抽到两种产品都是特等品的概率P=
【点睛】
本题主要考查了中位数、树状图或列表法求概率,用到的知识点为:概率=所求情况数与总情况数之比.
4.(安徽省2018年中考数学试题)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
【答案】(1)50,30%;(2)不能,理由见解析;(3)P=
【详解】
【分析】(1)由直方图可知59.5~69.5分数段有5人,由扇形统计图可知这一分数段人占10%,据此可得选手总数,然后求出89.5~99.5这一分数段所占的百分比,用1减去其他分数段的百分比即可得到分数段69.5~79.5所占的百分比;
(2)观察可知79.5~99.5这一分数段的人数占了60%,据此即可判断出该选手是否获奖;
(3)画树状图得到所有可能的情况,再找出符合条件的情况后,用概率公式进行求解即可.
【详解】(1)本次比赛选手共有(2+3)÷10%=50(人),
“89.5~99.5”这一组人数占百分比为:(8+4)÷50×100%=24%,
所以“69.5~79.5”这一组人数占总人数的百分比为:1-10%-24%-36%=30%,
故答案为50,30%;
(2)不能;由统计图知,79.5~89.5和89.5~99.5两组占参赛选手60%,而78<79.5,所以他不能获奖;
(3)由题意得树状图如下
由树状图知,共有12种等可能结果,其中恰好选中1男1女的共有8种结果,故P==.
【点睛】本题考查了直方图、扇形图、概率,结合统计图找到必要信息进行解题是关键.
5. (2023·安徽)甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.
【答案】解:(1)2,6
(2)甲运动员的成绩最稳定.
(3)甲、乙相邻出场的概率.
【解析】
【详解】
试题分析:(1)根据中位数和方差的定义求解;(2)根据方差的意义求解;(3)用列举法求概率.
试题解析:解:(1)
(2)因为,所以,这说明甲运动员的成绩最稳定.
(3)三人的出场顺序有(甲乙丙),(甲丙乙),(乙甲丙),(乙丙甲),(丙甲乙),(丙乙甲)共6种,且每一种结果出现的可能性相等,其中,甲、乙相邻出场的结果有(甲乙丙),(乙甲丙),(丙甲乙),(丙乙甲)共4种,所以甲、乙相邻出场的概率.
考点: 中位数、方差的求法,方差的意义,求等可能事件的概率.
1. (2023·山东青岛·八年级期末)“冰雪之约,中国之邀”,第24届冬季奥林匹克运动会即将在中国举行.某国家队计划从甲、乙两名短道速滑运动员中选派一人参赛(均取整数,单位:秒)如下:
甲:37,41,38,40,39,37,39,42,37,40
乙:36,39,37,38,42,39,39,41,42,37
【整理数据】
甲成绩的扇形统计图(图1):
乙成绩的频数分布直方图(图2):
【分析数据】
请根据以上信息,完成下列问题:
(1)甲成绩的中位数a落在扇形统计图的 部分(填A,B,C);
(2)请补全乙成绩的频数分布直方图;
(3)表中b= ,c= ;
【做出决策】
(4)根据甲、乙两人10次选拔比赛的成绩,你认为该国家队应选派哪位运动员参赛?并说明理由.
【答案】(1)B
(2)补全频数分布直方图见解析
(3)39,2.8
(4)选甲,理由见解析
【解析】
【分析】
(1)根据中位数的定义求出a的值,再结合扇形统计图即可确定其落在哪部分;
(2)根据所给数据可求出乙的成绩在37.5-39.5的频数为4,即可补全分布直方图;
(3)根据众数的定义即可求出b的值,根据方差的计算公式即可求出c的值.
(4)甲和乙成绩的平均值相同,判断其方差即可,方差越小,数据波动越小,成绩越稳定,甲的方差小,选甲即可.
(1)
将甲的成绩从小到大排列为:37,37,37,38,39,39,40,40,41,42
∴中位数,
根据扇形统计图可知甲成绩的中位数a落在扇形统计图的B部分.
故答案为:B.
(2)
根据所给数据可知乙的成绩在37.5-39.5的频数为4,
∴补全乙成绩的频数分布直方图如下:
(3)
乙成绩39秒出现了3次,最多
∴.
根据方法的计算公式得:
∴.
故答案为:39,2.8.
(4)
∵,
∴甲的成绩比乙更稳定,应选甲.
【点睛】
本题考查频数分布直方图,扇形统计图,中位数、众数、平均数以及方差,理解中位数、众数、平均数以及方差的定义,掌握中位数、众数以及方差的求法是解答本题的关键.
2. (2023·安徽蚌埠·八年级期末)小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好
(1)小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是
(2)小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奧会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)
【答案】(1)
(2)
【解析】
【分析】
(1)根据概率公式求解即可;
(2)列树状图得到所有的等可能性的结果数,然后找到符合题意的结果数,最后根据概率公式求解即可.
(1)
解:∵有四张邮票,冰墩墩的邮票有一张,
∴小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是,
故答案为:;
(2)
解:列树状图如下所示:
由树状图可知一共有12种等可能性的结果数,其中抽到的两张邮票恰好是“冬奥会会徽”和“冬奧会吉祥物冰墩墩”的结果数有2种,
∴抽到的两张邮票恰好是“冬奥会会徽”和“冬奧会吉祥物冰墩墩”的概率.
【点睛】
本题主要考查了概率公式和树状图或列表法求解概率,熟知相关知识是解题的关键.
3. (2023·福建三明·七年级期末)为丰富校园文化生活,渲染学校的数学氛围,某校举办数学文化知识竞赛.将参赛学生的竞赛成绩按从高到低的顺序依次分为A,B, C, D, E五个等级.该校抽样调查了部分参赛学生的成绩,并制作成条形统计图(图1)和扇形统计图(图2), 但两幅统计图都受到一定程度的污损. 根据已知信息,解答如下问题:
(1)设该校这次调查共抽取了n名参赛学生的成绩,请写出n的值,并计算E等级在扇形统计图中对应扇形的圆心角的度数;
(2)请补全条形统计图;
(3)该校拟对竞赛成绩较优秀的同学进行一定的物质奖励,具体方案是:对获得B等级的参赛学生每人颁发金额10元的奖品,对获得A等级的参赛学生每人颁发金额20元的奖品,其他参赛学生不颁发奖品,所有参赛学生都颁发奖状,每张奖状价格2元.若参赛学生总数为200人,请根据抽样调查的数据估计本次竞赛该校需要颁发的奖品及奖状的总金额.
【答案】(1),E 等级在扇形统计图中对应扇形的圆心角为;
(2)见解析;
(3)次竞赛该校需要颁发的奖品和奖状的总金额为元
【解析】
【分析】
(1)根据条形统计图中A等级的人数及扇形统计图中A等级人数所占的百分比即可求得n的值;由条形统计图中E等级的人数及求得的总人数即可求得E等级所占的百分比,则可求得E等级在扇形统计图中对应扇形的圆心角的度数;
(2)由扇形统计图及(1)中所求的数据即可求得D等级所占的百分比,从而可求得B、C、D三个等级所占的人数,然后可补全条形统计图;
(3)估算出分别获得A、B两个等级的人数,则可求得需要颁发的奖品金额;再计算出颁发奖状的金额,即可求得本次竞赛该校需要颁发的奖品和奖状的总金额.
(1)
根据条形统计图和扇形统计图可得,(人).
E等级所占的百分比为:
则 E 等级在扇形统计图中对应扇形的圆心角为.
(2)
由扇形统计图及(1)可知,D等级所占的百分比为:
B等级的人数为:(人),C等级的人数为:(人),D等级的人数为:(人)
补全后的条形统计图如下图:
(3)
根据样本估计总体的思想,可估计获得A等级的参赛学生人数为(人),
获得B等级的参赛学生人数为(人).
则需要颁发的奖品金额为(元),
颁发的奖状金额为(元),
所以本次竞赛该校需要颁发的奖品和奖状的总金额为(元)
【点睛】
本题是条形统计图与扇形统计图的综合,考查了条形统计图与扇形统计图,求扇形统计图中扇形的圆心角,用样本估计总体等知识,善于从统计图中获取信息是解题的关键.
4. (2023·贵州遵义·九年级期末)为庆祝伟大的中国共产党建党100周年,我市某校组织学生开展以“学党史,感党恩”为主题的系列活动A:学红色历史,传承“红色基因”;B:读红色经典,领悟“红色精神”;C:讲红色故事续“红色血脉”;D:唱红色歌曲,重温“红色岁月”.学校为了解“学党史,感党恩”系列活动开展情况,随机抽取本校部分学生进行调查,并绘制出如下不完整的统计图.
(1)本次调查的总人数为 人,扇形统计图中B部分的圆心角是 度,请补全条形统计图;
(2)根据本次调查,估计该校800名学生中,参加活动A的学生有多少人?
(3)参加活动D的5名学生中,有两名男生和三名女生,若从这5名学生中随机抽取2名学生参加市级唱红歌比赛,请用画树状图或列表的方法,求正好抽到1男1女的概率.
【答案】(1)50;;统计图见解析
(2)参加活动A的学生有192人
(3)
【解析】
【分析】
(1)由D项目人数及其所占百分比可得总人数,用360°乘以B项目人数所占比例可得其对应圆心角度数,总人数减去A、B、D人数求出C的人数即可补全图形;
(2)用总人数乘以样本中A项目人数所占比例即可;
(3)列表求概率,共有20种等可能的结果,刚好抽到1男1女的有12种情况,再利用概率公式即可求得答案.
(1)
本次调查的总人数为5÷10%=50(人),扇形统计图中B部分的圆心角是360°×=108°,
C活动项目的人数为50−(12+15+5)=18(人),
补全图形如下:
故答案为:50、108;
(2)
800×=192(人),
答:估计该校800名学生中,参加活动A的学生有192人;
(3)
列表如下:设B表示男生,G表示女生
共有20种等可能的结果,其中正好抽到1男1女的结果数为12,
所以正好抽到1男1女的概率为
【点睛】
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
5.(山西省太原市2021-2022学年七年级上学期期末数学试题)第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,将于2022年2月4日开幕,共设7个大项,15个分项,109个小项.学校从七年级同学中随机抽取若干名,组织了奥运知识竞答活动,将他们的成绩进行整理,得到如下不完整的频数分布表、频数分布直方图与扇形统计图.(满分为100分,将抽取的成绩分成A,B,C,D四组,每组含最大值不含最小值)
(1)本次知识竞答共抽取七年级同学__________名,D组成绩在扇形统计图中对应的圆心角为__________°;
(2)请将频数分布直方图与扇形统计图补充完整;
(3)学校将此次竞答活动的D组成绩记为优秀,已知该校初、高中共有学生2400名,小敏想根据七年级竞答活动的结果,估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.
【答案】(1)40,72
(2)见解析
(3)不合理.理由:此次“知识竞答”活动随机抽查的是七年级学生,产生的样本对于全校学生而言不具有代表性(合理即可)
【解析】
【分析】
(1)由B组人数及其所占百分比可得七年级学生的总人数,根据四个分组人数之和等于总人数求出D组人数,用360°乘以D组人数所占比例即可
(2)先求出A、D组人数占被调查的学生人数比例即可
(3)根据样本估计总体时,样本需要具有代表性求解即可
(1)
解:本次知识竞答共抽取七年级同学(名),
则D组的人数为40-(4+12+16)=8(名)
∴D组成绩在扇形统计图中对应的圆心角为
故答案为40、72
(2)
A组人数所占百分比为,D组人数所占百分比为,
补全图形如下:
(3)
不合理.理由:此次“知识竞答”活动随机抽查的是七年级学生,产生的样本对于全校学生而言不具有代表性(合理即可)
【点睛】
本题考查了统计数据的梳理,计算时需注意,扇形圆心角度数=部分占总体的百分数×360°,熟练运用相关知识点是解题关键
1. (2023·山西晋中·七年级期末)某校为了做好课后延时服务,让“双减”政策落地生“花”,采取电子问卷(问卷如图所示)的方式随机调查了部分学生对课后延时服务的满意程度,所有问卷全部收回,并根据调查结果绘制成如下两幅不完整的统计图.请根据统计图提供的信息,解答下列问题:
(1)这次活动共调查了______人;
(2)请补全条形统计图;
(3)根据调查结果,估计该校1500名学生中对课后延时服务满意及非常满意的共有多少人?
(4)你对你所在学校的课后延时服务是否满意?答:______
A.非常满意 B.满意 C.一般 D.不满意
【答案】(1)200
(2)补全条形统计图见解析
(3)估计该校1500名学生中对课后延时服务满意及非常满意的共有900人
(4)A,B,C,D四个选项都正确(答案不唯一)
【解析】
【分析】
(1)根据A的人数与占比计算总人数即可;
(2)作差求出C的人数,然后补全条形统计图即可;
(3)计算总人数与满意及非常满意的占比的乘积即可;
(4)根据个人的观点进行选择即可.
(1)
解:由题意知这次活动调查的总人数为人
故答案为:200.
(2)
解:C有人
补全统计图如下:
(3)
解:由题意得(人)
∴根据调查结果,估计该校1500名学生中对课后延时服务满意及非常满意的共有900人.
(4)
解:根据个人观点进行选择即可
故选B(答案不唯一).
【点睛】
本题考查了条形统计图与扇形统计图,样本估计总体等知识.解题的关键在于从图中获取正确的信息.
2. (2023·四川成都·九年级期末)2021年6月,天府国际机场正式通航.天府国际机场是4F级国际机场、国际航空枢纽、丝绸之路经济带中等级最高的航空港之一、成都国际航空枢纽的主枢纽.目前,市民出行到天府国际机场,通常可以选择地铁、专线大巴、自驾、出租车四种交通工具出行方式,小明通过调查统计附近居民的出行方式绘制了如下两幅不完整统计图.根据上述信息,解答下列问题:
(1)本次被调查的市民有 人;
(2)求出m的值,并补全条形统计图;
(3)小明和小亮分别乘坐交通工具去往天府国际机场,请用画树状图或列表的方法,求出两人恰好选到同一种交通工具的概率.
【答案】(1)80
(2)m=60,图形见解析
(3)
【解析】
【分析】
(1)由选择专线大巴交通工具出行方式的人数除以所占百分比即可;
(2)求出选择地铁交通工具出行方式的人数所占的百分比得出m的值,再求出选择自驾交通工具出行方式的人数,补全条形统计图即可;
(3)画树状图,共有16种等可能的结果,其中小明和小亮两人恰好选到同一种交通工具的结果有4种,再由概率公式求解即可.
(1)
解:由条形统计图知:选择“专线大巴”交通工具出行方式的人数有12人,
由扇形统计图知:选择“专线大巴”交通工具占总人数的百分比为15%,
故总人数=12÷15%=80(人).
(2)
解:由题意可知:m%=48÷80×100%=60%,
∴m的值为60;
∵选择出租车交通工具出行方式的人数为:80×10%=8(人),
∴选择自驾交通工具出行方式的人数为:80-48-12-8=12(人),
补全条形统计图如下:
(3)
解:把地铁、专线大巴、自驾、出租车四种交通工具出行方式分别记为A、B、C、D,
画树状图如下:
共有16种等可能的结果,其中小明和小亮两人恰好选到同一种交通工具的结果有4种,
∴小明和小亮两人恰好选到同一种交通工具的概率为.
【点睛】
此题考查的是用列表法或树状图法求概率、条形统计图、扇形统计图.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;同时要注意将条形统计图与扇形统计图结合来看,获取有用信息.
3. (2023·江苏徐州·二模)小丽在家备战体育中考,增强自身免疫力抗击疫情,每天晚上进行5组1分钟跳绳训练,10天成绩如下图.
(1)扇形统计图中a= .
(2)补全条形统计图.
(3)小丽的跳远成绩是跳绳平均成绩的90%,小丽的跳远成绩是多少分?(精确到个位)
【答案】(1)46
(2)见解析
(3)8分
【解析】
【分析】
(1)用1分别减去6分,7分,8分,9分所占的百分率即可;
(2)用“10分”的人数它所占的比例求出总天数,再乘“8分”所占的比例即可求出“8分”的天数,再补全条形统计图即可;
(3)求出跳绳平均成绩,再乘即可.
(1)
解:,
,
故答案为:46;
(2)
总组数为:(组),
“8分”的天数为:(组),
补全条形统计图如下:
(3)
小丽的跳绳平均成绩为:(分),
小丽的跳远成绩是:(分).
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
4. (2023·福建·大同中学二模)为响应党中央关于打好精准扶贫攻坚战的号召,东部帮助西部进行扶贫产业开发,“食良品”是某市农产品商贸集团有限公司旗下的“消费扶贫”的电商平台,依托地理、集团专业等渠道的优势,基地直采,降低采购成本,全心全意为全市广大客户提供优质的食材,也解决了西部各地农副产品销售难的问题.目前,该平台为广大客户仅提供300元、500元、800元、1000元四种不同面额的提货券.随机抽查了其中100天的销售情况,整理统计后得到如下表一和表二:
表一
表二
(1)随机抽取一张提货券,面额不少于800元的概率是多少?
(2)哪种面额的提货券应多提供些?估计日均销售该面额的提货券多少张?
(3)估计月销售总额是多少元?(月以30天计算)
【答案】(1)面额不少于800元的概率为30%
(2)该面额的提货券约为180张
(3)月销售总额为7479000元
【解析】
【分析】
(1)从表一中读取数据即可得到答案.
(2)由销售量的百分比总和为1,可得m的值,对比各百分比大小可得答案;求出日均销售提货券的数量,按照该提货券占的百分比,可得答案.
(3)根据加权平均数可得平均每张提货券的销售金额,根据销售总额=平均每张提货券的销售金额×日均销售提货券的数量×时间,可得答案.
(1)
解:面额不少于800元的概率为:18%+12%=30%.
(2)
解: m=100﹣30﹣18﹣12=40,
故500的提货券应多提供些.
平均每天销售提货券的数量为: (张).
其中该面额的提货券约为:450×40%=180(张).
(3)
解:平均每张提货券的销售金额为:300×30%+500×40%+800×18%+1000×12%=554(元).
故月销售总额为:30×450×554=7479000(元).
【点睛】
本题考查统计概率方面知识的综合运用,正确读取并理解图表信息是解题的关键.
5. (2023·湖南·株洲市芦淞区教育教学研究指导中心模拟预测)我国农历年的岁首称为春节,是中华民族最隆重的传统节日,据记载,中华民族过春节已有4000多年的历史每年的除夕夜,对所有中国人而言,能和家人一起看年味浓浓的春晚是一件幸福的事情某社区就你对春晚的喜爱程度,进行了随机调查,对收集的信息进行统计,绘制了下面两幅尚不完整的统计图(图,图).
请根据图中信息,解答下列问题:
(1)本次调查的总人数为 人,扇形统计图中B所对应的扇形圆心角的度数为 ;
(2)补全条形统计图;
(3)若该社区共有2000人,估计该社区中很喜欢春晚的有多少人;
(4)在抽取的很喜欢春晚的5人中,刚好有3名男生,2名女生,从中随机抽取1人与大家分享“我与春晚的故事”,那么恰好抽到男生的概率是多少.
【答案】(1)50,72°
(2)见解析
(3)200
(4)
【解析】
【分析】
(1)用很喜欢春晚的人数除以很喜欢春晚的人数所占的百分比,可得到总人数;再用喜欢春晚的人数所占的百分比乘以360°,即可求解;
(2)根据题意,补全图形即可求解;
(3)用2000乘以喜欢春晚的人数所占的百分比,即可求解;
(4)用男生的人数除以5,即可求解.
(1)
解:本次调查的总人数为;
喜欢春晚的人数为,
所以扇形统计图中B所对应的扇形圆心角的度数为;
故答案为:50,72°;
(2)
解:补全条形统计图如解图所示;
(3)
解:人,
答:估计该社区中很喜欢春晚的有200人;
(4)
解:很喜欢春晚的有5人,其中有3名男生,随机抽取一名,恰好抽到男生的概率是.
【点睛】
本题主要考查了扇形统计图和条形统计图,求概率,用样本估计总体,明确题意,从统计图中获取准确信息是解题的关键.
组别
50~100
100~150
150~200
200~250
250~300
300~350
月平均用电量(单位:kW•h)
75
125
175
225
275
325
编号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
⑪
⑫
⑬
⑭
⑮
尺寸(cm)
8.72
8.88
8.92
8.93
8.94
8.96
8.97
8.98
a
9.03
9.04
9.06
9.07
9.08
b
尺寸(单位:cm)
产品等次
8.97≤x≤9.03
特等品
8.95≤x≤9.05
优等品
8.90≤x≤9.10
合格品
x<8.90或x>9.10
非合格品
平均数
中位数
方差
甲
8
8
乙
8
8
2.2
丙
6
3
平均数
中位数
方差
甲
2
乙
丙
6
运动员
平均数
中位数
众数
方差
甲
39
a
37
c
乙
39
39
b
4
--
--
--
--
--
分组
频数
A:60~70
4
B:70~80
12
C:80~90
16
D:90~100
△
你对课后延时服务满意吗?(仅选一项)
.非常满意 .满意 .一般 .不满意
提货券每张面额(元)
300
500
800
1000
销售量(张)的百分比
30%
m%
18%
12%
日均销售量(张)
300
450
500
650
天数
25
30
35
10
2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)02挑战压轴题(填空题)(原卷版+解析): 这是一份2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)02挑战压轴题(填空题)(原卷版+解析),共29页。
2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)01挑战压轴题(选择题)(原卷版+解析): 这是一份2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)01挑战压轴题(选择题)(原卷版+解析),共26页。
2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)05挑战压轴题(解答题三)(原卷版+解析): 这是一份2024年中考数学冲刺挑战压轴题专题汇编(安徽卷)05挑战压轴题(解答题三)(原卷版+解析),共51页。试卷主要包含了如图1,已知正方形,点为边的中点.等内容,欢迎下载使用。












