

- 北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)专题09线段上的动点问题(原卷版+解析) 试卷 0 次下载
- 北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期中考试B卷压轴题考点训练(一)(原卷版+解析) 试卷 0 次下载
- 北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(一)(原卷版+解析) 试卷 0 次下载
- 北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(三)(原卷版+解析) 试卷 0 次下载
- 北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(二)(原卷版+解析) 试卷 0 次下载
北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期中考试B卷压轴题考点训练(二)(原卷版+解析)
展开3.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a,2的对面数字为b,那么a+b的值为_____.
4.有理数a,b,c在数轴上的对应点如图所示,化简:|b|-|c+b|+|b-a|=________.
5.已知数轴上的点A,B表示的数分别为,4,P为数轴上任意一点,表示的数为x,若点P到点A,B的距离之和为7,则x的值为 _____.
6.在一次数学活动课上,某数学老师将1~10共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲、乙、丙、丁、戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:11;乙:4;丙:15;丁:8;戊:17,则丙同学手里拿的卡片的数字是_________.
7.如图所示的图形是按一定规律排列的.
则第个图形中的个数为__________.
9.如图,红黄绿三块一样大的正方形纸片放在一个正方形盒内,它们之间互相重叠.已知露在外面的部分中,红色的面积是20,黄色的面积是13,绿色的面积是11,则正方形盒子的面积为_____________.
10.如图①是一个小正方体的侧面展开图,小正方体从如图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,这时小正方体朝上面的字是__________.
11.2021年国庆档电影《长津湖》以抗美援朝为背景,讲述了中国人民志愿军在极端严酷惨烈的环境下,凭借钢铁意志最终取得了长津湖战役的胜利,该电影也再次扻起了全民爱国热潮,国安民才安,有国才有家!据猫眼数据,截止10月8日,《长津湖》累计票房超过60亿,成为2021年全球票房冠军!该电影9月30日在莱芜的票房为6.7万元,接下来国庆假期7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房).
(1)国庆假期7天中,10月4日的票房收入是______万元;
(2)国庆假期7天中,票房收入最多的一天是10月______日;
(3)国庆假期7天中,求票房收入最多的一天比最少的一天多多少万元?
12.已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B”看成“2A+B”,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=,b=,求(2)中式子的值.
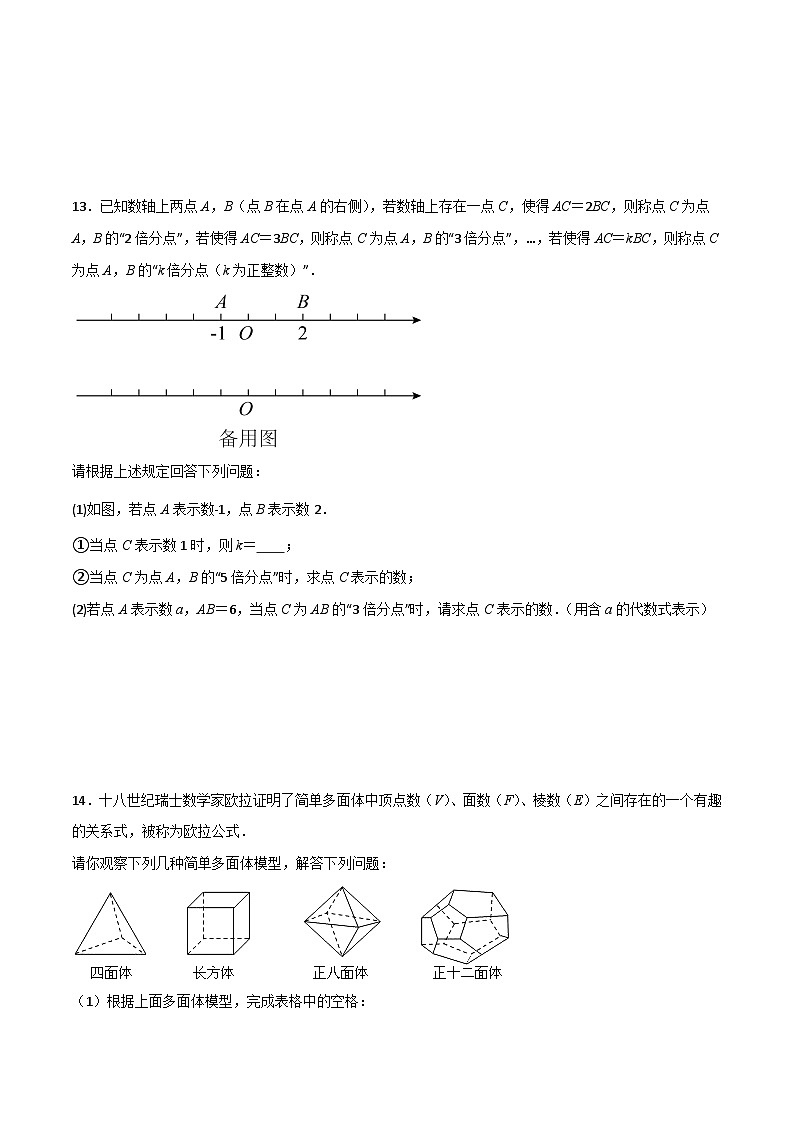
13.已知数轴上两点A,B(点B在点A的右侧),若数轴上存在一点C,使得AC=2BC,则称点C为点A,B的“2倍分点”,若使得AC=3BC,则称点C为点A,B的“3倍分点”,…,若使得AC=kBC,则称点C为点A,B的“k倍分点(k为正整数)”.
请根据上述规定回答下列问题:
(1)如图,若点A表示数﹣1,点B表示数2.
①当点C表示数1时,则k= ;
②当点C为点A,B的“5倍分点”时,求点C表示的数;
(2)若点A表示数a,AB=6,当点C为AB的“3倍分点”时,请求点C表示的数.(用含a的代数式表示)
14.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
15.如图,点 A 在数轴上对应的数为a,点B 对应的数为b,点O 为数轴原点,已知|a+5|+(a+b+1)2=0.
(1)求 a、b 的值;
(2)若数轴上有一点 C,且 AC+BC=15,求点 C 在数轴上对应的数;
(3)若点 P 从点 A 出发沿数轴的正方向以每秒 2 个单位长度的速度运动,同时点 Q 从点 B 出发沿数轴的负方向以每秒 4 个单位长度的速度运动,运动时间为t 秒,则数轴上点 P 表示的数为______,点 Q 表示的数为________.(用含 t 的代数式表示);当 OP=2OQ 时,t的值为_____________.(在横线上直接填写答案)
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
票房(万元)
+7.6
+2.7
+2.5
+4.7
+2
-0.6
-13.8
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
期中考试B卷压轴题考点训练(二)
1.已知代数式x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2合并同类项后不含x3,x2项,则2a+3b的值 _____.
【答案】
【详解】解:x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2
=x4+(a+5)x3+(3﹣7﹣b)x2+6x﹣2,
∵x4+ax3+3x2+5x3﹣7x2﹣bx2+6x﹣2,合并同类项后不含x3和x2项,
∴a+5=0,3﹣7﹣b=0,
解得:a=﹣5,b=﹣4,
∴2a+3b=2×(﹣5)+3×(﹣4)=﹣22.
故答案为:﹣22.
2.若实数,满足,,则________.
【答案】−1或5
【详解】解:∵|a|=2,
∴a=±2,
当a=2时,|4−b|=1−2=−1,此时b不存在;
当a=−2时,|4−b|=3,
∴4−b=3或4−b=−3,
即b=1或b=7,
当a=−2,b=1时,a+b=−1;
当a=−2,b=7时,a+b=5.
故答案为:−1或5.
3.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a,2的对面数字为b,那么a+b的值为_____.
【答案】7
【详解】一个正方体已知1,4,6,第二个正方体已知1,2,3,第三个正方体已知2,5,6,且不同的面上写的数字各不相同,可求得1的对面数字为5,6的对面数字为3,2的对面数字为4
∴a+b=7
故答案为:7.
4.有理数a,b,c在数轴上的对应点如图所示,化简:|b|-|c+b|+|b-a|=________.
【答案】a-b+c
【详解】先根据各点在数轴上的位置判断出其符号,再去绝对值符号,合并同类项即可,即可由图可知,c<b<0<a,可求c+b<0,b-a<0,因此原式=-b+c+b+a-b=a+c-b.
故答案为a+c-b.
5.已知数轴上的点A,B表示的数分别为,4,P为数轴上任意一点,表示的数为x,若点P到点A,B的距离之和为7,则x的值为 _____.
【答案】或4.5
【详解】解:根据题意得:|x+2|+|x-4|=7,
当x<-2时,化简得:-x-2-x+4=7,解得:x=-2.5;
当-2≤x<4时,化简得:x+2-x+4=7,无解;
当x≥4时,化简得:x+2+x-4=7,解得:x=4.5,
综上,x的值为-2.5或4.5.
故答案为:-2.5或4.5.
6.在一次数学活动课上,某数学老师将1~10共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲、乙、丙、丁、戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,写出的结果依次是:甲:11;乙:4;丙:15;丁:8;戊:17,则丙同学手里拿的卡片的数字是_________.
【答案】5和10
【详解】解:由题意可知,一共十张卡片十个数,五个人每人两张卡片,
∴每人手里的数字不重复.
由甲:11,可知甲手中的数字可能是1和10,2和9,3和8,4和7,5和6;
由乙:4,可知乙手中的数字只有1和3;
由丙:15,可知丙手中的数字可能是5和10,7和8,6和9;
由丁:8,可知丁手中的数字可能是1和7,2和6,3和5;
由戊:17,可知戊手中的数字可能是7和10,8和9;
∴丁只能是2和6,甲只能是4和7,丙只能是5和10,戊只能是8和9.
故答案为:5和10.
7.如图所示的图形是按一定规律排列的.
则第个图形中的个数为__________.
【答案】
【详解】解:∵第一个图形中圆的个数:4=3×1+1,
第二个图形中圆的个数:7=3×2+1,
第三个图形中圆的个数:10=3×3+1,
第四个图形中圆的个数:13=3×4+1,
……
∴第n个图形中圆的个数为:3n +1 ,
故答案为:..
8.如图,在数轴上点表示,现将点 沿轴做如下移动:第一次点向左移动个单位长度到达点,第二次将点 向右移动个单位长度到达点,第三次将点向左移动个单位长度到达点,按照这种移动规律移动下去,则线段的长度是 .
【答案】42.
【详解】根据观察可知,奇数点在A点的左侧,且根据A1=-2=1+(-3),A3=-5=1+(-3)×2,
故A13=1+(-3)×7=-20;
偶数点在A点的右侧,且根据A2=4=1+3,A4= -5+12=7=1+3×2,
故A14=1+7×3=22;故A13和A14的长度为|22-(-20)|=42.
9.如图,红黄绿三块一样大的正方形纸片放在一个正方形盒内,它们之间互相重叠.已知露在外面的部分中,红色的面积是20,黄色的面积是13,绿色的面积是11,则正方形盒子的面积为_____________.
【答案】
【详解】解∶如图,将黄色部分向左平移,
∴黄色部分减少的面积为绿色部分增加的面积,
∵红黄绿三块一样大的正方形,整个盒子为正方形,
∴平移后,黄色部分与绿色部分面积相等,
∴平移前,黄色的面积是13,绿色的面积是11,
∴平移后黄色部分与绿色部分面积为∶ ( 13+11) 2=12,
设大正方形边长为b,红色部分边长为a,则黄色部分和绿色部分的长为a,宽为b-a,
∴,∴,∴,∴,故答案为∶.
10.如图①是一个小正方体的侧面展开图,小正方体从如图②所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,这时小正方体朝上面的字是__________.
【答案】路
【详解】解:由图1可知:“国”和“兴”是对面,“梦”和“中”是对面,“复”和“路”是对面,
再由图2可知,1、2、3、4、5分别对应的面是“兴”、“梦”、“路”、“国”、“复”,
所以第5格朝上的字是“路”.
所以答案是路.
11.2021年国庆档电影《长津湖》以抗美援朝为背景,讲述了中国人民志愿军在极端严酷惨烈的环境下,凭借钢铁意志最终取得了长津湖战役的胜利,该电影也再次扻起了全民爱国热潮,国安民才安,有国才有家!据猫眼数据,截止10月8日,《长津湖》累计票房超过60亿,成为2021年全球票房冠军!该电影9月30日在莱芜的票房为6.7万元,接下来国庆假期7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房).
(1)国庆假期7天中,10月4日的票房收入是______万元;
(2)国庆假期7天中,票房收入最多的一天是10月______日;
(3)国庆假期7天中,求票房收入最多的一天比最少的一天多多少万元?
【答案】(1)24.2;(2)5;(3)票房收入最多的一天比最少的一天多14.4万元
【解析】(1)
解: 10月4日的票房收入是:6.7+7.6+2.7+2.5+4.7=24.2(万元),
故答案为:24.2;
(2)
解:10月1日票房收入为:6.7+7.6=14.3(万元),
10月2日票房收入为:14.3+2.7=17(万元),
10月3日票房收入为:17+2.5=19.5(万元),
10月4日票房收入为:19.5+4.7=24.2(万元),
10月5日票房收入为:24.2+2=26.2(万元),
10月6日票房收入为:26.2−0.6=25.6(万元),
10月7日票房收入为:25.6−13.8=11.8(万元),
故国庆假期7天中,票房收入最多的一天是10月5日.
故答案为:5;
(3)
解:26.2−11.8=14.4(万元),
故票房收入最多的一天比最少的一天多14.4万元.
12.已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B”看成“2A+B”,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=,b=,求(2)中式子的值.
【答案】(1)﹣2a2b+ab2+2abc;(2) 8a2b﹣5ab2;(3)对,0.
【详解】解:(1)∵2A+B=4a2b﹣3ab2+4abc,
∴B=4a2b﹣3ab2+4abc-2A=4a2b-3ab2+4abc-2(3a2b-2ab2+abc)
=4a2b-3ab2+4abc-6a2b+4ab2-2abc=-2a2b+ab2+2abc;
(2)2A-B=2(3a2b-2ab2+abc)-(-2a2b+ab2+2abc)
=6a2b-4ab2+2abc+2a2b-ab2-2abc=8a2b-5ab2;
(3)对,由(2)化简的结果可知与c无关,
将a=,b=代入,得8a2b-5ab2=8××-5××=0.
13.已知数轴上两点A,B(点B在点A的右侧),若数轴上存在一点C,使得AC=2BC,则称点C为点A,B的“2倍分点”,若使得AC=3BC,则称点C为点A,B的“3倍分点”,…,若使得AC=kBC,则称点C为点A,B的“k倍分点(k为正整数)”.
请根据上述规定回答下列问题:
(1)如图,若点A表示数﹣1,点B表示数2.
①当点C表示数1时,则k= ;
②当点C为点A,B的“5倍分点”时,求点C表示的数;
(2)若点A表示数a,AB=6,当点C为AB的“3倍分点”时,请求点C表示的数.(用含a的代数式表示)
【答案】(1)①2; ②C表示的数为或;(2)a+或a+9
【解析】(1)①k=[1﹣(﹣1)]÷(2﹣1)=2;
故答案为:2;
②设点C表示的数为x;
若点C在线段AB之间,则AC=x+1,BC=2﹣x,
∵AC=5BC,
∴x+1=5(2﹣x),
∴;
若点C在线段AB延长线上,则AC=x+1,BC=x﹣2,
∵AC=5BC,
∴x+1=5(x﹣2),
∴.
综上所述,C表示的数为或.
(2)
6×=,
6÷=9,
故C表示的数为a+或a+9.
故答案为:a+或a+9..
14.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
【答案】(1)填表见解析,V+F-E=2;(2)20;(3)14
【详解】解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为:V+F-E=2;
(2)由题意得:F-8+F-30=2,解得F=20;
(3)∵有24个顶点,每个顶点处都有3条棱,两点确定一条直线;
∴共有24×3÷2=36条棱,
那么24+F-36=2,解得F=14,
∴x+y=14.
15.如图,点 A 在数轴上对应的数为a,点B 对应的数为b,点O 为数轴原点,已知|a+5|+(a+b+1)2=0.
(1)求 a、b 的值;
(2)若数轴上有一点 C,且 AC+BC=15,求点 C 在数轴上对应的数;
(3)若点 P 从点 A 出发沿数轴的正方向以每秒 2 个单位长度的速度运动,同时点 Q 从点 B 出发沿数轴的负方向以每秒 4 个单位长度的速度运动,运动时间为t 秒,则数轴上点 P 表示的数为______,点 Q 表示的数为________.(用含 t 的代数式表示);当 OP=2OQ 时,t的值为_____________.(在横线上直接填写答案)
【答案】(1)a=﹣5,b=4
(2)﹣8或7
(3)﹣5+2t,4﹣4t,或
【解析】(1)
∵|a+5|+(a+b+1)2=0,
∴a+5=0,a+b+1=0,
∴a=﹣5,b=4.
(2)
设点C在数轴上对应的数为x,
∵AB=4﹣(﹣5)=9,
∴点C在点A的左侧或点B的右侧,如图1所示.
若点C在点A左侧,则AC=﹣5﹣x,BC=4﹣x,
∴AC+BC=﹣5﹣x+4﹣x=﹣1﹣2x=15,
解得:x=﹣8;
若点C在点B右侧,则AC=x﹣(﹣5)=x+5,BC=x﹣4,
∴AC+BC=x+5+x﹣4=15,
解得:x=7.
∴点C在数轴上对应的数为﹣8或7.
(3)
由题意可得: P 表示的数为﹣5+2t,点 Q 表示的数为4﹣4t,
OP=|5﹣2t|,OQ=|4﹣4t|,如图2所示.
∵OP=2OQ,
∴|5﹣2t|=2|4﹣4t|,
解得:t1,t2.
∴当OP=2OQ时,t的值为或.
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
票房(万元)
+7.6
+2.7
+2.5
+4.7
+2
-0.6
-13.8
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
6
长方体
8
6
12
正八面体
6
8
12
正十二面体
20
12
30
北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(四)(原卷版+解析): 这是一份北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(四)(原卷版+解析),共10页。试卷主要包含了若,则______,对于数轴上给定的两点A,B等内容,欢迎下载使用。
北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(五)(原卷版+解析): 这是一份北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(五)(原卷版+解析),共12页。试卷主要包含了先化简,再求值,【阅读理解】等内容,欢迎下载使用。
北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(二)(原卷版+解析): 这是一份北师大版2023-2024学年七年级数学上册压轴题攻略(成都专用)期末考试B卷压轴题考点训练(二)(原卷版+解析),共12页。试卷主要包含了如图,,为其内部一条射线等内容,欢迎下载使用。












