北师大版七年级上册2.1 有理数课后复习题

这是一份北师大版七年级上册2.1 有理数课后复习题，共29页。试卷主要包含了km等内容，欢迎下载使用。

一．选择题（本大题共10小题，每小题3分，满分30分）
1．（2022•黔东南州）下列说法中，正确的是（ ）
A．2与﹣2互为倒数B．2与12互为相反数
C．0的相反数是0D．2的绝对值是﹣2
2．（2021秋•滕州市月考）下列说法中正确的有（ ）个．①0是整数，也是正数：②﹣123是负分数；③3.2是正小数，不是正分数；④自然数一定是正数；⑤负分数一定是负有理数；⑥非负数就是正数和零．
A．0B．1C．2D．3
3．（2022春•东台市月考）某种细胞开始分裂时有两个，1小时后分裂成4个并死去一个，2小时后分裂成6个并死去一个，3小时后分裂成10个并死去一个，按此规律，8小时后细胞存活的个数是（ ）
A．253B．255C．257D．259
4．（2021秋•新华区校级期中）若a，b互为相反数，且ab≠0，c、d互为倒数，|m|＝2，则（a+b）2021+（ba）3﹣3cd+2m的值（ ）
A．0B．0或﹣8C．﹣2成6D．2或﹣6
5．（2020秋•江阴市校级月考）电子跳蚤落在数轴上的某点K0，第一步从K0向左跳1个单位到K1，第二步由K1向右跳2个单位到K2，第三步由K2向左跳3个单位到K3，第四步由K3跳4个单位到K4，…，按以上规律跳了100步时，电子跳蚤落在数轴上的点K100所表示的数恰是30，则电子跳蚤的初始位置K0点所表示的数为（ ）
A．﹣26B．﹣20C．﹣30D．30
6．（2022•钟山县模拟）计算：1+12+122+123+124+⋯⋯+1299+12100结果是（ ）
A．1−12100B．1−12101C．2−12100D．2−12101
7．（2022春•岳麓区校级月考）在一次数学活动课上，某数学老师在4张同样的纸片上各写了一个正整数，从中随机取2张，并将它们上面的数相加，重复这样做，每次所得的和都是5，6，7，8中的一个数，并且这4个数都能取到，根据以上信息，下列判断正确的是（ ）
A．四个正整数中最小的是1
B．四个正整数中最大的是8
C．四个正整数中有两个是2
D．四个正整数中一定有3
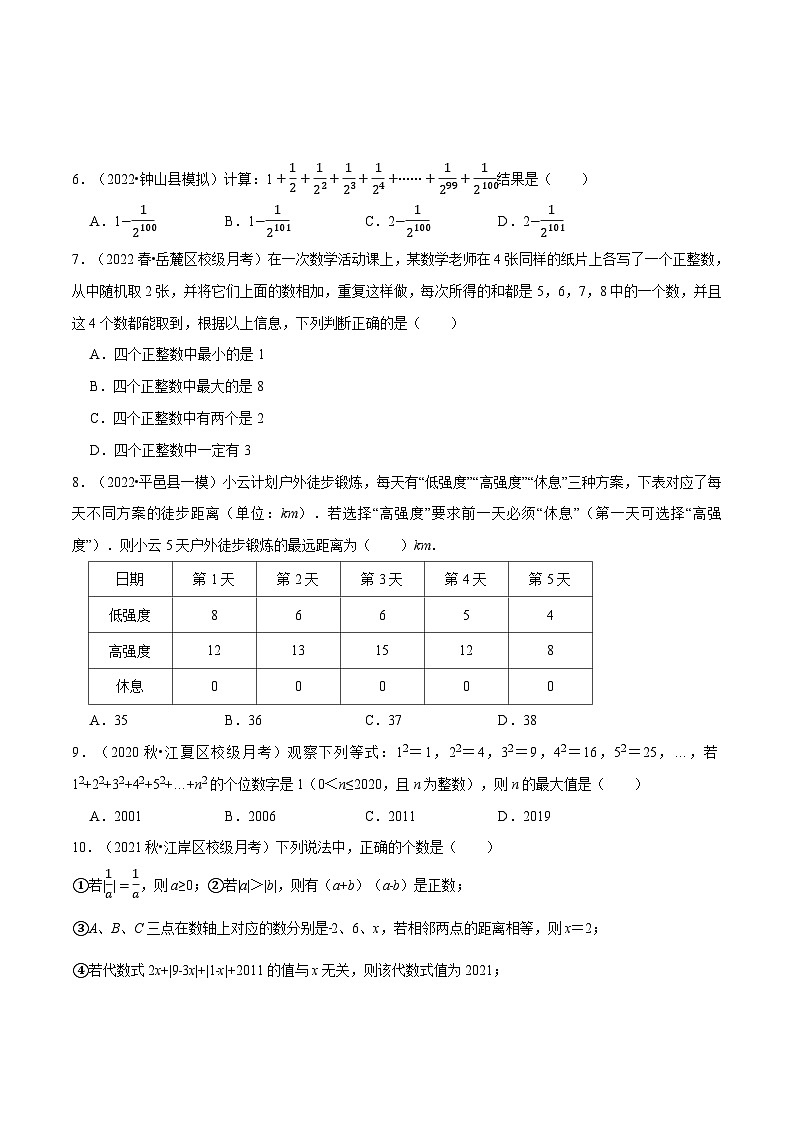
8．（2022•平邑县一模）小云计划户外徒步锻炼，每天有“低强度”“高强度”“休息”三种方案，下表对应了每天不同方案的徒步距离（单位：km）．若选择“高强度”要求前一天必须“休息”（第一天可选择“高强度”）．则小云5天户外徒步锻炼的最远距离为（ ）km．
A．35B．36C．37D．38
9．（2020秋•江夏区校级月考）观察下列等式：12＝1，22＝4，32＝9，42＝16，52＝25，…，若12+22+32+42+52+…+n2的个位数字是1（0＜n≤2020，且n为整数），则n的最大值是（ ）
A．2001B．2006C．2011D．2019
10．（2021秋•江岸区校级月考）下列说法中，正确的个数是（ ）
①若|1a|=1a，则a≥0；②若|a|＞|b|，则有（a+b）（a﹣b）是正数；
③A、B、C三点在数轴上对应的数分别是﹣2、6、x，若相邻两点的距离相等，则x＝2；
④若代数式2x+|9﹣3x|+|1﹣x|+2011的值与x无关，则该代数式值为2021；
⑤a+b+c＝0，abc＜0，则b+c|a|+a+c|b|+a+b|c|的值为±1．
A．1个B．2个C．3个D．4个
二．填空题（本大题共5小题，每小题3分，满分15分）
11．（2021秋•东城区期末）现把2021个连续整数1，2，3…2021的每个数的前面任意填上“+”号或者“﹣”号，然后将它们相加，则所得的结果绝对值的最小值为 ．
12．（2021秋•公安县期末）小聪在纸上画了一条数轴后，折叠纸面，使数轴上表示﹣2的点与表示5的点重合，若数轴上A，B两点之间的距离为10，且A，B两点经上述折叠后重合，则B点表示的数为 ．
13．（2021秋•大田县期中）三个整数a，b，c满足a＜b＜c，且a+b+c＝0．若|a|＜10，则|a|+|b|+|c|的最大值为 ．
14．（2021春•杨浦区校级期末）已知a，b，c为整数，且|a﹣b|2021+|c﹣a|2020＝1，则|a﹣b|+|b﹣c|+|c﹣a|＝ ．
15．（2020秋•鄞州区期末）已知整数a，b，c，d的绝对值均小于5，且满足1000a+100b2+10c3+d4＝2021，则abcd的值为 ．
三．解答题（本大题共8小题，满分55分）
16．（8分）（2021秋•随县期末）计算：
①﹣2×3﹣|﹣4|； ②﹣32+（−12）×（﹣8）+（﹣6）2；
③（134−78−712）×（﹣117）； ④8÷（﹣6）﹣[﹣3+116×（−27）]．
17．（4分）（2022春•南岸区校级月考）我国约有9600000平方千米的土地，平均1平方千米的土地一年从太阳得到的能量相当于燃烧150000吨煤所产生的能量．
（1）一年内我国土地从太阳得到的能量相当于燃烧多少吨煤所产生的能量？
（2）若1吨煤大约可以发出8000度电，那么（1）中的煤大约发出多少度电？（结果用科学记数法表示）
18．（6分）（2021秋•邹城市期中）已知下列各有理数：a，b，c的大小关系为a＜﹣1＜b＜0＜1＜c．
（1）画出数轴，在数轴上标出这些数表示的点；
（2）在横线上填上合适的符号（＞或＜或＝）：
①a+c b+c；②a﹣c a﹣b；③ab ac；④ab ac；
（3）化简：|a+b|﹣|b﹣c|﹣|1﹣c|．
19．（6分）（2022•义安区模拟）观察以下算式：
①1×11×5=18×(1+31×5)；
②2×35×9=18×(1+35×9)；
③3×59×13=18×(1+39×13)．
（1）请写出第④个算式： ．
（2）请用n（n是正整数）表示出第n个算式，并计算1×11×5+2×35×9+3×59×13+⋯+9×1733×37+10×1937×41．
20．（6分）（2021秋•汝阳县期末）某批发商于上周日买进某产品10000kg，每千克2.4元，进入批发市场后共占5个摊位，每个摊位最多能容纳2000kg该品种的产品，每个摊位的市场管理价为每天20元．如表为本周内该产品每天的批发价格比前一天的涨跌情况．（涨记为正，跌记为负，上周日当天的售价刚好为每千克2.4元）
（1）星期四该产品价格为每千克多少元？
（2）本周内该产品的最高价格为每千克多少元？最低价格为每千克多少元？
（3）该批发商在销售过程中采用逐步减少摊位个数（每天减少一个）的方法来降低成本，增加收益，请你帮他算一算，这样他在本周的买卖中共赚了多少钱？
21．（8分）（2021秋•嘉鱼县期末）数轴是一个非常重要的数学工具，它使数和数轴上的点建立起一一对应的关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．我们知道|4|＝|4﹣0|，它的几何意义是数轴上表示4的点与原点（即表示0的点）之间的距离，又如式子|7﹣3|，它的几何意义是数轴上表示数7的点与表示数3的点之间的距离．也就是说，在数轴上，如果点A表示的数记为a，点B表示的数记为b，则A，B两点间的距离就可记作|a﹣b|．
回答下列问题：
（1）几何意义是数轴上表示数2的点与数﹣3的点之间的距离的式子是 ；式子|a+5|的几何意义是 ；
（2）根据绝对值的几何意义，当|m﹣2|＝3时，m＝ ；
（3）探究：|m+1|+|m﹣9|的最小值为 ，此时m满足的条件是 ；
（4）|m+1|+|m﹣9|+|m﹣16|的最小值为 ，此时m满足的条件是 ．
22．（8分）（2021秋•江北区校级期中）已知数轴上两点A，B对应的数分别为﹣8和4，点P为数轴上一动点，若规定：点P到A的距离是点P到B的距离的3倍时，我们就称点P是关于A→B的“广益点”．
（1）若点P到点A的距离等于点P到点B的距离时，求点P表示的数是多少；
（2）若点P以每秒1个单位的速度从原点O开始向右运动，当点P是关于A→B的“广益点”时，求点P的运动时间；
（3）若点P在原点的左边（即点P对应的数为负数），且点P，A，B中，其中有一个点是关于其它任意两个点的“广益点”，请直接写出所有符合条件的点P表示的数．
23．（9分）（2022春•房山区期中）现将偶数个互不相等的有理数分成个数相同的两排，需满足第一排中的数越来越大，第二排中的数越来越小．例如，轩轩将“1，2，3，4”进行如下分组：
然后把每列两个数的差的绝对值进行相加，定义为该分组方式的“M值”．
例如，以上分组方式的“M值”为M＝|1﹣4|+|2﹣3|＝4．
（1）另写出“1，2，3，4”的一种分组方式，并计算相应的“M值”；
（2）将4个自然数“a，6，7，8”按照题目要求分为两排，使其“M值”为6，则a的值为 ．
（3）已知有理数c，d满足c+d＝2，且c＜d．将6个有理数“c，d，﹣5，﹣2，2，4”按照题目要求分为两排，使其“M值”为18，求d的值．题号
一
二
三
总分
得分
评卷人
得 分


日期
第1天
第2天
第3天
第4天
第5天
低强度
8
6
6
5
4
高强度
12
13
15
12
8
休息
0
0
0
0
0
评卷人
得 分


评卷人
得 分


星期
一
二
三
四
五
与前一天相比价格的涨跌情况/元
+0.3
﹣0.1
+0.25
+0.2
﹣0.5
当天的交易量/kg
2500
2000
3000
1500
1000

第一列
第二列
第一排
1
2
第二排
4
3
专题2.8 有理数及其运算（满分100）
学校:___________姓名：___________班级：___________考号：___________
一．选择题（本大题共10小题，每小题3分，满分30分）
1．（2022•黔东南州）下列说法中，正确的是（ ）
A．2与﹣2互为倒数B．2与12互为相反数
C．0的相反数是0D．2的绝对值是﹣2
【思路点拨】
根据倒数的定义判断A选项；根据相反数的定义判断B选项；根据0的相反数是0判断C选项；根据正数的绝对值等于它本身判断D选项．
【解题过程】
解：A选项，2与﹣2互为相反数，故该选项不符合题意；
B选项，2与12互为倒数，故该选项不符合题意；
C选项，0的相反数是0，故该选项符合题意；
D选项，2的绝对值是2，故该选项不符合题意；
故选：C．
2．（2021秋•滕州市月考）下列说法中正确的有（ ）个．①0是整数，也是正数：②﹣123是负分数；③3.2是正小数，不是正分数；④自然数一定是正数；⑤负分数一定是负有理数；⑥非负数就是正数和零．
A．0B．1C．2D．3
【思路点拨】
分别根据有理数的定义与分类以及正数和负数的定义逐一判断即可．
【解题过程】
解：①0是整数，但0既不是正数，也不是负数，故原说法错误：
②﹣123是负分数，说法正确；
③3.2是正小数，也是正分数，故原说法错误；
④自然数一定是正数，说法错误，0是自然数，但0既不是正数，也不是负数；
⑤负分数一定是负有理数，说法正确；
⑥非负数就是正数和零，说法正确．
所以说法中正确的有3个．
故选：D．
3．（2022春•东台市月考）某种细胞开始分裂时有两个，1小时后分裂成4个并死去一个，2小时后分裂成6个并死去一个，3小时后分裂成10个并死去一个，按此规律，8小时后细胞存活的个数是（ ）
A．253B．255C．257D．259
【思路点拨】
根据题意，n个小时后细胞存活的个数是2n+1，求出n＝8时的值即可．
【解题过程】
解：根据题意，1小时后分裂成4个并死去1个，剩3个，3＝2+1；
2小时后分裂成6个并死去1个，剩5个，5＝22+1；
3小时后分裂成10个并死去一个，剩9个，9＝23+1；
……
n个小时后细胞存活的个数是2n+1，
当n＝8时，存活个数是28+1＝257．
故选：C．
4．（2021秋•新华区校级期中）若a，b互为相反数，且ab≠0，c、d互为倒数，|m|＝2，则（a+b）2021+（ba）3﹣3cd+2m的值（ ）
A．0B．0或﹣8C．﹣2成6D．2或﹣6
【思路点拨】
根据相反数、倒数、绝对值得出a+b＝0，ba=−1，cd＝1，m＝±2，代入求出即可．
【解题过程】
解：∵a、b互为相反数，且ab≠0，c、d互为倒数，|m|＝2，
∴a+b＝0，ba=−1，cd＝1，m＝±2，
当m＝2时，（a+b）2021+（ba）3﹣3cd+2m＝02021+（﹣1）3﹣3×1+2×2＝0﹣1﹣3+4＝0，
当m＝﹣2时，（a+b）2021+（ba）3﹣3cd+2m＝02021+（﹣1）3﹣3×1+2×（﹣2）＝0﹣1﹣3﹣4＝﹣8．
故（a+b）2021+（ba）3﹣3cd+2m的值是0或﹣8．
故选：B．
5．（2020秋•江阴市校级月考）电子跳蚤落在数轴上的某点K0，第一步从K0向左跳1个单位到K1，第二步由K1向右跳2个单位到K2，第三步由K2向左跳3个单位到K3，第四步由K3跳4个单位到K4，…，按以上规律跳了100步时，电子跳蚤落在数轴上的点K100所表示的数恰是30，则电子跳蚤的初始位置K0点所表示的数为（ ）
A．﹣26B．﹣20C．﹣30D．30
【思路点拨】
设电子跳蚤落在数轴上的某点K0＝a，规定向左为负，向右为正，根据题意列出方程，再进一步根据有理数的加法法则进行计算．
【解题过程】
解：设电子跳蚤落在数轴上的某点K0＝a，规定向左为负，向右为正．
根据题意，得a﹣1+2﹣3+4﹣…+100＝30，
a+（2﹣1）+…+（100﹣99）＝30，
a+50＝30，
a＝﹣20．
故选：B．
6．（2022•钟山县模拟）计算：1+12+122+123+124+⋯⋯+1299+12100结果是（ ）
A．1−12100B．1−12101C．2−12100D．2−12101
【思路点拨】
根据2×（12+122+123+124+⋯⋯+1299+12100）＝1+12+122+123+124+⋯⋯+1299，可得12+122+123+124+⋯⋯+1299+12100=1+12+122+123+124+⋯⋯+1299−（12+122+123+124+⋯⋯+1299+12100）＝1−12100计算即可求解．
【解题过程】
解：1+12+122+123+124+⋯⋯+1299+12100
＝1+1−12100
＝2−12100．
故选：C．
7．（2022春•岳麓区校级月考）在一次数学活动课上，某数学老师在4张同样的纸片上各写了一个正整数，从中随机取2张，并将它们上面的数相加，重复这样做，每次所得的和都是5，6，7，8中的一个数，并且这4个数都能取到，根据以上信息，下列判断正确的是（ ）
A．四个正整数中最小的是1
B．四个正整数中最大的是8
C．四个正整数中有两个是2
D．四个正整数中一定有3
【思路点拨】
分别列出两数相加为5，6，7，8的所有可能性求解．
【解题过程】
解：相加得5的两个整数可能为：1，4或2，3．
相加得6的两个整数可能为：1，5或2，4或3，3．
相加得7的两个整数可能为：1，6或2，5或3，4．
相加得8的两个整数可能为：1，7或2，6或3，5或4，4．
∵每次所得两个整数和最小是5，
∴最小两个数字为2，3，
∵每次所得两个整数和最大是8，
∴最大数字为4或5，
当最大数字为4的时，四个整数分别为2，3，4，4．
当最大数字为5时，四个整数分别为2，3，3，5．
∴四个正整数中一定有3．
故选：D．
8．（2022•平邑县一模）小云计划户外徒步锻炼，每天有“低强度”“高强度”“休息”三种方案，下表对应了每天不同方案的徒步距离（单位：km）．若选择“高强度”要求前一天必须“休息”（第一天可选择“高强度”）．则小云5天户外徒步锻炼的最远距离为（ ）km．
A．35B．36C．37D．38
【思路点拨】
根据“高强度”要求前一天必须“休息”，则如果“高强度”的距离比前一天+当天的“低强度”距离短的话，则没有必要选择“高强度”，因此只有第一天和第三天适合选择“高强度”计算出此时的距离即可．
【解题过程】
解：∵“高强度”要求前一天必须“休息”，
∴当“高强度”的徒步距离＞前一天“低强度”距离+当天“低强度”距离时选择“高强度”能使徒步距离最远，
∵15＞6+6，12＞6+5，
∴适合选择“高强度”的是第三天和第四天，
又∵第一天可选择“高强度”，
∴方案①第一天选择“高强度”，第二天“休息”，第三天选择“高强度”，第四天和第五天选择“低强度”，
此时徒步距离为：12+0+15+5+4＝36（km），
方案②第一天选择“高强度”，第二天选择“低强度”，第三天选择“休息”，第四天选择“高强度”，第五天选择“低强度”，
此时徒步距离为：12+6+0+12+4＝34（km），
综上，徒步的最远距离为36km．
故选：B．
9．（2020秋•江夏区校级月考）观察下列等式：12＝1，22＝4，32＝9，42＝16，52＝25，…，若12+22+32+42+52+…+n2的个位数字是1（0＜n≤2020，且n为整数），则n的最大值是（ ）
A．2001B．2006C．2011D．2019
【思路点拨】
通过计算发现每10个数，末位数字循环一次，再结合选项进行判断即可求解．
【解题过程】
解：∵12＝1，22＝4，32＝9，42＝16，52＝25，62＝36，72＝49，82＝64，92＝81，102＝100，112＝121，122＝144，132＝169，…，
∴每10个数，末位数字循环一次，
∴1+4+9+6+5+6+9+1+0＝45，
∵2001÷10＝200……1，
∴200×45+1＝9001；
∵2006÷10＝200……6，
∴200×45+1+4+9+6+5+6＝9031；
∵2011÷10＝201……1，
∴201×45+1＝9046；
∵2019÷10＝201……9，
∴202×45＝9090；
∵2006＞2001，
∴n的最大值为2006，
故选：B．
10．（2021秋•江岸区校级月考）下列说法中，正确的个数是（ ）
①若|1a|=1a，则a≥0；②若|a|＞|b|，则有（a+b）（a﹣b）是正数；
③A、B、C三点在数轴上对应的数分别是﹣2、6、x，若相邻两点的距离相等，则x＝2；
④若代数式2x+|9﹣3x|+|1﹣x|+2011的值与x无关，则该代数式值为2021；
⑤a+b+c＝0，abc＜0，则b+c|a|+a+c|b|+a+b|c|的值为±1．
A．1个B．2个C．3个D．4个
【思路点拨】
根据各个小题中的说法，可以判断是否正确，尤其是对于错误的结论，我们只要说明理由或者举出反例即可．
【解题过程】
解：若|1a|=1a，则a＞0，故①错误，不合题意；
若|a|＞|b|，
则a＞b＞0或a＞0＞b＞﹣a或﹣a＞b＞0＞a或0＞a＞b，
当a＞b＞0时，则有（a+b）（a﹣b）＞0是正数，
当a＞0＞b＞﹣a时，则有（a+b）（a﹣b）＞0是正数，
当﹣a＞b＞0＞a时，则有（a+b）（a﹣b）＞0是正数，
当0＞a＞b时，则有（a+b）（a﹣b）＞0是正数，
由上可得，（a+b）（a﹣b）＞0是正数，故②正确，符合题意；
A、B、C三点在数轴上对应的数分别是﹣2、6、x，若相邻两点的距离相等，则x＝2或﹣10或14，故③错误，不合题意；
若代数式2x+|9﹣3x|+|1﹣x|+2011的值与x无关，则2x+|9﹣3x|+|1﹣x|+2011＝2x+9﹣3x+x﹣1+2011＝2019，故④错误，不合题意；
∵a+b+c＝0，abc＜0，
∴a、b、c中一定是一负两正，b+c＝﹣a，a+c＝﹣b，a+b＝﹣c，
不妨设a＞0，b＜0，c＜0，
∴b+c|a|+a+c|b|+a+b|c|
=−aa+−b−b+−c−c
＝﹣1+1+1
＝1，故⑤错误，不合题意；
故选：A．
二．填空题（本大题共5小题，每小题3分，满分15分）
11．（2021秋•东城区期末）现把2021个连续整数1，2，3…2021的每个数的前面任意填上“+”号或者“﹣”号，然后将它们相加，则所得的结果绝对值的最小值为 1 ．
【思路点拨】
根据有理数和绝对值的意义，得出绝对值和最小时数的符号规律，进而求出答案．
【解题过程】
解：根据绝对值的意义和题意可得，
∵2021÷4＝505……1，
∴1+2﹣3﹣4+5+6﹣7﹣8+9+10﹣11﹣12+13……+2018﹣2019﹣2020+2021
＝1+（2﹣3﹣4+5）+（6﹣7﹣8+9）+（10﹣11﹣12+13）+……+（2018﹣2019﹣2020+2021）
＝1+0+0+……+0
＝1，
故答案为：1．
12．（2021秋•公安县期末）小聪在纸上画了一条数轴后，折叠纸面，使数轴上表示﹣2的点与表示5的点重合，若数轴上A，B两点之间的距离为10，且A，B两点经上述折叠后重合，则B点表示的数为 6.5或﹣3.5 ．
【思路点拨】
折叠后数轴上表示﹣2的点与表示5的点重合，点﹣2和点5的中点是1.5，数轴上A，B两点经上述折叠后重合，且A，B两点之间的距离为10，则A点与B点到1.5的距离都是5，进而求出B点表示的数即可．
【解题过程】
解：折叠后数轴上表示﹣2的点与表示5的点重合，
折叠点为﹣2和5的中点：1.5．
∵数轴上A，B两点经上述折叠后重合，且A，B两点之间的距离为10，
∴A点与B点到1.5的距离都是5，
当B点在中点右侧时，对应的数为1.5+5＝6.5，
当B点在中点左侧时，对应的数是1.5﹣5＝﹣3.5．
故答案为：6.5或﹣3.5．
13．（2021秋•大田县期中）三个整数a，b，c满足a＜b＜c，且a+b+c＝0．若|a|＜10，则|a|+|b|+|c|的最大值为 34 ．
【思路点拨】
根据a+b+c＝0，a＜b＜c，可得a＜0，c＞0，a+b＜0，则|a|＞|b|，再由|a|＜10，a，b，c都是整数，得到|a|≤9，则|b|≤8，根据|a+b|＝﹣（b+a）＝﹣b﹣a，|b|≥﹣b，|a|≥a，即可得到|c|＝|﹣a﹣b|＝|a+b|≤|a|+|b|≤17，由此求解即可．
【解题过程】
解：∵a+b+c＝0，a＜b＜c，
∴a＜0，c＞0，a+b＜0，
∴|a|＞|b|，
∵|a|＜10，a，b，c都是整数，
∴|a|≤9，
∴|b|≤8，
∵|a+b|＝﹣（b+a）＝﹣b﹣a，|b|≥﹣b，|a|≥a，
∴|c|＝|﹣a﹣b|＝|a+b|≤|a|+|b|≤17，
∴|a|+|b|+|c|的值最大为9+8+17＝34，
故答案为：34．
14．（2021春•杨浦区校级期末）已知a，b，c为整数，且|a﹣b|2021+|c﹣a|2020＝1，则|a﹣b|+|b﹣c|+|c﹣a|＝ 0或2 ．
【思路点拨】
因为a、b、c都为整数，而且|a﹣b|2021+|c﹣a|2020＝1，所以|a﹣b|与|c﹣a|只能是0或者1，于是进行分类讨论即可得出．
【解题过程】
解：∵a、b、c为整数，且|a﹣b|2021+|c﹣a|2020＝1，
∴有|a﹣b|＝1，|c﹣a|＝0或|a﹣b|＝0，|c﹣a|＝1
①若|a﹣b|＝1，|c﹣a|＝0，
则a﹣b＝±1，a＝c，
∴|b﹣c|＝|c﹣b|＝|a﹣b|＝1，
∴|a﹣b|+|b﹣c|﹣|c﹣a|＝1+1+0＝2，
②|a﹣b|＝0，|c﹣a|＝1，
则a＝b，c﹣a＝±1，
∴|b﹣c|＝|c﹣b|＝|c﹣a|＝1，
∴|a﹣b|+|b﹣c|﹣|c﹣a|＝0+1﹣1＝0，
故答案为：0或2．
15．（2020秋•鄞州区期末）已知整数a，b，c，d的绝对值均小于5，且满足1000a+100b2+10c3+d4＝2021，则abcd的值为 ±4 ．
【思路点拨】
先根据条件确认个位上的1一定为d4产生，得d＝±1或±3，①当d＝±1时，d4＝1，②当d＝±3时，d4＝81，分别代入计算可得答案．
【解题过程】
解：∵1000a+100b2+10c3+d4＝2021，整数a，b，c，d的绝对值均小于5，
∴个位上的1一定为d4产生，（±3）4＝81，（±1）4＝1，
∴d＝±1或±3，
①当d＝±1时，d4＝1，
∴1000a+100b2+10c3＝2020，
∴100a+10b2+c3＝202，
∴个位上的2是由c3产生的，
∴c3＝2或﹣8（﹣4～4中没有立方的个位数是2的），
∴c3＝﹣8，
∴c＝﹣2，
∴100a+10b2﹣8＝202，
100a+10b2＝210，
10a+b2＝21，
∴个位上的1是由b2产生的，（±1）2＝1，
∴当b＝±1时，10a＝20，a＝2，
∴abcd=2×1×(−2)×1=−42×(−1)×(−2)×1=42×1×(−2)×(−1)=42×(−1)×(−2)×(−1)=−4，
∴abcd＝±4；
②当d＝±3时，d4＝81，
∴1000a+100b2+10c3＝2021﹣81＝1940，
∴100a+10b2+c3＝194，
同理43＝64，
∴c＝4，
∴100a+10b2+64＝194，
100a+10b2＝130，
10a+b2＝13，
不存在整数满足条件，
故d≠±3；
综上，abcd＝±4．
故答案为：±4．
三．解答题（本大题共8小题，满分55分）
16．（2021秋•随县期末）计算：
①﹣2×3﹣|﹣4|；
②﹣32+（−12）×（﹣8）+（﹣6）2；
③（134−78−712）×（﹣117）；
④8÷（﹣6）﹣[﹣3+116×（−27）]．
【思路点拨】
①先算乘法和去绝对值，然后计算减法即可；
②先算乘方，然后算乘法、最后算加法即可；
③根据乘法分配律计算即可；
④先算括号内的式子，然后算括号外的除法、最后算减法．
【解题过程】
解：①﹣2×3﹣|﹣4|
＝﹣6﹣4
＝﹣10；
②﹣32+（−12）×（﹣8）+（﹣6）2
＝﹣9+4+36
＝31；
③（134−78−712）×（﹣117）
=74×（−87）−78×（−87）−712×（−87）
＝﹣2+1+23
=−13；
④8÷（﹣6）﹣[﹣3+116×（−27）]
＝8÷（﹣6）﹣（﹣3−76×27）．
＝8÷（﹣6）﹣（﹣3−13）
＝8÷（﹣6）+103
=−43+103
＝2．
17．（2022春•南岸区校级月考）我国约有9600000平方千米的土地，平均1平方千米的土地一年从太阳得到的能量相当于燃烧150000吨煤所产生的能量．
（1）一年内我国土地从太阳得到的能量相当于燃烧多少吨煤所产生的能量？
（2）若1吨煤大约可以发出8000度电，那么（1）中的煤大约发出多少度电？（结果用科学记数法表示）
【思路点拨】
（1）根据乘法的意义列出算式（9.6×106）×（1.5×105）计算，再用科学记数法表示即可；
（2）用（1）的结果乘以8×103，求出结果后再用科学记数法表示即可．
【解题过程】
解：（1）（9.6×106）×（1.5×105）
＝（9.6×1.5）×（106×105）
＝1.44×1012（吨）．
答：一年内我国土地从太阳得到的能量相当于燃烧1.44×1012吨煤．
（2）（1.44×1012）×（8×103）
＝（1.44×8）×（1012×103）
＝1.152×1016（度）．
答：（1）中的煤大约发出1.152×1016度电．
18．（2021秋•邹城市期中）已知下列各有理数：a，b，c的大小关系为a＜﹣1＜b＜0＜1＜c．
（1）画出数轴，在数轴上标出这些数表示的点；
（2）在横线上填上合适的符号（＞或＜或＝）：
①a+c ＜ b+c；②a﹣c ＜ a﹣b；③ab ＞ ac；④ab ＞ ac；
（3）化简：|a+b|﹣|b﹣c|﹣|1﹣c|．
【思路点拨】
（1）准确把握a，b，c，三点在数轴上的位置即可；
（2）利用特殊值法，例如a＝﹣2，b=−12，c＝2，计算出各式的值，再进行比较；
（3）利用绝对值的意义，先化简各式，再进行计算．
【解题过程】
解：（1）在数轴上表示各数如图所示：
（2）当a＝﹣2，b=−12，c＝2时，
①∵a+c＝0，b+c=32，
∴a+c＜b+c，
②∵a﹣c＝﹣4，a﹣b=−32
∴a﹣c＜a﹣b，
③∵ab＝1，ac＝﹣4，
∴ab＞ac，
④∵ab=4，ac=−1，
∴ab＞ac，
（3）|a+b|﹣|b﹣c|﹣|1﹣c|
＝﹣（a+b）﹣（c﹣b）﹣（c﹣1）
＝﹣a﹣b﹣c+b﹣c+1
＝﹣a﹣2c+1．
19．（2022•义安区模拟）观察以下算式：
①1×11×5=18×(1+31×5)；
②2×35×9=18×(1+35×9)；
③3×59×13=18×(1+39×13)．
（1）请写出第④个算式： 4×713×17=18×(1+313×17) ．
（2）请用n（n是正整数）表示出第n个算式，并计算1×11×5+2×35×9+3×59×13+⋯+9×1733×37+10×1937×41．
【思路点拨】
（1）观察已知等式即可写出第④个式子；
（2）结合（1）即可用n（n是正整数）表示出第n个算式，再根据发现的规律解决问题即可．
【解题过程】
解：（1）∵①1×11×5=18×(1+31×5)；
②2×35×9=18×(1+35×9)；
③3×59×13=18×(1+39×13)．
∴第④个算式：4×713×17=18×(1+313×17)．
故答案为：4×713×17=18×(1+313×17)；
（2）第n个算式：n(2n−1)(4n−3)(4n+1)=18×(1+3(4n−3)(4n+1))；
1×11×5+2×35×9+3×59×13+⋯+9×1733×37+10×1937×41
=18×（1+31×5）+18×（1+35×9）+•••+18×（1+333×37）+18×（1+337×41）
=18×（10+31×5+35×9+•••+333×37+337×41）
=18×10+18×34×（1−15+15−19+•••+133−137+137−141）
=54+18×34×4041
=5541．
20．（2021秋•汝阳县期末）某批发商于上周日买进某产品10000kg，每千克2.4元，进入批发市场后共占5个摊位，每个摊位最多能容纳2000kg该品种的产品，每个摊位的市场管理价为每天20元．如表为本周内该产品每天的批发价格比前一天的涨跌情况．（涨记为正，跌记为负，上周日当天的售价刚好为每千克2.4元）
（1）星期四该产品价格为每千克多少元？
（2）本周内该产品的最高价格为每千克多少元？最低价格为每千克多少元？
（3）该批发商在销售过程中采用逐步减少摊位个数（每天减少一个）的方法来降低成本，增加收益，请你帮他算一算，这样他在本周的买卖中共赚了多少钱？
【思路点拨】
（1）根据价格的涨跌情况即可作出判断；
（2）计算出每天的价格即可作出判断；
（3）根据售价﹣进价﹣摊位费用＝收益，即可进行计算．
【解题过程】
解：（1）2.4+0.3﹣0.1+0.25+0.2＝3.05（元）；
答：星期四该产品价格为每千克3.05元；
（2）星期一的价格是：2.4+0.3＝2.7（元）；
星期二的价格是：2.7﹣0.1＝2.6（元）；
星期三的价格是：2.6+0.25＝2.85（元）；
星期四是：2.85+0.2＝3.05（元）；
星期五是：3.05﹣0.5＝2.55（元）；
因而本周内该农产品的最高价格为每斤3.05元，最低价格为每斤2.55元；
（3）（2500×2.7﹣5×20）+（2000×2.6﹣4×20）+（3000×2.85﹣3×20）+（1500×3.05﹣2×20）+（1000×2.55﹣20）﹣10000×2.4
＝6650+5120+8490+4535+2530﹣24000
＝27325﹣24000
＝3325（元）．
答：他在本周的买卖中共赚了3325元钱．
21．（2021秋•嘉鱼县期末）数轴是一个非常重要的数学工具，它使数和数轴上的点建立起一一对应的关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．我们知道|4|＝|4﹣0|，它的几何意义是数轴上表示4的点与原点（即表示0的点）之间的距离，又如式子|7﹣3|，它的几何意义是数轴上表示数7的点与表示数3的点之间的距离．也就是说，在数轴上，如果点A表示的数记为a，点B表示的数记为b，则A，B两点间的距离就可记作|a﹣b|．
回答下列问题：
（1）几何意义是数轴上表示数2的点与数﹣3的点之间的距离的式子是 |2﹣（﹣3）| ；式子|a+5|的几何意义是 数轴上表示数a的点与数﹣5的点之间的距离 ；
（2）根据绝对值的几何意义，当|m﹣2|＝3时，m＝ ﹣1或5 ；
（3）探究：|m+1|+|m﹣9|的最小值为 10 ，此时m满足的条件是 ﹣1≤m≤9 ；
（4）|m+1|+|m﹣9|+|m﹣16|的最小值为 17 ，此时m满足的条件是 m＝9 ．
【思路点拨】
（1）根据两点间的距离公式即可求解；
（2）根据||a﹣b|的几何意义求解可得；
（3）根据m＜﹣1，﹣1≤m≤9，m＞9三种情况确定最小值和此时m的取值；
（4）|m+1|+|m﹣9|+|m﹣16|＝（|m+1|+|m﹣16|）+|m﹣9|，根据问题（3）可知，要使|m+1|+|m﹣16|的值最小，m的值只要取﹣1到16之间（包括﹣1、16）的任意一个数，要使|m﹣9|的值最小，m应取9，显然当m＝9时能同时满足要求，从而得结论．
【解题过程】
解：（1）数轴上表示数2的点与数﹣3的点之间的距离的式子是|2﹣（﹣3）|；
式子|a+5|的几何意义是数轴上表示数a的点与数﹣5的点之间的距离；
故答案为：|2﹣（﹣3）|，数轴上表示数a的点与数﹣5的点之间的距离；
（2）等式|m﹣2|＝3的几何意义是表示m到数2的距离为3的点，
则m的值为﹣1或5；
故答案为：﹣1或5；
（3）式子|m+1|+|m﹣9|表示数m到﹣1和9的距离之和，
当m＜﹣1时，原式＝﹣m﹣1﹣m+9＝﹣2m+8＞10，
当﹣1≤m≤9时，原式＝m+1+9﹣m＝10，
当m＞9时，原式＝m+1+m﹣9＝2m﹣8＞10，
故式子|m+1|+|m﹣9|的最小值为10，此时m满足的条件是﹣1≤m≤9；
（4）由分析可知，
|m+1|+|m﹣9|+|m﹣16|的最小值为17，此时m满足的条件是m＝9．
22．（2021秋•江北区校级期中）已知数轴上两点A，B对应的数分别为﹣8和4，点P为数轴上一动点，若规定：点P到A的距离是点P到B的距离的3倍时，我们就称点P是关于A→B的“广益点”．
（1）若点P到点A的距离等于点P到点B的距离时，求点P表示的数是多少；
（2）若点P以每秒1个单位的速度从原点O开始向右运动，当点P是关于A→B的“广益点”时，求点P的运动时间；
（3）若点P在原点的左边（即点P对应的数为负数），且点P，A，B中，其中有一个点是关于其它任意两个点的“广益点”，请直接写出所有符合条件的点P表示的数．
【思路点拨】
（1）根据点P到点A的距离等于点P到点B的距离即可得到结论；
（2）根据题意可得PA＝t+8，PB＝|4﹣t|，再根据“广益点”的定义即可求解；
（3）分五种情况进行讨论：当点A是关于P→B的“广益点”时；当点A是关于B→P的“广益点”时；当点P是关于A→B的“广益点”时；当点P是关于B→A的“广益点”时；当点B是关于P→A的“广益点”时，分别代入计算即可．
【解题过程】
解：（1）∵数轴上两点A，B对应的数分别为﹣8和4，
∴AB＝4﹣（﹣8）＝12，
∵点P到点A的距离等于点P到点B的距离，
∴点P是AB的中点，
∴BP＝AP=12AB＝6，
∴点P表示的数为﹣2；
（2）设点P运动时间为t秒，
根据题意可知，PA＝t+8，PB＝|4﹣t|，
∴t+8＝3|4﹣t|，
解得：t＝1或10，
∴点P运动的时间为1秒或10秒；
（3）设点P表示的数为n，
根据题意可得，PA＝n+8或﹣n﹣8，PB＝4﹣n，AB＝12，
分五种情况进行讨论：
①当点A是关于P→B的“广益点”时，
得PA＝3AB，
即﹣n﹣8＝36，解得n＝﹣44；
②当点A是关于B→P的“广益点”时，
得AB＝3AP，
即3（﹣n﹣8）＝12，解得n＝﹣12；
或3（n+8）＝12，解得n＝﹣4；
③当点P是关于A→B的“广益点”时，
得PA＝3PB，
即﹣n﹣8＝3（4﹣n），解得n＝10；（不符合题意，舍去）
或n+8＝3（4﹣n），解得n＝1（不符合题意，舍去）；
④当点P是关于B→A的“广益点”时，
得PB＝3AB，
即4﹣n＝3（n+8），解得n＝﹣5；
或4﹣n＝3（﹣n﹣8），解得n＝﹣14；
⑤当点B是关于P→A的“广益点”时，
得BP＝3AB，
即4﹣n＝36，解得n＝﹣32，
综上所述，所有符合条件的点P表示的数是：﹣4，﹣5，﹣12，﹣14，﹣32，﹣44．
23．（2022春•房山区期中）现将偶数个互不相等的有理数分成个数相同的两排，需满足第一排中的数越来越大，第二排中的数越来越小．例如，轩轩将“1，2，3，4”进行如下分组：
然后把每列两个数的差的绝对值进行相加，定义为该分组方式的“M值”．
例如，以上分组方式的“M值”为M＝|1﹣4|+|2﹣3|＝4．
（1）另写出“1，2，3，4”的一种分组方式，并计算相应的“M值”；
（2）将4个自然数“a，6，7，8”按照题目要求分为两排，使其“M值”为6，则a的值为 3或11 ．
（3）已知有理数c，d满足c+d＝2，且c＜d．将6个有理数“c，d，﹣5，﹣2，2，4”按照题目要求分为两排，使其“M值”为18，求d的值．
【思路点拨】
（1）按要求分组，利用分组方式的“M值”的意义计算即可；
（2）利用分类讨论的方法，分0＜a＜6和a＞8两种情况解答，按要求分组，利用分组方式的“M值”的意义计算即可；
（3）利用分类讨论的方法，分c＜﹣5，﹣5＜c＜﹣2，﹣2＜c＜1，1＜d＜2四种情况解答，按要求分组，利用分组方式的“M值”的意义计算即可．
【解题过程】
解：（1）将“1，2，3，4”进行如下分组：
∴以上分组方式的“M值”为：M＝|1﹣4|+|3﹣2|＝4；
（2）①当0＜a＜6时，
将4个自然数“a，6，7，8”按照题目要求进行如下分组：
∵以上分组方式的“M值”为6，
∴|a﹣8|+|7﹣6|＝6．
∴a＝3；
②当a＜8时，
将4个自然数“a，6，7，8”按照题目要求进行如下分组：
∵以上分组方式的“M值”为6，
∴|a﹣6|+|7﹣8|＝6．
∴a＝11；
综上，a＝3或11．
故答案为：3或11；
（3）∵c+d＝2，且c＜d，
∴c＝2﹣d，c＜1，d＞1．
①当c＜﹣5时，则d＞7，
将6个有理数“c，d，﹣5，﹣2，2，4”按照题目要求进行如下分组：
∵以上分组方式的“M值”为18，
∴|2﹣d﹣d|+|﹣5﹣4|+|﹣2﹣2|＝18．
解得：d=72（不合题意，舍去）．
②当﹣5＜c＜﹣2时，则4＜d＜7，
将6个有理数“c，d，﹣5，﹣2，2，4”按照题目要求进行如下分组：
∵以上分组方式的“M值”为18，
∴|﹣5﹣d|+|2﹣d﹣4|+|﹣2﹣2|＝18．
∴d=72（不合题意，舍去）．
③当﹣2＜c＜1时，则1＜d＜4，
将6个有理数“c，d，﹣5，﹣2，2，4”按照题目要求进行如下分组：
∵以上分组方式的“M值”为18，
∴|﹣5﹣4|+|﹣2﹣d|+|2﹣d﹣2|＝18．
∴d=72（符合题意）．
④当1＜d＜2时，
∵以上分组方式的“M值”为18，
∴|﹣5﹣4|+|﹣2﹣2|+|2﹣d﹣d|＝18．
∴d=72（不合题意，舍去）．
综上分析可得：d=72．题号
一
二
三
总分
得分
评卷人
得 分


日期
第1天
第2天
第3天
第4天
第5天
低强度
8
6
6
5
4
高强度
12
13
15
12
8
休息
0
0
0
0
0
评卷人
得 分


评卷人
得 分


星期
一
二
三
四
五
与前一天相比价格的涨跌情况/元
+0.3
﹣0.1
+0.25
+0.2
﹣0.5
当天的交易量/kg
2500
2000
3000
1500
1000

第一列
第二列
第一排
1
2
第二排
4
3