

所属成套资源:中考数学二轮复习核心考点专题提优拓展训练(原卷版+解析)
- 中考数学二轮复习核心考点专题提优拓展训练专题04一元二次方程根的判别式的应用及根与系数的关系的应用(原卷版+解析) 试卷 0 次下载
- 中考数学二轮复习核心考点专题提优拓展训练专题05函数图像信息题(原卷版+解析) 试卷 0 次下载
- 中考数学二轮复习核心考点专题提优拓展训练专题09二次函数抛物线与三角形存在性问题(原卷版+解析) 试卷 0 次下载
- 中考数学二轮复习核心考点专题提优拓展训练专题10二次函数与平行四边形含矩形菱形正方形的存在性问题(原卷版+解析) 试卷 0 次下载
- 中考数学二轮复习核心考点专题提优拓展训练专题11反比例函数与一次函数二次函数的综合运用(原卷版+解析) 试卷 0 次下载
中考数学二轮复习核心考点专题提优拓展训练专题08一次函数与反比例函数的实际应用(原卷版+解析)
展开这是一份中考数学二轮复习核心考点专题提优拓展训练专题08一次函数与反比例函数的实际应用(原卷版+解析),共24页。试卷主要包含了一次函数的实际应用,反比例函数的实际应用,一次函数与反比例函数的综合运用等内容,欢迎下载使用。
(1)方案选择问题
1. (2023•内蒙古)某商店决定购进A、B两种北京冬奥会纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品的单价;
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且购进B种纪念品数量不少于20件,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?求出最大利润.
2. (2023•东莞市校级二模)某移动通讯公司推出两种移动电话计费方式:
方式一:月租费60元,主叫150分钟内不再收费,超过限定时间的部分a元/分钟;被叫免费.
方式二:月租费100元,主叫380分钟内不再收费,超过限定时间的部分0.25元/分钟;被叫免费.
两种方式的月计费y(单位:元)关于主叫时间t(单位:分钟)的函数图象如图.
(1)求a的值;
(2)结合题意和函数图象,分别求出函数图象中,射线BC和射线EF对应的月计费y(单位:元)关于主叫时间t(单位:分钟)的函数关系式,并写出对应的t的取值范围;
(3)通过计算,写出当月主叫通话时间y(单位:分钟)满足什么条件时,选择方式一省钱.
最大利润问题
3. (2023•襄阳)为了振兴乡村经济,我市某镇鼓励广大农户种植山药,并精加工成甲、乙两种产品、某经销商购进甲、乙两种产品,甲种产品进价为8元/kg;乙种产品的进货总金额y(单位:元)与乙种产品进货量x(单位:kg)之间的关系如图所示.已知甲、乙两种产品的售价分别为12元/kg和18元/kg.
(1)求出0≤x≤2000和x>2000时,y与x之间的函数关系式;
(2)若该经销商购进甲、乙两种产品共6000kg,并能全部售出.其中乙种产品的进货量不低于1600kg,且不高于4000kg,设销售完甲、乙两种产品所获总利润为w元(利润=销售额﹣成本),请求出w(单位:元)与乙种产品进货量x(单位:kg)之间的函数关系式,并为该经销商设计出获得最大利润的进货方案;
(3)为回馈广大客户,该经销商决定对两种产品进行让利销售.在(2)中获得最大利润的进货方案下,甲、乙两种产品售价分别降低a元/kg和2a元/kg,全部售出后所获总利润不低于15000元,求a的最大值.
4.某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过10.57万元购进40台电脑,其中A型电脑每台进价2500元,B型电脑每台进价2800元,A型每台售价3000元,B型每台售价3200元,预计销售额不低于12.32万元.设A型电脑购进x台、商场的总利润为y(元).
(1)请你设计出进货方案;
(2)求出总利润y(元)与购进A型电脑x(台)的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
(3)行程问题
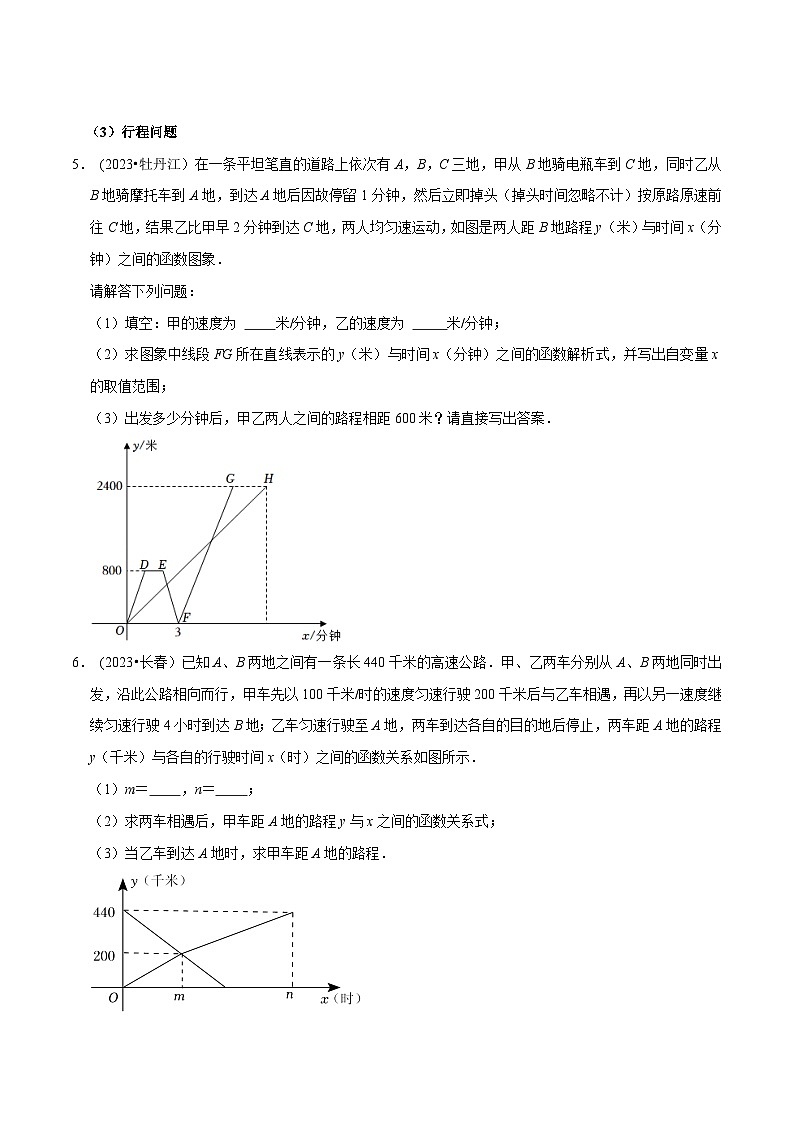
5. (2023•牡丹江)在一条平坦笔直的道路上依次有A,B,C三地,甲从B地骑电瓶车到C地,同时乙从B地骑摩托车到A地,到达A地后因故停留1分钟,然后立即掉头(掉头时间忽略不计)按原路原速前往C地,结果乙比甲早2分钟到达C地,两人均匀速运动,如图是两人距B地路程y(米)与时间x(分钟)之间的函数图象.
请解答下列问题:
(1)填空:甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)求图象中线段FG所在直线表示的y(米)与时间x(分钟)之间的函数解析式,并写出自变量x的取值范围;
(3)出发多少分钟后,甲乙两人之间的路程相距600米?请直接写出答案.
6. (2023•长春)已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止,两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.
(1)m= ,n= ;
(2)求两车相遇后,甲车距A地的路程y与x之间的函数关系式;
(3)当乙车到达A地时,求甲车距A地的路程.
类型二 反比例函数的实际应用
7. (2023•广州)某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2)与其深度d(单位:m)是反比例函数关系,它的图象如图所示.
(1)求储存室的容积V的值;
(2)受地形条件限制,储存室的深度d需要满足16≤d≤25,求储存室的底面积S的取值范围.
8. (2023•台州)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数解析式.
(2)若火焰的像高为3cm,求小孔到蜡烛的距离.
类型三 一次函数与反比例函数的综合运用
9. (2023•卧龙区模拟)通过心理专家实验研究发现:初中生在数学课上听课注意力指标指标)随上课时间的变化而变化,指标达到36为认真听讲,学生注意力指标y随时间x(分钟)变化的函数图象如图所示.当0≤x<10和10≤x<20时,图象是线段,当20≤x≤45时是反比例函数的一部分.
(1)求点A对应的指标值.
(2)李老师在一节课上讲一道数学综合题需17分钟,他能否经过适当安排.使学生在认真听讲时,进行讲解,请说明理由.
10. (2023秋•东平县校级月考)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温y(℃)与时间x(min)的关系如图所示:
(1)分别写出水温上升和下降阶段y与x之间的函数关系式并注明自变量的取值范围;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待 min?
专题提优训练
1. (2023•淮安)当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是( )
A.B.
C.D.
2. (2023•宜昌)某气球内充满了一定质量m的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=mV,能够反映两个变量p和V函数关系的图象是( )
A. B. C. D.
4. (2023•鄂州一模)已知A、B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)a= ,b= .
(2)求甲、乙两车相遇后y与x之间的函数关系式.
(3)当甲车到达距B地90千米处时,求甲、乙两车之间的路程.
4. (2023春•孝感期末)民生超市计划购进甲、乙两种商品共90件进行销售,有关信息如表,
设乙种商品有x(件),销售完两种商品的总销售额为y(元).
(1)求y与x的函数关系式;
(2)若购进乙种商品不超过45件,且该超市购进这两种商品的总进货费用不超过5000元.
①问共有多少种购进方案?
②直接写出总利润的最大值(总利润=总销售额﹣总进货费用).
商品
甲
乙
进价(元/件)
60
50
售价(元/件)
100
100(其中一次性销售超过20件时,超出部分每件再让利20元)
专题08 一次函数与反比例函数的实际应用(解析版)
类型一 一次函数的实际应用
(1)方案选择问题
1. (2023•内蒙古)某商店决定购进A、B两种北京冬奥会纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品的单价;
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且购进B种纪念品数量不少于20件,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?求出最大利润.
思路引领:(1)设某商店购进A种纪念品每件需a元,购进B种纪念品每件需b元,根据条件建立二元一次方程组求出其解即可;
(2)设某商店购进A种纪念品x个,购进B种纪念品y个,根据条件的数量关系建立不等式组求出其解即可;
(3)设总利润为W元,根据总利润=两种商品的利润之和列出函数解析式,再根据函数的性质求值即可.
解:(1)设该商店购进A种纪念品每件需a元,购进B种纪念品每件需b元,
由题意,得10a+5b=10005a+3b=550,
解得a=50b=100,
∴该商店购进A种纪念品每件需50元,购进B种纪念品每件需100元;
(2)设该商店购进A种纪念品x个,购进B种纪念品y个,
根据题意,得50x+100y=10000,
由50x+100y=10000得x=200﹣2y,
把x=200﹣2y代入x≥6y,解得y≤25,
∵y≥20,
∴20≤y≤25且为正整数,
∴y可取得的正整数值是20,21,22,23,24,25,
与y相对应的x可取得的正整数值是160,158,156,154,152,150,
∴共有6种进货方案;
(3)设总利润为W元,
则W=20x+30y=﹣10y+4000,
∵﹣10<0,
∴W随y的增大而减小,
∴当y=20时,W有最大值,W最大=﹣10×20+4000=3800(元),
∴当购进A种纪念品160件,B种纪念品20件时,可获得最大利润,最大利润是3800元.
总结提升:本题考查了一次函数、一元一次不等式解实际问题的运用,解答时求出A,B两种纪念品的单价是关键.
2. (2023•东莞市校级二模)某移动通讯公司推出两种移动电话计费方式:
方式一:月租费60元,主叫150分钟内不再收费,超过限定时间的部分a元/分钟;被叫免费.
方式二:月租费100元,主叫380分钟内不再收费,超过限定时间的部分0.25元/分钟;被叫免费.
两种方式的月计费y(单位:元)关于主叫时间t(单位:分钟)的函数图象如图.
(1)求a的值;
(2)结合题意和函数图象,分别求出函数图象中,射线BC和射线EF对应的月计费y(单位:元)关于主叫时间t(单位:分钟)的函数关系式,并写出对应的t的取值范围;
(3)通过计算,写出当月主叫通话时间y(单位:分钟)满足什么条件时,选择方式一省钱.
思路引领:(1)利用待定系数法可求出BC的解析式,再根据“方式一”的计费方式,也可求得BC的解析式,比较系数即可.
(2)根据两种计费方式可求出射线BC和射线EF对应的月计费y(单位:元)关于主叫时间t(单位:分钟)的函数关系式.
(3)根据(2)所求即可得出结论.
解:(1)由题图可知,M(350,100),
设BC所在直线为y=kt+b,
把B(150,60),M(350,100)代入,
得:150k+b=60350k+b=100,
解得:k=15b=30.
∴y=15t+30(t≥150).
当t>150时,y=a(t﹣150)+60=at+60﹣150a,
∴a=0.2.
(2)由(1)可知射线BC对应的月计费y关于主叫时间t的关系式为,
y1=0.2t+30,t≥150min,
又∵方式二中超过限定时间的部分0.25元/分钟,
∴y2=0.25(t﹣380)+100=0.25t+5.
∴射线EF对应的月计费y关于主叫时间t的关系式为,
y2=0.25t+5,t≥380min.
(3)①0≤t≤150min时,y1=60<y2=100;
②150≤t≤350min时,y1=0.2t+30<y2=100;
③t≥500min时,y1=0.2t+30<y2=0.25t+5.
综上所述,通话时间0≤t≤350min或t≥500min时,方式一省钱.
总结提升:考查了一元一次不等式的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.
最大利润问题
3. (2023•襄阳)为了振兴乡村经济,我市某镇鼓励广大农户种植山药,并精加工成甲、乙两种产品、某经销商购进甲、乙两种产品,甲种产品进价为8元/kg;乙种产品的进货总金额y(单位:元)与乙种产品进货量x(单位:kg)之间的关系如图所示.已知甲、乙两种产品的售价分别为12元/kg和18元/kg.
(1)求出0≤x≤2000和x>2000时,y与x之间的函数关系式;
(2)若该经销商购进甲、乙两种产品共6000kg,并能全部售出.其中乙种产品的进货量不低于1600kg,且不高于4000kg,设销售完甲、乙两种产品所获总利润为w元(利润=销售额﹣成本),请求出w(单位:元)与乙种产品进货量x(单位:kg)之间的函数关系式,并为该经销商设计出获得最大利润的进货方案;
(3)为回馈广大客户,该经销商决定对两种产品进行让利销售.在(2)中获得最大利润的进货方案下,甲、乙两种产品售价分别降低a元/kg和2a元/kg,全部售出后所获总利润不低于15000元,求a的最大值.
思路引领:(1)分当0≤x≤2000时,当x>2000时,利用待定系数法求解即可;
(2)根据题意可知,分当1600≤x≤2000时,当2000<x≤4000时,分别列出w与x的函数关系式,根据一次函数的性质可得出结论;
(3)根据题意可知,降价后,w与x的关系式,并根据利润不低于15000,可得出a的取值范围.
解:(1)当0≤x≤2000时,设y=k′x,根据题意可得,2000k′=30000,
解得k′=15,
∴y=15x;
当x>2000时,设y=kx+b,
根据题意可得,2000k+b=300004000k+b=56000,
解得k=13b=4000,
∴y=13x+4000.
∴y=15x(0≤x≤2000)13x+4000(x>2000).
(2)根据题意可知,购进甲种产品(6000﹣x)千克,
∵1600≤x≤4000,
当1600≤x≤2000时,w=(12﹣8)×(6000﹣x)+(18﹣15)•x=﹣x+24000,
∵﹣1<0,
∴当x=1600时,w的最大值为﹣1×1600+24000=22400(元);
当2000<x≤4000时,w=(12﹣8)×(6000﹣x)+18x﹣(13x+4000)=x+20000,
∵1>0,
∴当x=4000时,w的最大值为4000+20000=24000(元),
综上,w=−x+24000(1600≤x≤2000)x+20000(2000<x≤4000);
当购进甲产品2000千克,乙产品4000千克时,利润最大为24000元.
(3)根据题意可知,降价后,w=(12﹣8﹣a)×(6000﹣x)+(18﹣2a)x﹣(13x+4000)=(1﹣a)x+20000﹣6000a,
当x=4000时,w取得最大值,
∴(1﹣a)×4000+20000﹣6000a≥15000,解得a≤0.9.
∴a的最大值为0.9.
总结提升:本题考查了一次函数的应用,解题的关键是找准等量关系,正确列出函数关系式.
4.某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过10.57万元购进40台电脑,其中A型电脑每台进价2500元,B型电脑每台进价2800元,A型每台售价3000元,B型每台售价3200元,预计销售额不低于12.32万元.设A型电脑购进x台、商场的总利润为y(元).
(1)请你设计出进货方案;
(2)求出总利润y(元)与购进A型电脑x(台)的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
思路引领:(1)设A型电脑购进x台,则B型电脑购进(40﹣x)台,根据总进价不超过105700元和销售额不低于123200元建立不等式组,求出其解即可;
(2)根据利润等于售价﹣进价的数量关系分别表示出购买A型电脑的利润和B型电脑的利润就求其和就可以得出结论.
解:(1)设A型电脑购进x台,则B型电脑购进(40﹣x)台,由题意,得
2500x+2800(40−x)≤1057003000x+3200(40−x)≥123200,
解得:21≤x≤24,
∵x为整数,
∴x=21,22,23,24
∴有4种购买方案:
方案1:购A型电脑21台,B型电脑19台;
方案2:购A型电脑22台,B型电脑18台;
方案3:购A型电脑23台,B型电脑17台;
方案4:购A型电脑24台,B型电脑16台;
(2)由题意,得
y=(3000﹣2500)x+(3200﹣2800)(40﹣x),
=500x+16000﹣400x,
=100x+16000.
∵k=100>0,
∴y随x的增大而增大,
∴x=24时,y最大=18400元.
答:采用方案4,即购A型电脑24台,B型电脑16台的利润最大,最大利润是18400元.
总结提升:此题考查一次函数的应用以及一元一次不等式组的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.
(3)行程问题
5. (2023•牡丹江)在一条平坦笔直的道路上依次有A,B,C三地,甲从B地骑电瓶车到C地,同时乙从B地骑摩托车到A地,到达A地后因故停留1分钟,然后立即掉头(掉头时间忽略不计)按原路原速前往C地,结果乙比甲早2分钟到达C地,两人均匀速运动,如图是两人距B地路程y(米)与时间x(分钟)之间的函数图象.
请解答下列问题:
(1)填空:甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)求图象中线段FG所在直线表示的y(米)与时间x(分钟)之间的函数解析式,并写出自变量x的取值范围;
(3)出发多少分钟后,甲乙两人之间的路程相距600米?请直接写出答案.
思路引领:(1)利用速度=路程÷时间,找准甲乙的路程和时间即可得出结论;
(2)根据(1)中的计算可得出点G的坐标,设直线FG的解析式为:y=kx+b,将F,G的坐标代入,求解方程组即可;
(3)根据题意可知存在三种情况,然后分别计算即可.
解:(1)根据题意可知D(1,800),E(2,800),
∴乙的速度为:800÷1=800(米/分钟),
∴乙从B地到C地用时:2400÷800=3(分钟),
∴G(6,2400).
∴H(8,2400).
∴甲的速度为2400÷8=300(米/分钟),
故答案为:300;800;
(2)设直线FG的解析式为:y=kx+b(k≠0),且由图象可知F(3,0),
由(1)知G(6,2400).
∴3k+b=06k+b=2400,
解得,k=800b=−2400.
∴直线FG的解析式为:y=800x﹣2400(3≤x≤6).
(3)由题意可知,AB相距800米,BC相距2400米.
∵O(0,0),H(8,2400),
∴直线OH的解析式为:y=300x,
∵D(1,800),
∴直线OD的解析式为:y=800x,
当0≤x≤1时,甲从B地骑电瓶车到C地,同时乙从B地骑摩托车到A地,即甲乙朝相反方向走,
∴令800x+300x=600,解得x=611.
∵当2≤x≤3时,甲从B继续往C地走,乙从A地往B地走,
∴300x+800﹣800(x﹣2)=600解得x=185(不合题意,舍去)
∵当x>3时,甲从B继续往C地走,乙从B地往C地走,
∴300x+800﹣800(x﹣2)=600或800(x﹣2)﹣(300x+800)=600,
解得x=185或x=6.
综上,出发611分钟或185分钟或6分钟后,甲乙两人之间的路程相距600米.
总结提升:本题考查一次函数的应用、路程=速度×时间的关系等知识,解题的关键是读懂图象信息,将图象中的信息转化为实际行程问题,属于中考常考题型.
6. (2023•长春)已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止,两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.
(1)m= ,n= ;
(2)求两车相遇后,甲车距A地的路程y与x之间的函数关系式;
(3)当乙车到达A地时,求甲车距A地的路程.
思路引领:(1)由甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇可求出m=2,根据以另一速度继续匀速行驶4小时到达B地知n=6;
(2)用待定系数法可得y=60x+80,(2≤x≤6);
(3)求出乙的速度,即可得乙到A地所用时间,即可求得甲车距A地的路程为300千米.
解:(1)由题意知:m=200÷100=2,
n=m+4=2+4=6,
故答案为:2,6;
(2)设y=kx+b,将(2,200),(6,440)代入得:
2k+b=2006k+b=440,
解得k=60b=80,
∴y=60x+80,(2≤x≤6);
(3)乙车的速度为(440﹣200)÷2=120(千米/小时),
∴乙车到达A地所需时间为440÷120=113(小时),
当x=113时,y=60×113+80=300,
∴甲车距A地的路程为300千米.
总结提升:本题考查一次函数的应用,解题的关键是读懂题意,能正确识图.
类型二 反比例函数的实际应用
7. (2023•广州)某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2)与其深度d(单位:m)是反比例函数关系,它的图象如图所示.
(1)求储存室的容积V的值;
(2)受地形条件限制,储存室的深度d需要满足16≤d≤25,求储存室的底面积S的取值范围.
思路引领:(1)设底面积S与深度d的反比例函数解析式为S=Vd,把点(20,500)代入解析式求出V的值;
(2)由d的范围和图像的性质求出S的范围.
解:(1)设底面积S与深度d的反比例函数解析式为S=Vd,把点(20,500)代入解析式得500=V20,
∴V=10000.
(2)由(1)得S=10000d,
∵S随d的增大而减小,
∴当16≤d≤25时,400≤S≤625,
总结提升:此题主要考查反比例函数的性质和概念,解答此题的关键是找出变量之间的函数关系,难易程度适中.
8. (2023•台州)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数解析式.
(2)若火焰的像高为3cm,求小孔到蜡烛的距离.
思路引领:(1)根据待定法得出反比例函数的解析式即可;
(2)根据解析式代入数值解答即可.
解:(1)由题意设:y=kx,
把x=6,y=2代入,得k=6×2=12,
∴y关于x的函数解析式为:y=12x;
(2)把y=3代入y=12x,得,x=4,
∴小孔到蜡烛的距离为4cm.
总结提升:此题考查反比例函数的应用,关键是根据待定系数法得出反比例函数的解析式解答.
类型三 一次函数与反比例函数的综合运用
9. (2023•卧龙区模拟)通过心理专家实验研究发现:初中生在数学课上听课注意力指标指标)随上课时间的变化而变化,指标达到36为认真听讲,学生注意力指标y随时间x(分钟)变化的函数图象如图所示.当0≤x<10和10≤x<20时,图象是线段,当20≤x≤45时是反比例函数的一部分.
(1)求点A对应的指标值.
(2)李老师在一节课上讲一道数学综合题需17分钟,他能否经过适当安排.使学生在认真听讲时,进行讲解,请说明理由.
思路引领:(1)设反比例函数的解析式为y=kx,由C(20,45)求出k,可得D坐标,从而求出A的指标值;
(2)求出AB解析式,得到y≥36时,x≥325,由反比例函数y=900x可得y≥36时,x≤25,根据25−325=935>17,即可得到答案.
解:(1)设当20≤x≤45时,反比例函数的解析式为y=kx,将C(20,45)代入得:
45=k20,
解得k=900,
∴反比例函数的解析式为y=900x,
当x=45时,y=20,
∴D(45,20),
∴A(0,20),
即A对应的指标值为20;
(2)设当0≤x<10时,AB的解析式为y=mx+n,将A(0,20)、B(10,45)代入得:
20=n45=10m+n,
解得m=52n=20,
∴AB的解析式为y=52x+20,
当y≥36时,52x+20≥36,解得x≥325,
由(1)得反比例函数的解析式为y=900x,
当y≥36时,900x≥36,解得x≤25,
∴325≤x≤25时,注意力指标都不低于36,
∵指标达到36为认真听讲,
而25−325=935>17,
∴李老师能经过适当的安排,使学生在认真听讲时,进行讲解.
总结提升:本题考查函数图象的应用,涉及一次函数、反比例函数及不等式等知识,解题的关键是求出0≤x<10和20≤x≤45时的解析式.
10. (2023秋•东平县校级月考)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温y(℃)与时间x(min)的关系如图所示:
(1)分别写出水温上升和下降阶段y与x之间的函数关系式并注明自变量的取值范围;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待 min?
思路引领:(1)根据题意和函数图象可以求得a的值;根据函数图象和题意可以求得y关于x的函数关系式,注意函数图象是循环出现的;
(2)根据(1)中的函数解析式可以解答本题.
解:(1)观察图象,可知:当x=7(min)时,水温y=100(℃),
当0≤x≤7时,设y关于x的函数关系式为:y=kx+b,
b=307k+b=100,
解得k=10b=30,
即当0≤x≤7时,y关于x的函数关系式为y=10x+30,
当x>7时,设y=ax,
100=a7,得a=700,
即当x>7时,y关于x的函数关系式为y=700x,
当y=30时,x=703,
∴y与x的函数关系式为:y=10x+30(0≤x≤7)700x(7<x≤703),y与x的函数关系式每703分钟重复出现一次;
(2)将y=50代入y=10x+30,得x=2,
将y=50代入y=700x,得x=14,
∵14﹣2=12,703−12=343,
∴怡萱同学想喝高于50℃的水,她最多需要等待343min,
故答案为:343.
总结提升:本题考查反比例函数的应用、一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想和函数的思想解答.
专题提优训练
1. (2023•淮安)当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是( )
A.B.
C.D.
思路引领:根据题意得到xy=矩形面积(定值),故y与x之间的函数图象为反比例函数,且根据x、y实际意义x、y应>0,其图象在第一象限;于是得到结论.
解:∵根据题意xy=矩形面积(定值),
∴y是x的反比例函数,(x>0,y>0).
故选:B.
总结提升:本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
2. (2023•宜昌)某气球内充满了一定质量m的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=mV,能够反映两个变量p和V函数关系的图象是( )
A.B.
C.D.
思路引领:直接利用反比例函数的性质,结合p,V的取值范围得出其函数图象分布在第一象限,即可得出答案.
解:∵气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=mV(V,p都大于零),
∴能够反映两个变量p和V函数关系的图象是:.
故选:B.
总结提升:此题主要考查了反比例函数的应用,正确掌握反比例函数图象分布规律是解题关键.
3. (2023•鄂州一模)已知A、B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)a= ,b= .
(2)求甲、乙两车相遇后y与x之间的函数关系式.
(3)当甲车到达距B地90千米处时,求甲、乙两车之间的路程.
思路引领:(1)根据图象可知两车2小时后相遇,根据路程和为270千米即可求出乙车的速度;然后根据“路程、速度、时间”的关系确定a、b的值;
(2)运用待定系数法解得即可;
(3)求出甲车到达距B地90千米处时行驶的时间,代入(2)的结论解答即可.
解:(1)乙车的速度为:(270﹣60×2)÷2=75千米/时,
a=270÷75=3.6,b=270÷60=4.5.
故答案为:3.6;4.5;
(2)60×3.6=216(千米),
当2<x≤3.6时,设y=kx+b,根据题意得:
2k+b=03.6k+b=216,解得k=135b=−270,
∴y=135x﹣270(2<x≤3.6);
当3.6<x≤4.5时,y=60x,
∴y=135x−270(2<x≤3.6)60x(3.6<x≤4.5).
(3)∵甲车到达距B地90千米处时,x=270−9060=3,
∴将x=3代入y=135x﹣270,
得y=135×3﹣270=135,
即当甲车到达距B地90千米处时,甲、乙两车之间的路程是135千米.
总结提升:本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
4. (2023春•孝感期末)民生超市计划购进甲、乙两种商品共90件进行销售,有关信息如表,
设乙种商品有x(件),销售完两种商品的总销售额为y(元).
(1)求y与x的函数关系式;
(2)若购进乙种商品不超过45件,且该超市购进这两种商品的总进货费用不超过5000元.
①问共有多少种购进方案?
②直接写出总利润的最大值(总利润=总销售额﹣总进货费用).
思路引领:(1)分两种情况:当0≤x≤20时和当20<x≤90时,分别根据已知列出函数关系式即可;
(2)①由购进乙种商品不超过45件,且该超市购进这两种商品的总进货费用不超过5000元,得x≤4560(90−x)+50x≤5000,即可解得共有6种购进方案;
②设总利润为w元,可得w=(﹣20x+9400)﹣[60(90﹣x)+50x]=﹣10x+4000,由一次函数性质可得总利润的最大值是3600元.
解:(1)当0≤x≤20时,y=100(90﹣x)+100x=9000,
当20<x≤90时,y=100(90﹣x)+20×100+(100﹣20)×(x﹣20)=﹣20x+9400,
∴y=9000(0≤x≤20)−20x+9400(20<x≤90);
(2)①∵购进乙种商品不超过45件,且该超市购进这两种商品的总进货费用不超过5000元,
∴x≤4560(90−x)+50x≤5000,
解得40≤x≤45,
∵x是整数,
∴x可取40,41,42,43,44,45,
∴共有6种购进方案;
②设总利润为w元,
∵40≤x≤45,
∴总销售额y=﹣20x+9400,
∴w=(﹣20x+9400)﹣[60(90﹣x)+50x]=﹣10x+4000,
∵﹣10<0,
∴w随x的增大而减小,
∴x=40时,w取最大值,最大值为﹣10×40+4000=3600(元),
答:总利润的最大值是3600元.
总结提升:本题考查一次函数的应用,解题的关键是读懂题意,列出函数关系式.商品
甲
乙
进价(元/件)
60
50
售价(元/件)
100
100(其中一次性销售超过20件时,超出部分每件再让利20元)
相关试卷
这是一份中考数学二轮复习核心考点专题提优拓展训练专题13旋转中的全等模型(原卷版+解析),共30页。试卷主要包含了对角互补模型,手拉手模型——旋转全等,通过旋转构造三角形全等等内容,欢迎下载使用。
这是一份中考数学二轮复习核心考点专题提优拓展训练专题12含参代数式、方程与函数(原卷版+解析),共28页。试卷主要包含了含有参数的代数式,含有参数的方程,含有参数的函数等内容,欢迎下载使用。
这是一份中考数学二轮复习核心考点专题提优拓展训练专题11反比例函数与一次函数二次函数的综合运用(原卷版+解析),共22页。试卷主要包含了反比例函数与一次函数的综合运用,反比例函数与二次函数的综合运用等内容,欢迎下载使用。












