
所属成套资源:中考数学总复习精品专题(原卷版+解析)
中考数学总复习专题11反比例函数及其应用(10个高频考点)(举一反三)(全国版)(原卷版+解析)
展开
这是一份中考数学总复习专题11反比例函数及其应用(10个高频考点)(举一反三)(全国版)(原卷版+解析),共60页。
TOC \ "1-1" \h \u
\l "_Tc25828" 【考点1 反比例函数的定义】 PAGEREF _Tc25828 \h 1
\l "_Tc31524" 【考点2 反比例函数的图象】 PAGEREF _Tc31524 \h 2
\l "_Tc1224" 【考点3 反比例函数图象的对称性】 PAGEREF _Tc1224 \h 4
\l "_Tc6758" 【考点4 反比例函数的性质】 PAGEREF _Tc6758 \h 4
\l "_Tc15071" 【考点5 反比例函数系数k的几何意义】 PAGEREF _Tc15071 \h 5
\l "_Tc2730" 【考点6 反比例函数图象上点的坐标特征】 PAGEREF _Tc2730 \h 7
\l "_Tc18456" 【考点7 待定系数法求反比例函数解析式】 PAGEREF _Tc18456 \h 8
\l "_Tc2062" 【考点8 反比例函数与一次函数的综合】 PAGEREF _Tc2062 \h 9
\l "_Tc9052" 【考点9 实际问题与反比例函数】 PAGEREF _Tc9052 \h 10
\l "_Tc13330" 【考点10 反比例函数与几何综合】 PAGEREF _Tc13330 \h 13
【要点1 反比例函数的定义】
一般的,形如的函数,叫做反比例函数。其中是自变量,是函数。
自变量的取值范围是不等于0的一切实数
【要点2 反比例函数的解析式】
1、; 2、; 3、
【考点1 反比例函数的定义】
【例1】(2022·浙江·校考三模)图像经过点(1,2)的反比例函数是( )
A.y=−2xB.y=2xC.y=12xD.y=2x
【变式1-1】(2022·辽宁抚顺·统考二模)下列函数中,y是x的反比例函数的是( )
A.y=−x2B.y=1x2C.y=13xD.y=−12x
【变式1-2】(2022·北京石景山·统考一模)下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
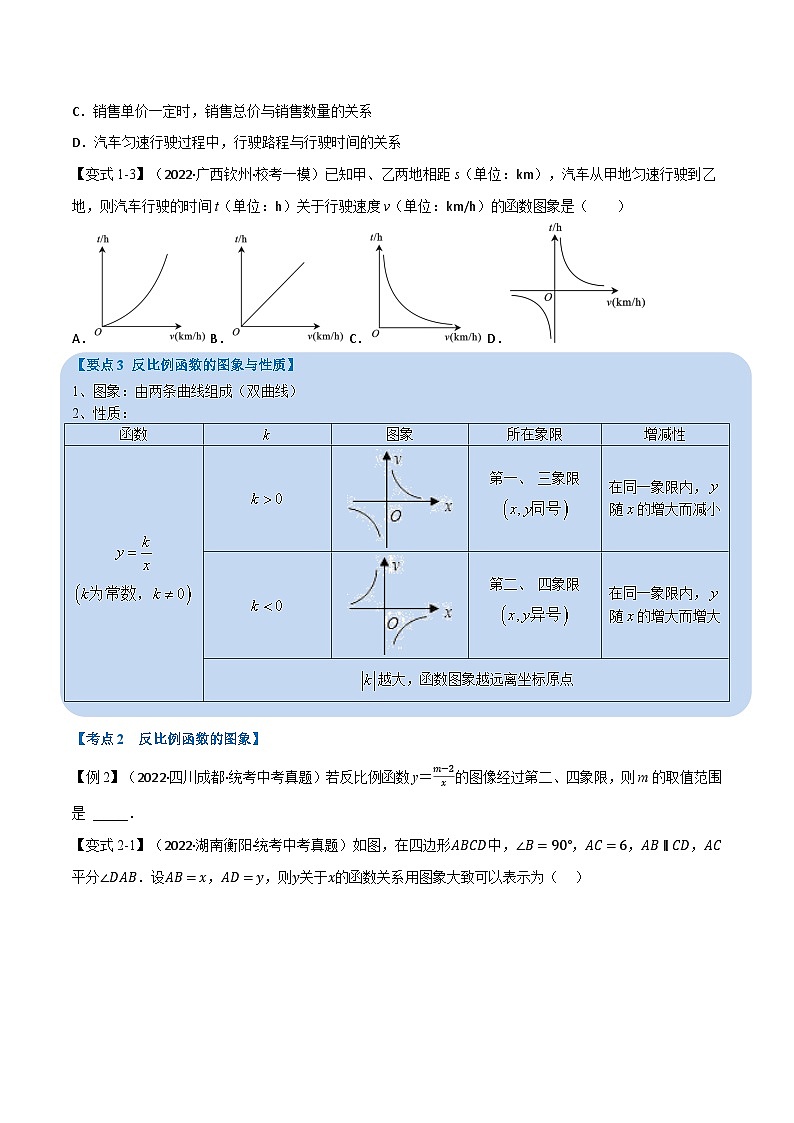
【变式1-3】(2022·广西钦州·校考一模)已知甲、乙两地相距s(单位:km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(单位:h)关于行驶速度v(单位:km/h)的函数图象是( )
A.B.C.D.
【要点3 反比例函数的图象与性质】
1、图象:由两条曲线组成(双曲线)
2、性质:
【考点2 反比例函数的图象】
【例2】(2022·四川成都·统考中考真题)若反比例函数y=m−2x的图像经过第二、四象限,则m的取值范围是 _____.
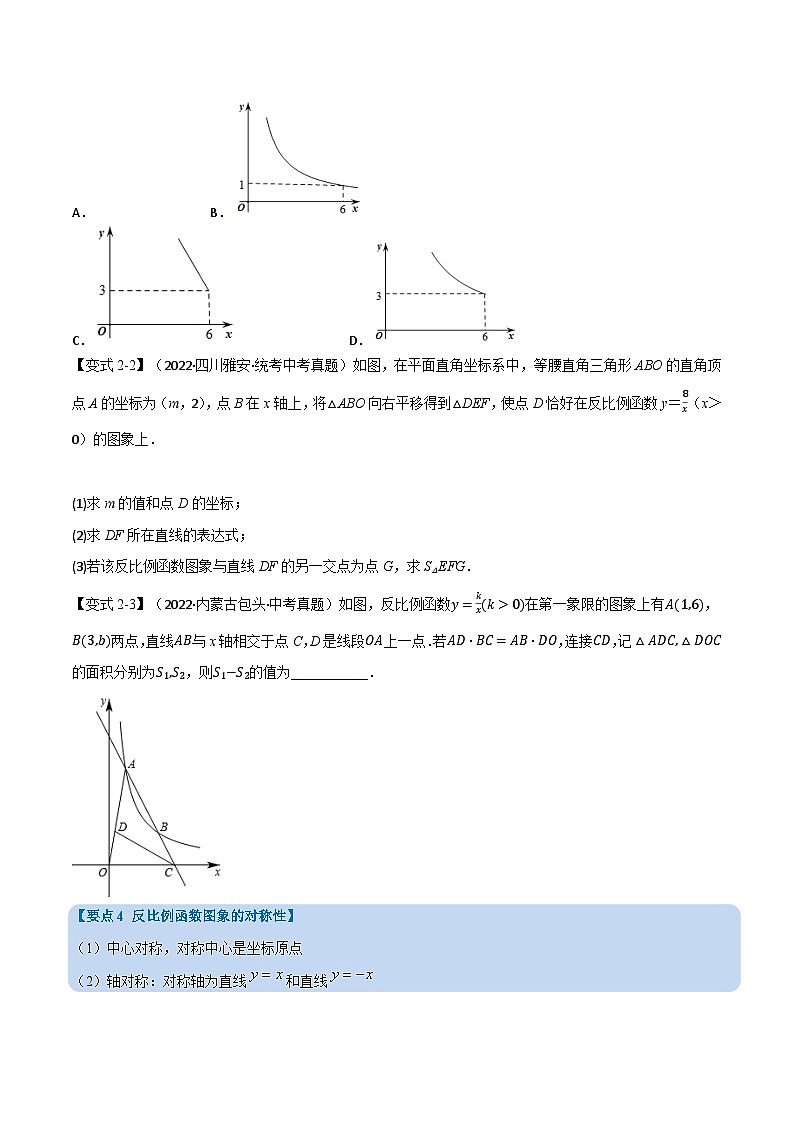
【变式2-1】(2022·湖南衡阳·统考中考真题)如图,在四边形ABCD中,∠B=90°,AC=6,AB∥CD,AC平分∠DAB.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
B.
C.D.
【变式2-2】(2022·四川雅安·统考中考真题)如图,在平面直角坐标系中,等腰直角三角形ABO的直角顶点A的坐标为(m,2),点B在x轴上,将△ABO向右平移得到△DEF,使点D恰好在反比例函数y=8x(x>0)的图象上.
(1)求m的值和点D的坐标;
(2)求DF所在直线的表达式;
(3)若该反比例函数图象与直线DF的另一交点为点G,求S△EFG.
【变式2-3】(2022·内蒙古包头·中考真题)如图,反比例函数y=kx(k>0)在第一象限的图象上有A(1,6),B(3,b)两点,直线AB与x轴相交于点C,D是线段OA上一点.若AD⋅BC=AB⋅DO,连接CD,记△ADC,△DOC的面积分别为S1,S2,则S1−S2的值为___________.
【要点4 反比例函数图象的对称性】
(1)中心对称,对称中心是坐标原点
(2)轴对称:对称轴为直线和直线
【考点3 反比例函数图象的对称性】
【例3】(2022·四川攀枝花·统考中考真题)如图,正比例函数y=k1x与反比例函数y=k2x的图像交于A(1,m)、B两点,当k1x≤k2x时,x的取值范围是( )
A.−1≤x0)上,且AD⊥x轴,CA的延长线交y轴于点E.若S△ABE=32,则k=______.
【考点6 反比例函数图象上点的坐标特征】
【例6】(2022·辽宁阜新·统考中考真题)已知反比例函数y=kxk≠0的图像经过点−2,4,那么该反比例函数图像也一定经过点( )
A.4,2B.1,8C.−1,8D.−1,−8
【变式6-1】(2022·江苏淮安·统考中考真题)在平面直角坐标系中,将点A2,3向下平移5个单位长度得到点B,若点B恰好在反比例函数y=kx的图像上,则k的值是______.
【变式6-2】(2022·广东深圳·统考中考真题)如图,已知直角三角形ABO中,AO=1,将△ABO绕点O点旋转至△A′B′O的位置,且A′在OB的中点,B′在反比例函数y=kx上,则k的值为________________.
【变式6-3】(2022·湖北武汉·统考中考真题)如图,OA=OB,∠AOB=90°,点A,B分别在函数y=k1x(x>0)和y=k2x(x>0)的图象上,且点A的坐标为(1,4).
(1)求k1,k2的值:
(2)若点C,D分在函数y=k1x(x>0)和y=k2x(x>0)的图象上,且不与点A,B重合,是否存在点C,D,使得△COD≌△AOB,若存在,请直接出点C,D的坐标:若不存在,请说明理由.
【考点7 待定系数法求反比例函数解析式】
【例7】(2022·山东威海·统考中考真题)正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=kx(k≠0)的图象经过点C,则k的值为 _____.
【变式7-1】(2022·山东淄博·统考中考真题)如图,直线y=kx+b与双曲线y=mx相交于A(1,2),B两点,与x轴相交于点C(4,0).
(1)分别求直线AC和双曲线对应的函数表达式;
(2)连接OA,OB,求△AOB的面积;
(3)直接写出当x>0时,关于x的不等式kx+b>mx的解集.
【变式7-2】(2022·青海西宁·统考中考真题)如图,正比例函数y=4x与反比例函数y=kxx>0的图象交于点Aa,4,点B在反比例函数图象上,连接AB,过点B作BC⊥x轴于点C2,0.
(1)求反比例函数解析式;
(2)点D在第一象限,且以A,B,C,D为顶点的四边形是平行四边形,请直接写出点D的坐标.
【变式7-3】(2022·黑龙江绥化·统考中考真题)在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A5,0,B0,52两点,且与反比例函数y2=k2x的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为54.
(1)求一次函数与反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.
【考点8 反比例函数与一次函数的综合】
【例8】(2022·西藏·统考中考真题)在同一平面直角坐标系中,函数y=ax+b与y=bax(其中a,b是常数,ab≠0)的大致图象是( )
A.B.C.D.
【变式8-1】(2022·四川巴中·统考中考真题)将双曲线y=1x向右平移2个单位,再向下平移1个单位,得到的新双曲线与直线y=ki(x−2)−1 ki>0,i=1,2,3,⋅⋅⋅,1011相交于2022个点,则这2022个点的横坐标之和为________.
【变式8-2】(2022·宁夏·中考真题)如图,一次函数y=kx+bk≠0的图象与x轴、y轴分别相交于C、B两点,与反比例函数y=mx(m≠0,x>0)的图象相交于点A,OB=1,tan∠OBC=2,BC:CA=1:2.
(1)求反比例函数的表达式;
(2)点D是线段AB上任意一点,过点D作y轴平行线,交反比例函数的图象于点E,连接BE.当△BDE面积最大时,求点D的坐标.
【变式8-3】(2022·江苏徐州·统考中考真题)如图,一次函数y=kx+b(k>0)的图像与反比例函数y=8x(x>0)的图像交于点A,与x轴交于点B,与y轴交于点C,AD⊥x轴于点D,CB=CD,点C关于直线AD的对称点为点E.
(1)点E是否在这个反比例函数的图像上?请说明理由;
(2)连接AE、DE,若四边形ACDE为正方形.
①求k、b的值;
②若点P在y轴上,当|PE−PB|最大时,求点P的坐标.
【考点9 实际问题与反比例函数】
【例9】(2022·山东枣庄·统考中考真题)为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
(1)在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?
【变式9-1】(2022·辽宁大连·统考中考真题)密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当V=5m3时,ρ=1.98kg/m3.
(1)求密度ρ关于体积V的函数解析式;
(2)若3≤V≤9,求二氧化碳密度ρ的变化范围.
【变式9-2】(2022·广东广州·统考中考真题)某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2) 与其深度d(单位:m)是反比例函数关系,它的图象如图所示.
(1)求储存室的容积V的值;
(2)受地形条件限制,储存室的深度d需要满足16≤d≤25,求储存室的底面积S的取值范围.
【变式9-3】(2022·山东临沂·统考中考真题)杠杆原理在生活中被广泛应用(杠杆原理:阻力×阻力臂=动力×动力臂),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图1).制作方法如下:
第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm),确定支点O,并用细麻绳固定,在支点O左侧2cm的A处固定一个金属吊钩,作为秤钩;
第二步:取一个质量为0.5kg的金属物体作为秤砣.
(1)图1中,把重物挂在秤钩上,秤砣挂在支点О右侧的B处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,OB的长度随之变化.设重物的质量为xkg,OB的长为ycm.写出y关于x的函数解析式;若0OC.
请解答下列问题:
(1)求点B,C的坐标;
(2)若反比例函数y=kxk≠0图象的一支经过点D,求这个反比例函数的解析式;
(3)平面内是否存在点M,N(M在N的上方),使以B,D,M,N为顶点的四边形是边长比为2:3的矩形?若存在,请直接写出在第四象限内点N的坐标;若不存在,请说明理由. 函数
图象
所在象限
增减性
三象限
在同一象限内,随的增大而减小
四象限
在同一象限内,随的增大而增大
越大,函数图象越远离坐标原点
时间x(天)
3
5
6
9
……
硫化物的浓度y(mg/L)
4.5
2.7
2.25
1.5
……
xkg
……
0.25
0.5
1
2
4
……
ycm
……
……
专题11 反比例函数及其应用(10个高频考点)(举一反三)
TOC \ "1-1" \h \u
\l "_Tc25828" 【考点1 反比例函数的定义】 PAGEREF _Tc25828 \h 1
\l "_Tc31524" 【考点2 反比例函数的图象】 PAGEREF _Tc31524 \h 3
\l "_Tc1224" 【考点3 反比例函数图象的对称性】 PAGEREF _Tc1224 \h 9
\l "_Tc6758" 【考点4 反比例函数的性质】 PAGEREF _Tc6758 \h 12
\l "_Tc15071" 【考点5 反比例函数系数k的几何意义】 PAGEREF _Tc15071 \h 14
\l "_Tc2730" 【考点6 反比例函数图象上点的坐标特征】 PAGEREF _Tc2730 \h 18
\l "_Tc18456" 【考点7 待定系数法求反比例函数解析式】 PAGEREF _Tc18456 \h 22
\l "_Tc2062" 【考点8 反比例函数与一次函数的综合】 PAGEREF _Tc2062 \h 29
\l "_Tc9052" 【考点9 实际问题与反比例函数】 PAGEREF _Tc9052 \h 36
\l "_Tc13330" 【考点10 反比例函数与几何综合】 PAGEREF _Tc13330 \h 42
【要点1 反比例函数的定义】
一般的,形如的函数,叫做反比例函数。其中是自变量,是函数。
自变量的取值范围是不等于0的一切实数
【要点2 反比例函数的解析式】
1、; 2、; 3、
【考点1 反比例函数的定义】
【例1】(2022·浙江·校考三模)图像经过点(1,2)的反比例函数是( )
A.y=−2xB.y=2xC.y=12xD.y=2x
【答案】B
【分析】将x=1代入到A、B、C函数关系式中求出y值即可找出答案,D中y=2x是正比例函数,不用考虑.
【详解】解:观察四个选项,A、B、C是反比函数,D是正比例函数,
将x=1代入到A、B、C函数关系式中,只有B选项中y=2,
故正确答案为:B.
【点睛】本题考查反比例函数上的点,熟练掌握反比例函数的定义是解题关键.
【变式1-1】(2022·辽宁抚顺·统考二模)下列函数中,y是x的反比例函数的是( )
A.y=−x2B.y=1x2C.y=13xD.y=−12x
【答案】D
【分析】根据反比例函数的定义即形如y=kx(k是常数,且k≠0)的函数,对各选项进行判断即可.
【详解】A选项中函数是正比例函数,故不符合题意;
B选项中函数不是反比例函数,故不符合题意;
C选项中函数是正比例函数,故不符合题意;
D选项中函数符合反比例函数的定义,故符合题意;
故选:D.
【点睛】本题考查了反比例函数的定义.解题的关键在于对反比例定义与形式的熟练掌握与灵活运用.
【变式1-2】(2022·北京石景山·统考一模)下列两个变量之间的关系为反比例关系的是( )
A.圆的周长与其半径的关系
B.平行四边形面积一定时,其一边长与这边上的高的关系
C.销售单价一定时,销售总价与销售数量的关系
D.汽车匀速行驶过程中,行驶路程与行驶时间的关系
【答案】B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【详解】A. 圆的周长与其半径是正比例关系,不符合题意,
B. 平行四边形面积一定时,其一边长与这边上的高成反比例关系,符合题意,
C. 销售单价一定时,销售总价与销售数量成正比例关系,不符合题意,
D. 汽车匀速行驶过程中,行驶路程与行驶时间成正比例关系,不符合题意,
故选B.
【点睛】本题主要考查成反比例函数关系的量,关键就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
【变式1-3】(2022·广西钦州·校考一模)已知甲、乙两地相距s(单位:km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(单位:h)关于行驶速度v(单位:km/h)的函数图象是( )
A.B.C.D.
【答案】C
【分析】根据实际意义,写出函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
【详解】解:根据题意有:v•t=s,
∴t=sv,
故t与v之间的函数图象为反比例函数图象,
且根据实际意义v>0、t>0,
∴其图像在第一象限,故C正确.
故选:C.
【点睛】本题主要考查了反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
【要点3 反比例函数的图象与性质】
1、图象:由两条曲线组成(双曲线)
2、性质:
【考点2 反比例函数的图象】
【例2】(2022·四川成都·统考中考真题)若反比例函数y=m−2x的图像经过第二、四象限,则m的取值范围是 _____.
【答案】m<2
【分析】由反比例函数图像经过第二、四象限,得出m﹣2<0,求出m范围即可.
【详解】解:∵反比例函数y=m−2x的图像经过第二、四象限,
∴m﹣2<0,
得:m<2.
故答案为:m<2.
【点睛】本题主要考查了反比例函数图像的性质,根据反比例函数图像的性质,列出关于m的不等式,是解题的关键.
【变式2-1】(2022·湖南衡阳·统考中考真题)如图,在四边形ABCD中,∠B=90°,AC=6,AB∥CD,AC平分∠DAB.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
B.
C.D.
【答案】D
【分析】先证明CD=AD=y,过D点做DE⊥AC于点E,证明△ABC∽△AED,利用相似三角形的性质可得函数关系式,从而可得答案.
【详解】解:∵AB∥CD,∴∠ACD=∠BAC,
∵AC平分∠DAB,∴∠BAC=∠CAD,
∴∠ACD=∠CAD,则CD=AD=y,即△ACD为等腰三角形,
过D点做DE⊥AC于点E.
则DE垂直平分AC,AE=CE=12AC=3,∠AED=90°,
∵∠BAC=∠CAD,∠B=∠AED=90°,
∴△ABC∽△AED,
∴ACAD=ABAE,
∴6y=x3,
∴y=18x,
∵在△ABC中,AB
相关试卷
这是一份中考数学总复习专题11反比例函数及其应用(10个高频考点)(强化训练)(全国版)(原卷版+解析),共91页。
这是一份中考数学总复习专题10一次函数及其应用(12个高频考点)(举一反三)(全国版)(原卷版+解析),共56页。
这是一份中考数学一轮复习高频考点专题11 反比例函数及其应用(10个高频考点)(举一反三)(2份打包,原卷版+解析版),文件包含中考数学一轮复习高频考点专题11反比例函数及其应用10个高频考点举一反三原卷版doc、中考数学一轮复习高频考点专题11反比例函数及其应用10个高频考点举一反三解析版doc等2份试卷配套教学资源,其中试卷共81页, 欢迎下载使用。








