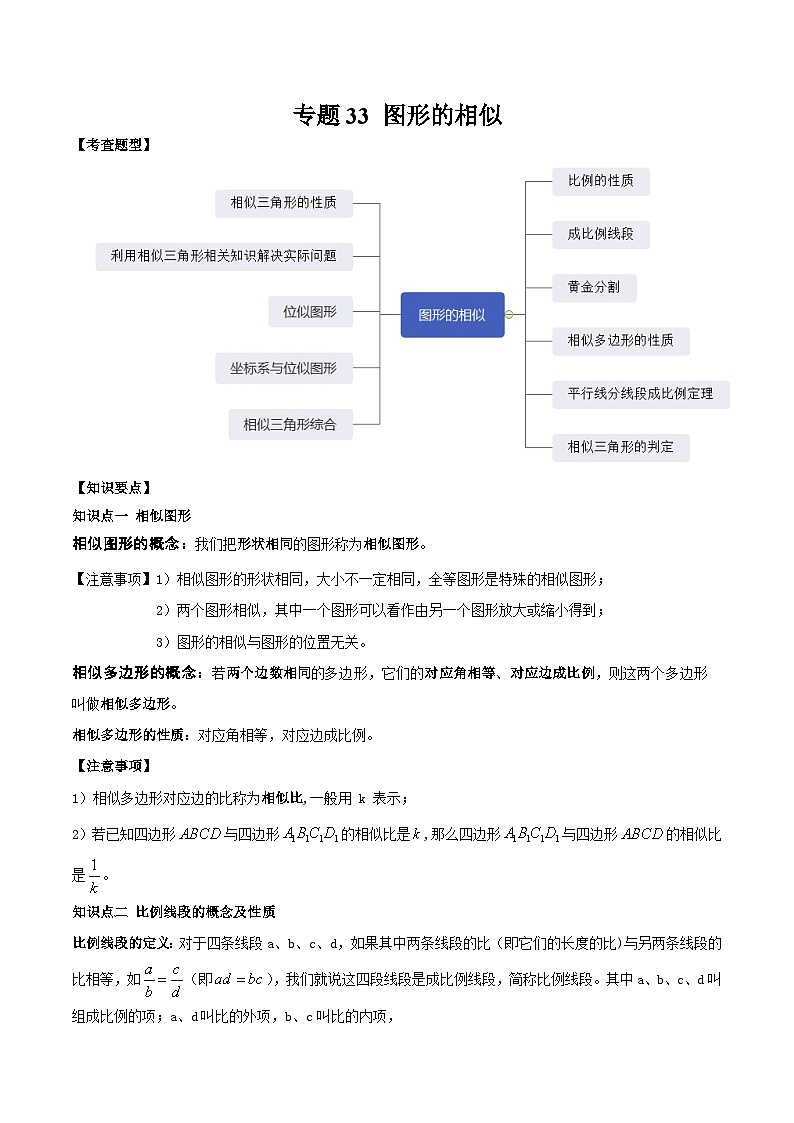
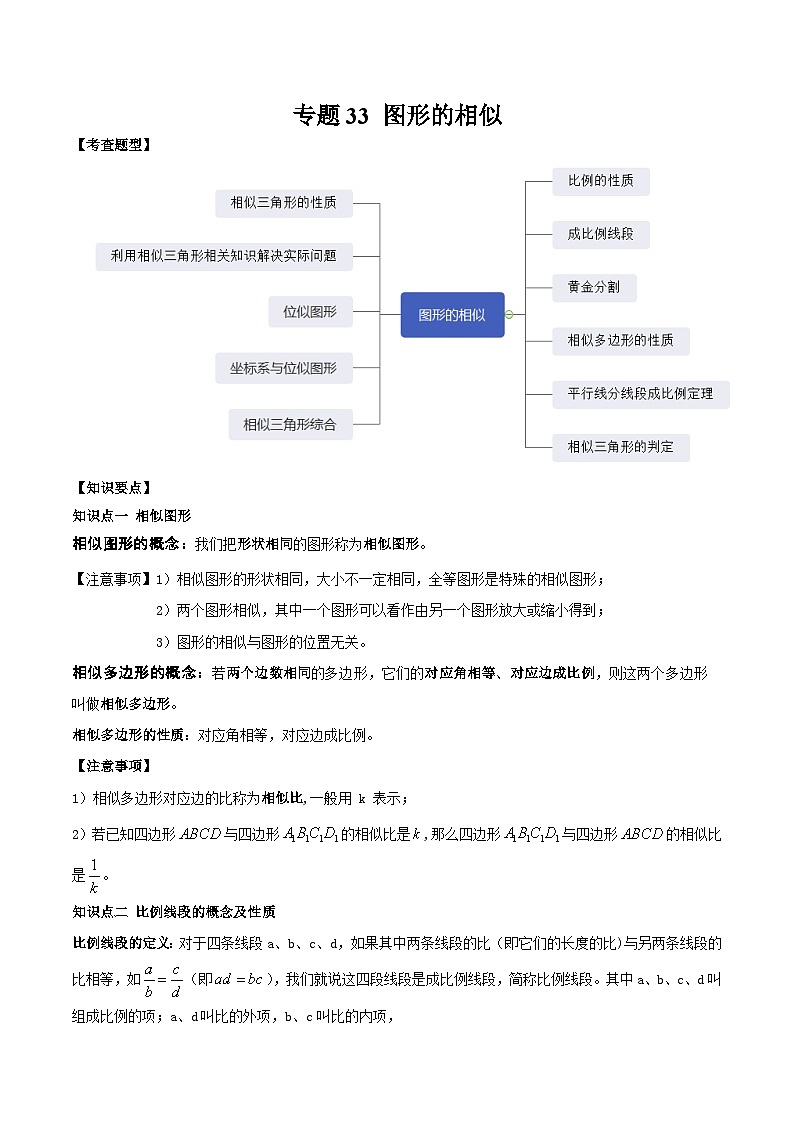
中考数学一轮复习满分突破考点题型专练专题33 图形的相似（2份打包，原卷版+解析版）

这是一份中考数学一轮复习满分突破考点题型专练专题33 图形的相似（2份打包，原卷版+解析版），文件包含中考数学一轮复习满分突破考点题型专练专题33图形的相似原卷版doc、中考数学一轮复习满分突破考点题型专练专题33图形的相似解析版doc等2份试卷配套教学资源，其中试卷共91页， 欢迎下载使用。


【知识要点】
知识点一 相似图形
相似图形的概念：我们把形状相同的图形称为相似图形。
【注意事项】1）相似图形的形状相同，大小不一定相同，全等图形是特殊的相似图形；
2）两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到；
3）图形的相似与图形的位置无关。
相似多边形的概念：若两个边数相同的多边形，它们的对应角相等、对应边成比例，则这两个多边形叫做相似多边形。
相似多边形的性质：对应角相等，对应边成比例。
【注意事项】
1）相似多边形对应边的比称为相似比,一般用 k 表示；
2）若已知四边形 SKIPIF 1 < 0 与四边形 SKIPIF 1 < 0 的相似比是 SKIPIF 1 < 0 ,那么四边形 SKIPIF 1 < 0 与四边形 SKIPIF 1 < 0 的相似比是 SKIPIF 1 < 0 。
知识点二 比例线段的概念及性质
比例线段的定义：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度的比)与另两条线段的比相等，如 SKIPIF 1 < 0 （即 SKIPIF 1 < 0 ），我们就说这四段线段是成比例线段，简称比例线段。其中a、b、c、d叫组成比例的项；a、d叫比的外项，b、c叫比的内项，
【补充】当比的内项相等时，即或a：b=b：d，线段 b 叫做线段a和d的比例中项。
【解题思路】
1）判断四条线段是否成比例，需要将这四条线段从小到大依次排列，再判断前两条线段的比与后两条线段的比是否相等即可；
2）成比例的线段是有顺序的，比如：a、b、c、d是成比例的线段，则成比例线段只能写成 SKIPIF 1 < 0 （即：），而不能写成 SKIPIF 1 < 0 。
比例的性质：
①基本性质： SKIPIF 1 < 0 SKIPIF 1 < 0
②变形： SKIPIF 1 < 0 核心内容： SKIPIF 1 < 0
③合、分比性质： SKIPIF 1 < 0
【注意】实际上，比例的合比性质可扩展为：比例式中等号左右两个比的前项，后项之间发生同样和差变化比例仍成立．如： SKIPIF 1 < 0
④等比性质：如果 SKIPIF 1 < 0 ， 那么 SKIPIF 1 < 0
⑤黄金分割：点C把线段AB分割成AC和CB两段,如果 SKIPIF 1 < 0 ,那么线段AB被点C黄金分割，点C叫做线段AB的黄金分割点，AC与AB的比叫做黄金比。
【注意】1） SKIPIF 1 < 0 ( SKIPIF 1 < 0 叫做黄金分割值). 简记为： SKIPIF 1 < 0
2）一条线段的黄金分割点有两个。
3）黄金三角形的概念：顶角是360的等腰三角形。
4）黄金矩形的概念：宽与长的比等于黄金数的矩形。
【扩展】作一条线段的黄金分割点：
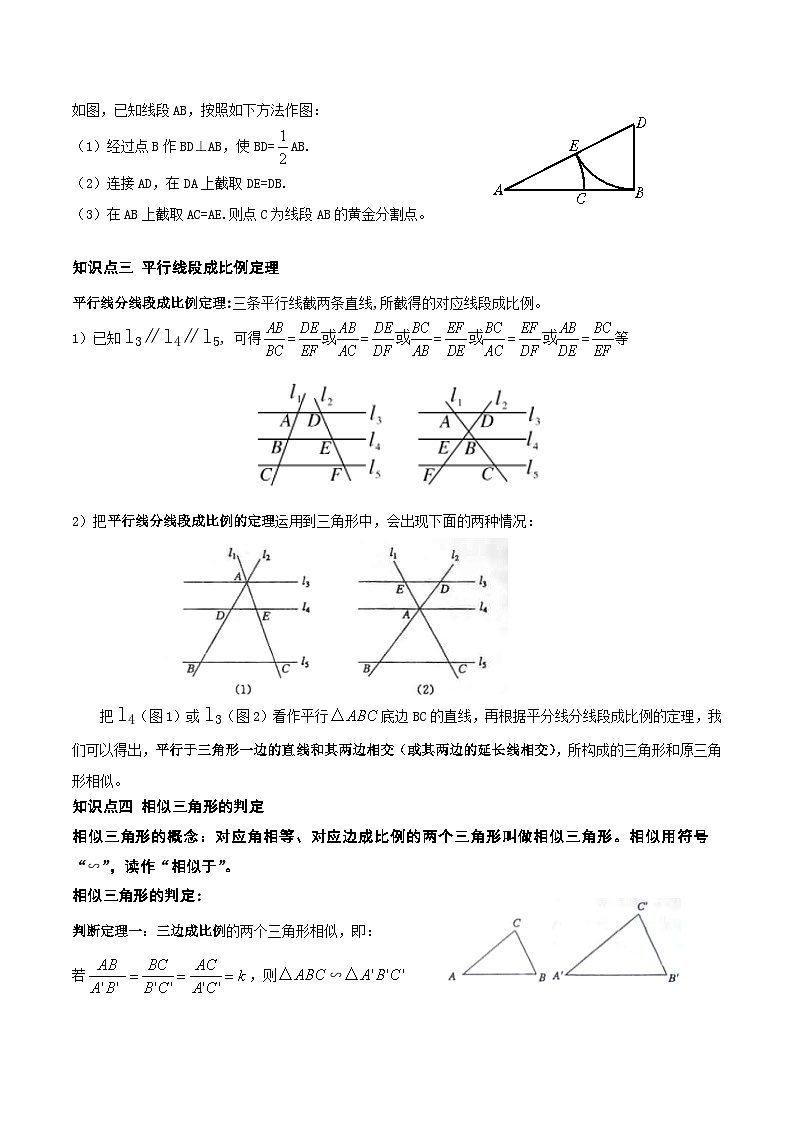
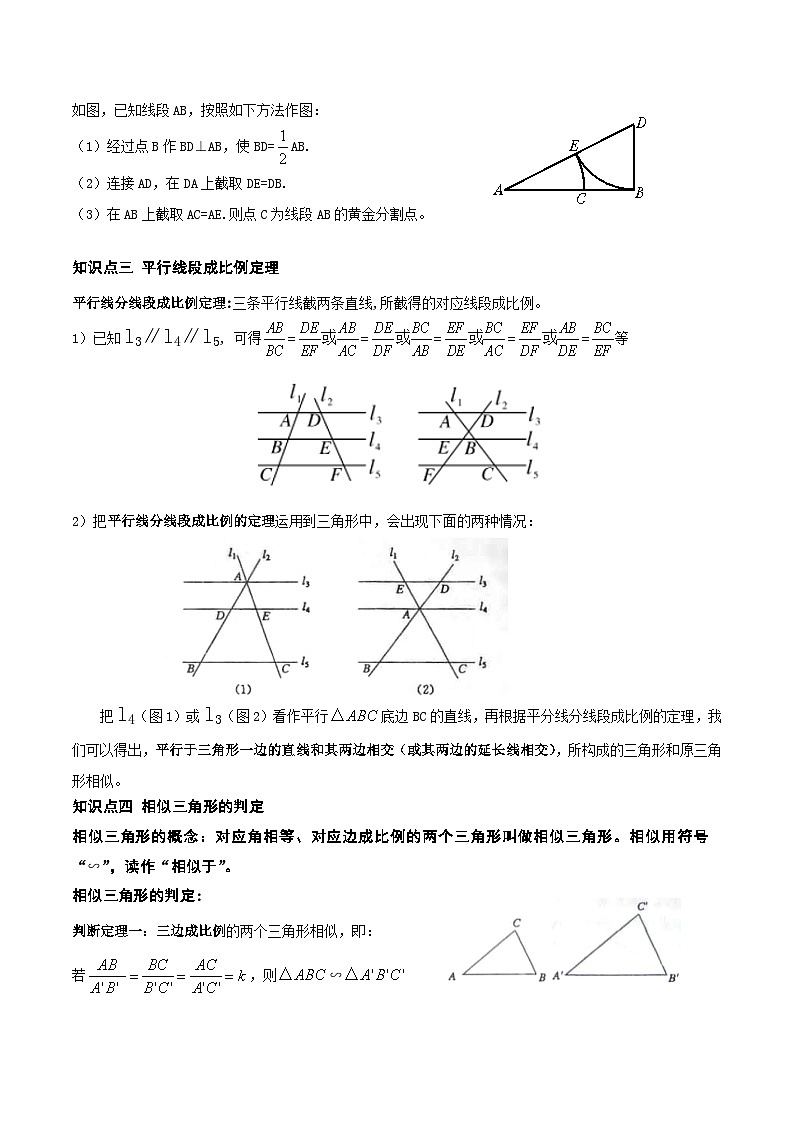
如图，已知线段AB，按照如下方法作图：
（1）经过点B作BD⊥AB，使BD= SKIPIF 1 < 0 AB.
（2）连接AD，在DA上截取DE=DB.
（3）在AB上截取AC=AE.则点C为线段AB的黄金分割点。
知识点三 平行线段成比例定理
平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例。
1）已知l3∥l4∥l5, 可得 SKIPIF 1 < 0 等
2）把平行线分线段成比例的定理运用到三角形中，会出现下面的两种情况：
把l4（图1）或l3（图2）看作平行 SKIPIF 1 < 0 底边BC的直线，再根据平分线分线段成比例的定理，我们可以得出，平行于三角形一边的直线和其两边相交（或其两边的延长线相交），所构成的三角形和原三角形相似。
知识点四 相似三角形的判定
相似三角形的概念：对应角相等、对应边成比例的两个三角形叫做相似三角形。相似用符号“∽”，读作“相似于”。
相似三角形的判定:
判断定理一：三边成比例的两个三角形相似，即：
若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ∽ SKIPIF 1 < 0
【技巧】判断网格中三角形是否相似，先运用勾股定理计算出三边的长度，再看对应边的比例是否相等。
判断定理二：两边成比例并且夹角相等的两个三角形相似。
即：若 SKIPIF 1 < 0 ，且∠C＝ SKIPIF 1 < 0 则 SKIPIF 1 < 0 ∽ SKIPIF 1 < 0
判断定理三：两个角分别相等的两个三角形相似。
即：若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ∽ SKIPIF 1 < 0
判断定理四：斜边和直角边成比例的两个直角三角形相似。
即：在 SKIPIF 1 < 0 中，
若 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ,
则 SKIPIF 1 < 0
【小结】
【常见的相似三角形】见附件pdf
知识点五 相似三角形的性质
1）相似三角形的对应角相等，对应边的比相等。
2）相似三角形对应高，对应中线，对应角平分线的比都等于相似比。
3）相似三角形周长的比等于相似比。
4）相似三角形面积比等于相似比的平方。
知识点六 位似
位似图形的定义: 如果两个图形不仅是相似图形,且对应点连线相交于一点,对应线段相互平行,那么这样的两个图形叫做位似图形,位似图形对应点连线的交点是位似中心。
【注意事项】1）位似图形是相似图形的一种特殊形式。
2）位似图形一定是相似图形，具有相似图形的所有性质，但相似图形不一定是位似图形。
常见的位似图形：
画位似图形的方法：两个位似图形可能位于位似中心的两侧，也可能位于位似中心的同侧。（即画位似图形时，注意关于某点的位似图形有两个。）
判断位似图形的方法：首先看这两个图形是否相似，再看对应点的连线是否经过位似中心。
位似图形的性质：
1)位似图形的对应顶点的连线所在直线相交与一点，位似图形的对应边互相平行或者共线。
2)位似图形上任意一对对应点到位似中心的距离之比等于相似比。
3)在平面直角坐标系中，如果以原点为位似中心，画一个与原图形的位似图形，使它与原图形的相似比为k，若原图形上点的坐标为(x，y)，则位似图形上与它对应的点的坐标为(kx，ky)或(-kx，-ky) 。
画位似图形的步骤：
1）确定位似中心,找原图形的关键点。
2）确定位似比。
3）以位似中心为端点向各关键点作射线。
4）顺次连结各截取点，即可得到要求的新图形。
平移、轴对称、旋转、位似的区别：
平移：和原图形一模一样 （和原图形全等且能与原图形重合）
轴对称：面积和原图形一样 也是全等，和平移的不同点就是轴对称之后的图形不能与原图形重合，虽然它们全等）
旋转：面积和原图形一样，也是全等，和轴对称的不同点是轴对称只有一个和原图形轴对称的图形，而旋转可以旋转出无数个。
位似：位似出的图形只和原图形的角相等 边就不一定相等了。
【总结】
考查题型一 比例的性质
典例1．（2022·江苏镇江·统考中考真题）《九章算术》中记载，战国时期的铜衡杆，其形式既不同于天平衡杆，也异于称杆衡杆正中有拱肩提纽和穿线孔，一面刻有贯通上、下的十等分线．用该衡杆称物，可以把被称物与砝码放在提纽两边不同位置的刻线上，这样，用同一个砝码就可以称出大于它一倍或几倍重量的物体．图为铜衡杆的使用示意图，此时被称物重量是砝码重量的_________倍．
变式1-1．（2021·黑龙江大庆·统考中考真题）已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ________
变式1-3．（2021·四川内江·统考中考真题）已知非负实数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ，最小值为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为 __．
考查题型二 成比例线段
典例2．（2022·湖南衡阳·统考中考真题）在设计人体雕像时，使雕像上部（腰部以上）与下部（腰部以下）的高度比，等于下部与全部的高度比，可以增加视觉美感．如图，按此比例设计一座高度为 SKIPIF 1 < 0 的雷锋雕像，那么该雕像的下部设计高度约是（ ）（结果精确到 SKIPIF 1 < 0 ．参考数据： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
变式2-1．（2021·四川德阳·统考中考真题）我们把宽与长的比是 SKIPIF 1 < 0 的矩形叫做黄金矩形．黄金矩形给我们以协调、匀称的美感，世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计．已知四边形ABCD是黄金矩形，边AB的长度为 SKIPIF 1 < 0 1，则该矩形的周长为 __________________．
变式2-2．（2022·湖南常德·统考中考真题）在四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 的平分线 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ，延长 SKIPIF 1 < 0 到 SKIPIF 1 < 0 使 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ．
(1)当四边形 SKIPIF 1 < 0 是矩形时，如图，求证：① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ．
(2)当四边形 SKIPIF 1 < 0 是平行四边形时，如图，（1）中的结论都成立，请给出结论②的证明．
考查题型三 黄金分割
典例3．（2022·山西·中考真题）神奇的自然界处处蕴含着数学知识．动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为0.618．这体现了数学中的（ ）
A．平移B．旋转C．轴对称D．黄金分割
变式3-1（2021·四川巴中·统考中考真题）两千多年前，古希腊数学家欧多克索斯发现了黄金分割，即：如图，点P是线段AB上一点（AP＞BP），若满足 SKIPIF 1 < 0 ，则称点P是AB的黄金分割点．黄金分割在日常生活中处处可见，例如：主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好．若舞台长20米，主持人从舞台一侧进入，设他至少走x米时恰好站在舞台的黄金分割点上，则x满足的方程是（ ）
A．（20﹣x）2＝20xB．x2＝20（20﹣x）
C．x（20﹣x）＝202D．以上都不对
变式3-2（2020·甘肃金昌·统考中考真题）生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下 SKIPIF 1 < 0 与全身 SKIPIF 1 < 0 的高度比值接近0．618，可以增加视觉美感，若图中 SKIPIF 1 < 0 为2米，则 SKIPIF 1 < 0 约为（ ）
A．1．24米B．1．38米C．1．42米D．1．62米
变式3-3（2022·湖北黄石·统考中考真题）如图，圆中扇子对应的圆心角 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ）与剩余圆心角 SKIPIF 1 < 0 的比值为黄金比时，扇子会显得更加美观，若黄金比取0.6，则 SKIPIF 1 < 0 的度数是__________．
变式3-4（2022·陕西·统考中考真题）在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果．如图，利用黄金分割法，所做 SKIPIF 1 < 0 将矩形窗框 SKIPIF 1 < 0 分为上下两部分，其中E为边 SKIPIF 1 < 0 的黄金分割点，即 SKIPIF 1 < 0 ．已知 SKIPIF 1 < 0 为2米，则线段 SKIPIF 1 < 0 的长为______米．
考查题型四 相似多边形的性质
典例4．（2022·广西梧州·统考中考真题）如图，以点O为位似中心，作四边形 SKIPIF 1 < 0 的位似图形 SKIPIF 1 < 0 ﹐已知 SKIPIF 1 < 0 ，若四边形 SKIPIF 1 < 0 的面积是2，则四边形 SKIPIF 1 < 0 的面积是（ ）
A．4B．6C．16D．18
变式4-1（2021·广西百色·统考中考真题）下列四个命题：①直径是圆的对称轴；②若两个相似四边形的相似比是1：3，则它们的周长比是1：3，面积比是1：6；③同一平面内垂直于同一直线的两条直线互相平行；④对角线相等且互相垂直的平行四边形是正方形．其中真命题有（ ）
A．①③B．①④C．③④D．②③④
变式4-2（2021·黑龙江牡丹江·统考中考真题）如图，矩形OABC的面积为36，它的对角线OB与双曲线y SKIPIF 1 < 0 相交于点D，且OD：OB＝2：3，则k的值为（ ）
A．12B．﹣12C．16D．﹣16
考查题型五 平行线分线段成比例定理
典例5（2022·四川巴中·统考中考真题）如图，在平面直角坐标系中， SKIPIF 1 < 0 为 SKIPIF 1 < 0 的 SKIPIF 1 < 0 边上一点， SKIPIF 1 < 0 ，过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 、 SKIPIF 1 < 0 两点纵坐标分别为1、3，则 SKIPIF 1 < 0 点的纵坐标为（ ）
A．4B．5C．6D．7
变式5-1（2022·山东东营·统考中考真题）如图，点D为 SKIPIF 1 < 0 边 SKIPIF 1 < 0 上任一点， SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点E，连接 SKIPIF 1 < 0 相交于点F，则下列等式中不成立的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
变式5-2（2022·浙江丽水·统考中考真题）如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段 SKIPIF 1 < 0 ，则线段 SKIPIF 1 < 0 的长是（ ）
A． SKIPIF 1 < 0 B．1C． SKIPIF 1 < 0 D．2
变式5-3（2021·广西贵港·统考中考真题）如图，在正方形ABCD中，E，F是对角线AC上的两点，且EF＝2AE＝2CF，连接DE并延长交AB于点M，连接DF并延长交BC于点N，连接MN，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．1D． SKIPIF 1 < 0
变式5-4（2022·湖北襄阳·统考中考真题）如图，在△ABC中，D是AC的中点，△ABC的角平分线AE交BD于点F，若BF：FD＝3：1，AB+BE＝3 SKIPIF 1 < 0 ，则△ABC的周长为_____．
变式5-5（2022·上海·统考中考真题）如图，在△ABC中，∠A=30°，∠B=90°，D为AB中点，E在线段AC上， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 _____．
变式5-6（2021·辽宁锦州·统考中考真题）如图，在平面直角坐标系中，▱OABC的顶点A，B在第一象限内，顶点C在y轴上，经过点A的反比例函数y＝ SKIPIF 1 < 0 （x＞0）的图象交BC于点D．若CD＝2BD，▱OABC的面积为15，则k的值为______．
考查题型六 相似三角形的判定
典例6．（2022·山东菏泽·统考中考真题）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，E是边AC上一点，且 SKIPIF 1 < 0 ，过点A作BE的垂线，交BE的延长线于点D，求证： SKIPIF 1 < 0 ．
变式6-1（2022·江苏盐城·统考中考真题）如图，在 SKIPIF 1 < 0 与 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别在边 SKIPIF 1 < 0 、 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 ，若___________，则 SKIPIF 1 < 0 ．请从① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 这三个选项中选择一个作为条件（写序号），并加以证明．
变式6-2（2022·山东泰安·统考中考真题）如图，矩形 SKIPIF 1 < 0 中，点E在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交于点O． SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交于点F．
(1)若 SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ，求证： SKIPIF 1 < 0 ；
(2)找出图中与 SKIPIF 1 < 0 相似的三角形，并说明理由;
(3)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的长度．
变式6-3（2020·广西柳州·统考中考真题）如图，AB为⊙O的直径，C为⊙O上的一点，连接AC、BC，OD⊥BC于点E，交⊙O于点D，连接CD、AD，AD与BC交于点F，CG与BA的延长线交于点G．
（1）求证：△ACD∽△CFD；
（2）若∠CDA＝∠GCA，求证：CG为⊙O的切线；
（3）若sin∠CAD＝ SKIPIF 1 < 0 ，求tan∠CDA的值．
变式6-4（2020·湖北荆州·统考中考真题）如图矩形ABCD中，AB=20，点E是BC上一点，将 SKIPIF 1 < 0 沿着AE折叠，点B刚好落在CD边上的点G处，点F在DG上，将 SKIPIF 1 < 0 沿着AF折叠，点D刚好落在AG上点H处，此时 SKIPIF 1 < 0 ．
（1）求证： SKIPIF 1 < 0
（2）求AD的长；
（3）求 SKIPIF 1 < 0 的值．
考查题型七 相似三角形的性质
典例7．（2022·甘肃兰州·统考中考真题）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A．4B．6C．8D．16
变式7-1（2022·云南·中考真题）如图，在 SKIPIF 1 < 0 ABC中，D、E分别为线段BC、BA的中点，设 SKIPIF 1 < 0 ABC的面积为S SKIPIF 1 < 0 ， SKIPIF 1 < 0 EBD的面积为S SKIPIF 1 < 0 ．则 SKIPIF 1 < 0 =（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
变式7-2（2022·江苏连云港·统考中考真题） SKIPIF 1 < 0 的三边长分别为2，3，4，另有一个与它相似的三角形 SKIPIF 1 < 0 ，其最长边为12，则 SKIPIF 1 < 0 的周长是（ ）
A．54B．36C．27D．21
变式7-3（2022·山东威海·统考中考真题）由12个有公共顶点O的直角三角形拼成如图所示的图形，∠AOB＝∠BOC＝∠COD＝…＝∠LOM＝30°．若S△AOB＝1，则图中与△AOB位似的三角形的面积为( )
A．（ SKIPIF 1 < 0 ）3B．（ SKIPIF 1 < 0 ）7C．（ SKIPIF 1 < 0 ）6D．（ SKIPIF 1 < 0 ）6
变式7-4．（2022·湖南常德·统考中考真题）如图，已知 SKIPIF 1 < 0 是 SKIPIF 1 < 0 内的一点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 的面积为2， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的面积是________．
变式7-5（2022·浙江杭州·统考中考真题）如图，在 SKIPIF 1 < 0 ABC中，点D，E，F分别在边AB，AC，BC上，连接DE，EF，已知四边形BFED是平行四边形， SKIPIF 1 < 0 ．
(1)若 SKIPIF 1 < 0 ，求线段AD的长．
(2)若 SKIPIF 1 < 0 的面积为1，求平行四边形BFED的面积．
考查题型八 利用相似三角形相关知识解决实际问题
典例8．（2022·湖北十堰·统考中考真题）如图，某零件的外径为10cm，用一个交叉卡钳（两条尺长AC和BD相等）可测量零件的内孔直径AB．如果OA：OC=OB：OD=3，且量得CD=3cm，则零件的厚度x为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
变式8-1（2022·广西贺州·统考中考真题）某餐厅为了追求时间效率，推出一种液体“沙漏”免单方案（即点单完成后，开始倒转“沙漏”， “沙漏”漏完前，客人所点的菜需全部上桌，否则该桌免费用餐）．“沙漏”是由一个圆锥体和一个圆柱体相通连接而成．某次计时前如图（1）所示，已知圆锥体底面半径是 SKIPIF 1 < 0 ，高是 SKIPIF 1 < 0 ；圆柱体底面半径是 SKIPIF 1 < 0 ，液体高是 SKIPIF 1 < 0 ．计时结束后如图（2）所示，求此时“沙漏”中液体的高度为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
变式8-2（2022·江苏盐城·统考中考真题）“跳眼法”是指用手指和眼睛估测距离的方法
步骤：
第一步：水平举起右臂，大拇指紧直向上，大臂与身体垂直；
第二步：闭上左眼，调整位置，使得右眼、大拇指、被测物体在一条直线上；
第三步：闭上右眼，睁开左眼，此时看到被测物体出现在大拇指左侧，与大拇指指向的位置有一段横向距离，参照被测物体的大小，估算横向距离的长度；
第四步：将横向距离乘以10（人的手臂长度与眼距的比值一般为10），得到的值约为被测物体离观测，点的距离值．
如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图，该汽车的长度大约为4米，则汽车到观测点的距离约为（ ）
A．40米B．60米C．80米D．100米
变式8-3（2022·广西·中考真题）数学兴趣小组通过测量旗杆的影长来求旗杆的高度，他们在某一时刻测得高为2米的标杆影长为1.2米，此时旗杆影长为7.2米，则旗杆的高度为______米．
变式8-4（2022·广西·统考中考真题）古希腊数学家泰勒斯曾利用立杆测影的方法，在金字塔影子的顶部直立一根木杆，借助太阳光测金字塔的高度．如图，木杆EF长2米，它的影长FD是4米，同一时刻测得OA是268米，则金字塔的高度BO是________米．
变式8-5（2022·江苏徐州·统考中考真题）如图，公园内有一个垂直于地面的立柱AB，其旁边有一个坡面 SKIPIF 1 < 0 ，坡角 SKIPIF 1 < 0 ．在阳光下，小明观察到在地面上的影长为 SKIPIF 1 < 0 ，在坡面上的影长为 SKIPIF 1 < 0 ．同一时刻，小明测得直立于地面长60cm的木杆的影长为90cm（其影子完全落在地面上）．求立柱AB的高度．
变式8-6（2022·内蒙古鄂尔多斯·统考中考真题）旗杆及升旗台的剖面如图所示，MN、CD为水平线，旗杆AB⊥CD于点B．某一时刻，旗杆AB的一部分影子BD落在CD上，另一部分影子DE落在坡面DN上，已知BD＝1.2m，DE＝1.4m．同一时刻，测得竖直立在坡面DN上的1m高的标杆影长为0.25m（标杆影子在坡面DN上），此时光线AE与水平线的夹角为80.5°，求旗杆AB的高度．（参考数据：sin80.5°≈0.98，cs80.5°≈0.17，tan80.5°≈6）
变式8-7 （2022·上海·统考中考真题）我们经常会采用不同方法对某物体进行测量，请测量下列灯杆AB的长．
(1)如图1所示，将一个测角仪放置在距离灯杆AB底部a米的点D处，测角仪高为b米，从C点测得A点的仰角为α，求灯杆AB的高度．（用含a，b，ａ的代数式表示）
(2)我国古代数学家赵爽利用影子对物体进行测量的方法，在至今仍有借鉴意义图2所示，现将一高度为2米的木杆CG放在灯杆AB前，测得其影长CH为1米，再将木杆沿着BC方向移动1.8米至DE的位置，此时测得其影长DF为3米，求灯杆AB的高度
变式8-8（2022·江苏连云港·统考中考真题）我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔，是苏北地区现存最高和最古老的宝塔．小明与小亮要测量阿育王塔的高度，如图所示，小明在点 SKIPIF 1 < 0 处测得阿育王塔最高点 SKIPIF 1 < 0 的仰角 SKIPIF 1 < 0 ，再沿正对阿育王塔方向前进至 SKIPIF 1 < 0 处测得最高点 SKIPIF 1 < 0 的仰角 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；小亮在点 SKIPIF 1 < 0 处竖立标杆 SKIPIF 1 < 0 ，小亮的所在位置点 SKIPIF 1 < 0 、标杆顶 SKIPIF 1 < 0 、最高点 SKIPIF 1 < 0 在一条直线上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．（注：结果精确到 SKIPIF 1 < 0 ，参考数据： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）
(1)求阿育王塔的高度 SKIPIF 1 < 0 ；
(2)求小亮与阿育王塔之间的距离 SKIPIF 1 < 0 ．
考查题型九 位似图形
典例9．（2022·宁夏·中考真题）如图，将三角尺直立举起靠近墙面，打开手机手电筒照射三角尺，在墙面上形成影子．则三角尺与影子之间属于以下哪种图形变换（ ）
A．平移B．轴对称C．旋转D．位似
变式9-1（2022·广西·中考真题）已知△ABC与△A1B1C1是位似图形，位似比是1：3，则△ABC与△A1B1C1的面积比（ ）
A．1 ：3B．1：6C．1：9D．3：1
变式9-2（2022·重庆·统考中考真题）如图， SKIPIF 1 < 0 与 SKIPIF 1 < 0 位似，点O是它们的位似中心，且位似比为1∶2，则 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的周长之比是（ ）
A．1∶2B．1∶4C．1∶3D．1∶9
变式9-3（2022·四川成都·统考中考真题）如图， SKIPIF 1 < 0 和 SKIPIF 1 < 0 是以点 SKIPIF 1 < 0 为位似中心的位似图形．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的周长比是_________．
考查题型十 坐标系与位似中心
典例10．（2021·山东东营·统考中考真题）如图， SKIPIF 1 < 0 中，A、B两个顶点在x轴的上方，点C的坐标是（1，0），以点C为位似中心，在x轴的下方作 SKIPIF 1 < 0 的位似图形 SKIPIF 1 < 0 ，并把 SKIPIF 1 < 0 的边长放大到原来的2倍，设点B的横坐标是a，则点B的对应点 SKIPIF 1 < 0 的横坐标是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
变式10-1（2021·重庆·统考中考真题）如图，在平面直角坐标系中，将 SKIPIF 1 < 0 以原点O为位似中心放大后得到 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的相似比是（ ）
A．2：1B．1：2C．3：1D．1：3
变式10-2（2021·浙江嘉兴·统考中考真题）如图，在直角坐标系中， SKIPIF 1 < 0 与 SKIPIF 1 < 0 是位似图形，则位似中心的坐标为__________________．
变式10-3（2022·广西河池·统考中考真题）如图、在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（4，1），B（2，3），C（1，2）．
(1)画出与△ABC关于y轴对称的△A1B1C1；
(2)以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为 SKIPIF 1 < 0 ，并写出点B2的坐标．
考查题型十一 相似三角形综合
典例11．（2021·四川乐山·统考中考真题）在等腰 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 边上一点（不与点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 重合），连结 SKIPIF 1 < 0 ．
（1）如图1，若 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 的对称点为点 SKIPIF 1 < 0 ，结 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ________；
（2）若 SKIPIF 1 < 0 ，将线段 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 顺时针旋转 SKIPIF 1 < 0 得到线段 SKIPIF 1 < 0 ，连结 SKIPIF 1 < 0 ．
①在图2中补全图形；
②探究 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的数量关系，并证明；
（3）如图3，若 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，试探究 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 之间满足的数量关系，并证明．
变式11-1（2021·湖南岳阳·统考中考真题）如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点，连接 SKIPIF 1 < 0 ，将线段 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 顺时针旋转 SKIPIF 1 < 0 得到线段 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 交线段 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的平分线 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．
（1）如图1，若 SKIPIF 1 < 0 ，则线段 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的数量关系是________， SKIPIF 1 < 0 ________；
（2）如图2，在（1）的条件下，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
①试判断四边形 SKIPIF 1 < 0 的形状，并说明理由；
②求证： SKIPIF 1 < 0 ；
（3）如图3，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，请直接写出 SKIPIF 1 < 0 的值（用含 SKIPIF 1 < 0 的式子表示）．
变式11-2（2021·安徽·统考中考真题）如图1，在四边形ABCD中， SKIPIF 1 < 0 ，点E在边BC上，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 交线段AE于点F，连接BF．
（1）求证： SKIPIF 1 < 0 ；
（2）如图2，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求BE的长；
（3）如图3，若BF的延长线经过AD的中点M，求 SKIPIF 1 < 0 的值．
变式11-3（2021·内蒙古赤峰·统考中考真题）数学课上，有这样一道探究题．
如图，已知 SKIPIF 1 < 0 中，AB=AC=m，BC=n， SKIPIF 1 < 0 ，点P为平面内不与点A、C重合的任意一点，将线段CP绕点P顺时针旋转a，得线段PD，E、F分别是CB、CD的中点，设直线AP与直线EF相交所成的较小角为β，探究 SKIPIF 1 < 0 的值和 SKIPIF 1 < 0 的度数与m、n、α的关系，请你参与学习小组的探究过程，并完成以下任务：
（1）填空：
【问题发现】
小明研究了 SKIPIF 1 < 0 时，如图1，求出了 SKIPIF 1 < 0 ___________， SKIPIF 1 < 0 ___________；
小红研究了 SKIPIF 1 < 0 时，如图2，求出了 SKIPIF 1 < 0 ___________， SKIPIF 1 < 0 ___________；
【类比探究】
他们又共同研究了α=120°时，如图3，也求出了 SKIPIF 1 < 0 ；
【归纳总结】
最后他们终于共同探究得出规律： SKIPIF 1 < 0 __________(用含m、n的式子表示)； SKIPIF 1 < 0 ___________ (用含α的式子表示)．
（2）求出 SKIPIF 1 < 0 时 SKIPIF 1 < 0 的值和 SKIPIF 1 < 0 的度数．
三角形全等
三角形相似
两角夹一边对应相等(ASA)
两角一对边对应相等(AAS)
两边及夹角对应相等(SAS)
三边对应相等(SSS)、
斜边和一直角边相等(HL）
两角对应相等
两边对应成比例，且夹角相等
三边对应成比例
斜边和一直角边对应成比例
平移
轴对称
旋转
位似
原图形
全等
全等
全等
相似