初中数学19.3 矩形 菱形 正方形示范课ppt课件

这是一份初中数学19.3 矩形 菱形 正方形示范课ppt课件，共33页。PPT课件主要包含了逐点导讲练，课堂小结，作业提升，学习目标，课时讲解，课时流程，感悟新知，知识点，菱形的定义及其性质，性质如下表等内容，欢迎下载使用。
菱形的定义及其性质菱形的判定
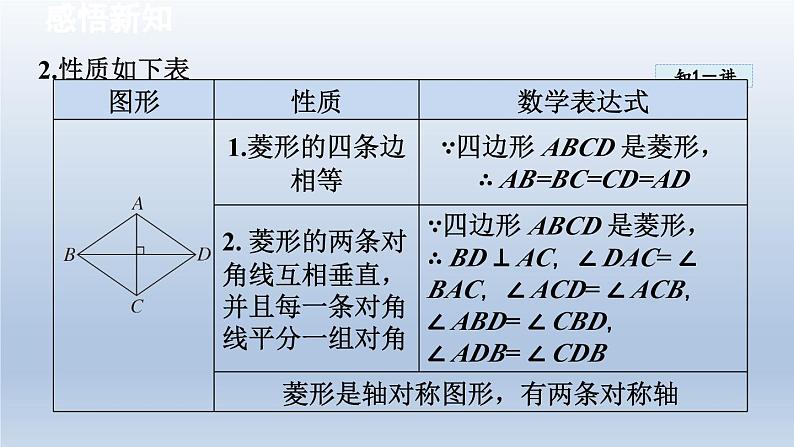
1.定义  有一组邻边相等的平行四边形叫做菱形 .
特别提醒1.菱形必须满足两个条件：一是平行四边形；二是一组邻边相等 .二者必须同时具备，缺一不可 .2.菱形的定义既是菱形的基本性质，又是菱形的基本判定方法 .
特别提醒： (1)菱形的性质可以用来证明线段相等，角相等，直线平行、垂直以及进行相关的计算 .(2)菱形的性质与勾股定理联系，可得对角线与边之间的关系，即边长的平方等于两条对角线长的一半的平方和 .(3)如果菱形的一个内角为 60°，那么菱形的两条边与较短的对角线构成的三角形为等边三角形 .(4)菱形的面积 = 底 × 高 = 两条对角线长的乘积的一半 .
3. 矩形与菱形的区别(1)矩形和菱形都建立在平行四边形的基础上，矩形是附加一直角，而菱形是附加一组邻边相等；(2)矩形的两条对角线把矩形分割成四个面积相等的等腰三角形；而菱形的两条对角线把菱形分割成四个全等的直角三角形；(3)矩形的对称轴是两条过两组对边中点的直线，而菱形的对称轴是两条对角线所在的直线 .
如图 19.3-18，在△ ABC 中， DE ∥ BC， EF ∥ AB，BE 平分∠ ABC，求证：四边形 DBFE 是菱形 .
解题秘方：紧扣定义中的“两个条件”进行判定 .
解法提醒菱形的定义既是菱形的性质，又是菱形的一种判定方法 .在用菱形的定义判定一个四边形是菱形时，先判定这个四边形是平行四边形，再证一组邻边相等 .
解：∵ DE ∥ BC， EF ∥ AB，∴四边形 DBFE 是平行四边形，∵ DE ∥ BC，∴∠ DEB= ∠ EBC，∵ BE 平分∠ ABC，∴∠ EBC= ∠ EBD，∴∠ EBD= ∠ DEB，∴ BD=DE，∴四边形 DBFE 是菱形．
如图 19.3-19，在菱形 ABCD 中， E， F 分别是 BC， CD上的点，且∠ B= ∠ EAF=60°，∠ BAE=18° . 求∠ CEF 的度数 .
解题秘方：紧扣菱形的性质、三角形外角的性质求解 .
解：如图 19.3-19，连接 AC.∵ 四边形 ABCD 是菱形，∠ B=60° ，∴ AB=BC=CD=DA，∠ D= ∠ B=60° .∴△ ABC 和△ ACD 均为等边三角形 .∴ AB=AC，∠ B= ∠ ACF= ∠ BAC=60° .
∵∠ EAF=60°，∴∠ BAC= ∠ EAF，∴△ ABE ≌△ ACF ( ASA ) . ∴ AE=AF.又∵∠ EAF=60°，∴△ EAF 是等边三角形 .∴∠ AEF=60° .∵∠ AEC= ∠ B＋∠ BAE= ∠ AEF＋∠ CEF，∴ 60° ＋18° =60° ＋ ∠ CEF. ∴∠ CEF=18° .
技巧点拨在求有关菱形的角的问题时，由于菱形的每条对角线都把菱形分成两个全等的等腰三角形，因此通常通过连接对角线，把四边形问题转化为特殊三角形问题来解答 .
解题秘方：本题考查菱形的性质、矩形的判定和性质、勾股定理等知识 . 解题的关键是灵活运用所学知识解决问题， 属于中考常考题型．
(1)求证： OE=CD；
(2)若菱形 ABCD 的边长为 6，∠ ABC=60°，求 AE 的长 .
解法提醒(1) 只要证明四边形OCED 是矩形即可；(2) 在 Rt △ ACE 中，利用勾股定理即可解决问题 .
1. 判定定理 1 四边都相等的四边形是菱形 .数学语言： 如图19.3-21，在四边形ABCD 中，∵ AB=BC=CD=DA，∴四边形ABCD 是菱形 .
2.判定定理 2 对角线互相垂直的平行四边形是菱形 .数学语言： 如图 19.3-22，在 ▱ ABCD 中，∵ AC ⊥ BD，∴ ▱ ABCD 是菱形 .
[中考·滨州 ] 如图 19.3-23， 过 ▱ ABCD 的对角线 AC与 BD 的交点 E 作两条互相垂直的直线，分别交边 AB， BC，CD， DA 于点 P， M， Q， N．
解题秘方：本题考查了平行四边形的判定与性质，菱形的判定，全等三角形的判定与性质等知识 . 熟练掌握菱形的判定和平行四边形的判定与性质，证明三角形全等是解题的关键．
(1)求证：△ PBE ≌△ QDE；
证明： ∵四边形 ABCD 是平行四边形，∴ EB=ED， AB ∥ CD， ∴∠ EBP= ∠ EDQ，∵∠ BEP= ∠ DEQ，∴△ PBE ≌△ QDE(ASA) .
(2) 顺次连接点P， M， Q， N，求证：四边形 PMQN是菱形．
证明：由(1)得△ PBE ≌△ QDE，∴ EP=EQ，同理可得△ BME ≌△ DNE(ASA)，∴ EM=EN，∴四边形 PMQN 是平行四边形，又∵ PQ ⊥ MN，∴平行四边形 PMQN 是菱形．
方法点拨证明一个四边形是菱形的方法：若已知要证的四边形的对角线互相垂直，则要考虑证明这个四边形是平行四边形，用“对角线互相垂直的平行四边形是菱形”进行证明 .
如图 19.3-24， 在四边形 ABCD 中， AB=CD， 点E， F， G， H 分别是 AD， BD， BC， AC 的中点 . 求证：四边形 EFGH 是菱形 .
解题秘方：紧扣题中中点与线段相等这两个条件， 从证四边相等入手判定菱形 .
技巧点拨判定菱形的方法：1. 若用对角线进行判定：先证明四边形是平行四边形，再证明对角线互相垂直，或直接证明四边形的对角线互相垂直平分；2. 若用边进行判定：先证明四边形是平行四边形，再证明一组邻边相等，或直接证明四边形的四条边都相等 .