2022-2023学年辽宁省沈阳市铁西区九年级上学期数学期末试题及答案

这是一份2022-2023学年辽宁省沈阳市铁西区九年级上学期数学期末试题及答案，共27页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

1. 若，则xy的值为（ ）
A. 12B. C. D. 7
【答案】A
【解析】
【分析】直接根据比例式进行变形即可得到答案．
【详解】解：∵，
∴，
故选：A
【点睛】本题主要考查了比例变形，熟记“内项积等于外项积”是解答本题的关键．
2. 如图所示几何体是由一个球体和一个圆柱组成的，它的俯视图是（ ）
D.
【答案】C
【解析】
【分析】根据俯视图的意义和画法可以得出答案．
【详解】根据俯视图的意义可知，从上面看物体所得到的图形，选项C符合题意，
故答案选：C．
【点睛】本题主要考查组合体的三视图，注意虚线、实线的区别，掌握俯视图是从物体的上面看得到的视图是解题的关键．
3. 已知关于的方程的一个根是-1，则的值是（ ）
A. -2B. -1C. 1D. 2
【答案】D
【解析】
【分析】把代入方程得，然后解关于的方程．
【详解】解：把代入方程，得：，
解得：．
故选：D．
【点睛】本题考查一元二次方程的解，熟知方程的解即为能使方程两边相等的未知数的值是解题关键．
4. 小红有两顶帽子，分别为粉色和黑色，有两条围巾，分别为粉色和白色，她随机拿出一顶帽子和一条围巾戴上，恰好为粉色帽子和粉色围巾的概率是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据题意画出树状图，用符合要求的情况数除以所有等可能情况数即可．
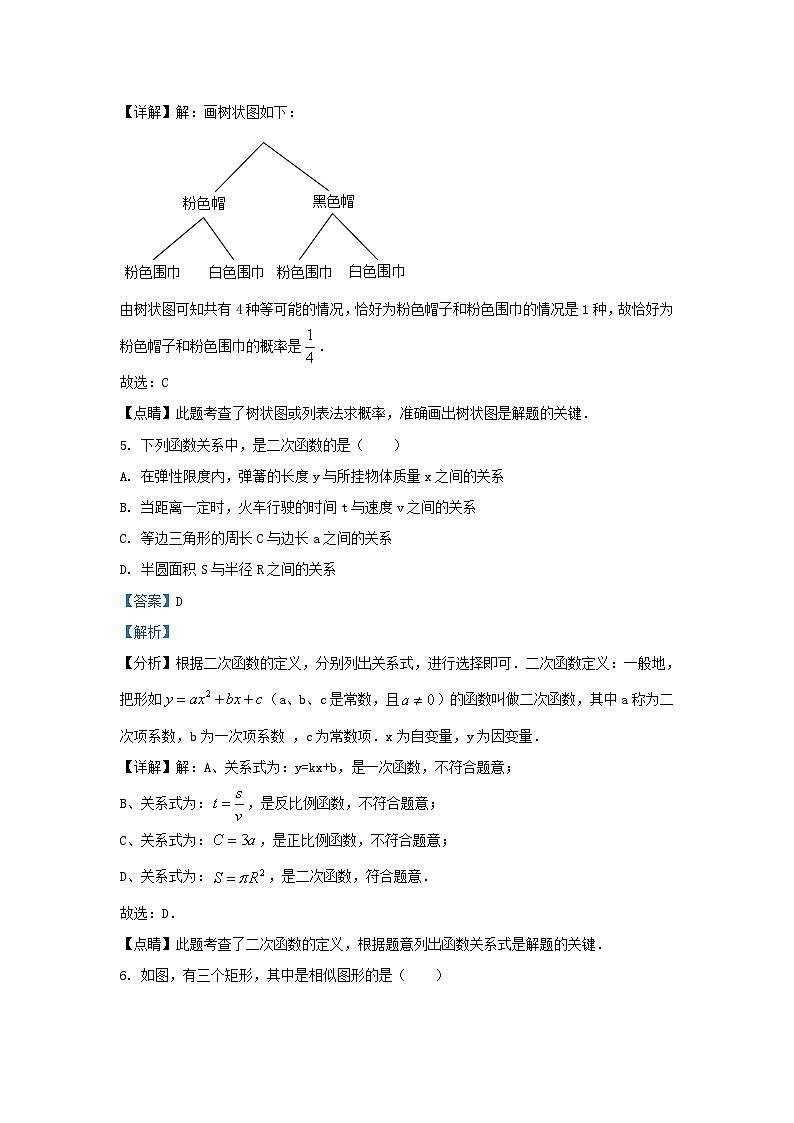
【详解】解：画树状图如下：
由树状图可知共有4种等可能的情况，恰好为粉色帽子和粉色围巾的情况是1种，故恰好为粉色帽子和粉色围巾的概率是．
故选：C
【点睛】此题考查了树状图或列表法求概率，准确画出树状图是解题的关键．
5. 下列函数关系中，是二次函数的是（ ）
A. 在弹性限度内，弹簧的长度y与所挂物体质量x之间的关系
B. 当距离一定时，火车行驶的时间t与速度v之间的关系
C. 等边三角形的周长C与边长a之间的关系
D. 半圆面积S与半径R之间的关系
【答案】D
【解析】
【分析】根据二次函数的定义，分别列出关系式，进行选择即可．二次函数定义：一般地，把形如（a、b、c是常数，且）的函数叫做二次函数，其中a称为二次项系数，b为一次项系数 ，c为常数项．x为自变量，y为因变量．
【详解】解：A、关系式为：y=kx+b，一次函数，不符合题意；
B、关系式为：，是反比例函数，不符合题意；
C、关系式为：，是正比例函数，不符合题意；
D、关系式为：，是二次函数，符合题意．
故选：D．
【点睛】此题考查了二次函数的定义，根据题意列出函数关系式是解题的关键．
6. 如图，有三个矩形，其中是相似图形的是（ ）
A. 甲和乙B. 甲和丙C. 乙和丙D. 甲、乙和丙
【答案】B
【解析】
【分析】根据对应角相等且对应边成比例的两个多边形相似即可判断．
【详解】解：∵，
∴是相似形的是甲和丙
故选B．
【点睛】本题主要考查了相似多边形的判定，熟知相似多边形对应边成比例是解题的关键．
7. 已知反比例函数，当时，y的最大值是6，则当时，y有（ ）
A. 最小值B. 最小值C. 最大值D. 最大值
【答案】B
【解析】
【分析】由函数经过第二象限，可确定，则在上，y值随x值的增大而增大，即可确定函数的解析式为，由此可求解．
【详解】解：∵当时，y的最大值是6，
∴反比例函数经过第二象限，
∴，
∴在上，y值随x值的增大而增大，
∴当时，y有最大值，
∵y的最大值是6，
∴，
∴，
∴，
当时，有最小值，
故选：B．
【点睛】本题考查反比例函数的图象及性质；熟练掌握反比例函数的图象及性质，通过所给条件确定是解题的关键．
8. 下列方程没有实数根的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】通过题目可知这几个方程都是一元二次方程，因此可以通过来确定有没有实数根，即可求解
【详解】解：A、△=，有两个不相等的实数根；
B、△=，故有两个不相等的实数根；
C、△=,故没有实数根；
D、△=，故有两个不相等的实数根
故选C
9. 如图，菱形对角线交点与坐标原点重合，点，则点的坐标为（ ）
B.
C. D.
【答案】B
【解析】
【分析】根据菱形的中心对称性，A、C坐标关于原点对称，利用横反纵也反的口诀求解即可．
【详解】∵菱形是中心对称图形，且对称中心为原点，
∴A、C坐标关于原点对称，
∴C的坐标为，
故选B．
【点睛】本题考查了菱形的中心对称性质，原点对称，熟练掌握菱形的性质，关于原点对称点的坐标特点是解题的关键．
10. 如图，二次函数的图象与y轴的交点在（0，1）与（0，2）之间，对称轴为，函数最大值为4，结合图象给出下列结论：①；②；③；④若关于x的一元二次方程 有两个不相等的实数根，则m>4；⑤当x<0时，y随x的增大而减小．其中正确的结论有（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】
【分析】根据二次函数图象与性质逐个结论进行分析判断即可．
【详解】解：∵二次函数的对称轴为，
∴
∴故①正确；
∵函数图象开口向下，对称轴为，函数最大值为4，
∴函数的顶点坐标为（-1，4）
当x=-1时，
∴
∴，
∵二次函数的图象与y轴的交点在（0，1）与（0，2）之间，
∴<<2
∴<4+a<2
∴，故②正确；
∵抛物线与x轴有两个交点，
∴
∴，故③正确；
∵抛物线的顶点坐标为（-1，4）且方程有两个不相等的实数根，
∴
∴，故④错误；
由图象可得，当x>-1时，y随x增大而减小，故⑤错误．
所以，正确的结论是①②③，共3个，
故选：B
【点睛】本题主要考查了二次函数图象与性质，，熟练掌握二次函数的图象与性质是解答本题的关键．
二、填空题（每小题3分，共18分）
11. 把一元二次方程化成的一般形式，其中，则常数项是___________．
【答案】
【解析】
【分析】直接利用一元二次方程的一般形式分析得出答案．
【详解】解：将一元二次方程化成一般形式之后，
变为，
故常数项是：．
故答案为：．
【点睛】此题主要考查了一元二次方程的一般形式，正确把握定义是解题关键．
12. 从同一批产品中抽检了1000件，其中不合格的产品有10件，由此估计从这批产品中抽检1件产品合格的概率是___________．
【答案】
【解析】
【分析】合格品占总数的百分比即为产品合格的概率．
【详解】解：抽检1件产品合格的概率是．
故答案为：
【点睛】此题考查了概率，熟知用频率估计概率是解题的关键．
13. 如图，和是以点为位似中心的位似图形．若，则与的周长比是_________．
【答案】
【解析】
【分析】根据位似图形性质，得到，根据得到相似比为，再结合三角形的周长比等于相似比即可得到结论．
【详解】解：和是以点为位似中心的位似图形，
，
，
，
，
根据与的周长比等于相似比可得，
故答案为：．
【点睛】本题考查相似图形的性质，掌握位似图形与相似图形的关系，熟记相似图形的性质是解决问题的关键．
14. 如图，小亮从一盏9米高的路灯下处向前走了米到达点处时，发现自己在地面上的影子CE是米，则小亮的身高DC为____________米．
【答案】1.8
【解析】
【分析】同一时刻下物体高度的比等于影长的比，构造相似三角形计算即可．
【详解】如图，由题意知米，米，米，且，
∴米，
∵，
∴
又∵
∴，
∴，即，
解得（米），即小亮的身高为1.8米；
故答案为：1.8.
【点睛】本题考查平行投影相关知识点，能够根据题意构造相似是解题关键点．
15. 已知点P为二次函数图象上一点，设这个二次函数的图象与x轴交于A，B两点（A在B的右侧），与y轴交于C点，若，则点P的横坐标的值为___________．
【答案】
【解析】
【分析】先求出点，，证明是等腰直角三角形，则，由得到，设直线与y轴交点为点D ,可证是等腰直角三角形，，得到D的坐标是，用待定系数法求出直线的解析式为，直线的解析式与二次函数联立，解方程组即可得到点P的横坐标的值．
【详解】解：当时，，解得，
由题意可知，，
当时，，
∴，
如图所示，
∵，，
∴是等腰直角三角形，
∴，
∵，
∴，
设直线与y轴的交点为点D ,
∵，
∴是等腰直角三角形，
∴，
∴点D的坐标是，
设直线的解析式为，把代入得，
，解得，
∴直线的解析式为，
联立得，，
解得或,
即点P的坐标是，
∴点P的横坐标的值为．
故答案为：
【点睛】此题是二次函数综合题，考查了等腰直角三角形的判定和性质、待定系数法求一次函数解析式、函数图象的交点问题等知识，数形结合和准确计算是解题的关键．
16. 正方形中，，点E在直线上，且，连接，线段的垂直平分线交边于点F，则的长为___________．
【答案】或
【解析】
【分析】分点E在线段上时，点E在线段的延长线上时，点E在线段的延长线上时三种情况求解即可．
【详解】当点E在线段上时，如图1，连接．

∵正方形中，，
∴，．
∵，
∴．
设，则．
∵线段的垂直平分线交边于点F，
∴．
∴，
∴，
解得．
点E在线段的延长线上时，如图2，连接．
∵正方形中，，
∴，．
∵，
∴．
设，则．
∵线段的垂直平分线交边于点F，
∴．
∴，
∴，
解得．
点E在线段的延长线上时，如图3，此时线段的垂直平分线与边无交点，不符合题意．
综上可知，的长为或．
故答案为：或．
【点睛】本题考查了正方形的性质，线段垂直平分线的性质，勾股定理等知识，分类讨论是解答本题的关键．
三、（17题6分，18题、19题各8分，共22分）
17. 解方程：．
【答案】，
【解析】
【分析】利用公式法求解即可．
【详解】，
，，，
，
，，
即：，．
【点睛】本题主要考查解一元二次方程，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
18. 已知矩形的对角线，相交于点O，点E是边上一点，连接，，，且．求证：．
【答案】见解析
【解析】
【分析】由矩形的性质得到，再利用即可判定．
【详解】证明：∵四边形是矩形，
∴，
在和中，
，
∴．
【点睛】此题考查了矩形的性质和全等三角形的判定，利用矩形的性质得到是解题的关键．
19. 张老师和王老师参加了学校组织的党员志愿者活动，积极参与学校的常规服务．每个志愿者都可以从以下三个项目中任选一项参加：①早晨组织学生按秩序入校；②组织学生午餐；③带领学生进行体育锻炼．请用列表或画树状图的方法，求张老师和王老师选择参加同一项目的概率（用序号表示各项目）．
【答案】张老师和王老师选择参加同一项目的概率为．
【解析】
【分析】根据题意列表法求概率即可求解．
【详解】解：依题意，列表如下，
共有9种等可能结果，其中张老师和王老师选择参加同一项目的有3种，
∴张老师和王老师选择参加同一项目的概率为．
【点睛】本题考查了列表法求概率，掌握列表法是解题的关键．
四、（20题、21题各8分，共16分）
20. 某果园有棵橙子树，平均每棵树结个橙子．现准备多种一些橙子树以提高果园产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结个橙子．假设果园增种棵橙子树，增种后果园橙子的总产量为个，那么请你求出当果园增种多少棵橙子树时，橙子的总产量最多，并求出此时的总产量．
【答案】当果园增种棵橙子树时，橙子的总产量最多，此时的总产量为个
【解析】
【分析】平均每棵树结个橙子，假设果园增种棵橙子树，假设果园增种棵橙子树，平均每棵树结个橙子，可知现在有棵树，平均每颗产量为，由此即可求解．
【详解】解：有棵橙子树，平均每棵树结个橙子，假设果园增种棵橙子树，假设果园增种棵橙子树，增种后果园橙子的总产量为个，
∴，
∴当时，总产量为有最大值，其最大值为，
∴当果园增种棵橙子树时，橙子的总产量最多，此时的总产量为个．
【点睛】本题主要考查二次函数与实际问题的综合，分析题目意思，找出数量关系，列方程，掌握二次函数图像的性质特征是解题的关键．
21. 如图，在中，，点D在边上，作交边于点E，，．将绕点C旋转，旋转后点D的对应点为点F，点E的对应点为点G，且点F在的内部，连接．
（1）求的值；
（2）判断直线与的位置关系，并说明理由．
【答案】（1）；
（2），理由见解析．
【解析】
【分析】（1）证明，则，由旋转的性质得到，，则，则，即可得到答案；
（2）延长交于点H，由，得，由得到，进一步得到，即可得到结论．
【小问1详解】
解：∵，
∴
∴，
∴，
∵绕点C旋转，旋转后点D的对应点为点F，点E的对应点为点G，
∴，，
∴，
∴，
∴；
【小问2详解】
，理由如下：
延长交于点H，
∵，
∴，
∵，
∴，
∴，
∴，
∴，
即．
【点睛】此题考查了相似三角形的判定和性质、图形的旋转等知识，熟练掌握相似三角形的判定和性质是解题的关键．
22. 某厂家今年一月份的口罩产量是万个，三月份的口罩产量是万个，求该厂家一月份到三月份的口罩产量的月平均增长率．
【答案】该厂家一月份到三月份的口罩产量的月平均增长率为．
【解析】
【分析】设该厂家一月份到三月份的口罩产量的月平均增长率为x，根据一月份的口罩产量是万个，三月份的口罩产量是万个，列出方程，解方程即可得到答案．
【详解】解：设该厂家一月份到三月份的口罩产量的月平均增长率为x，
由题意得，
解得，（不合题意，舍去）
∴该厂家一月份到三月份的口罩产量的月平均增长率为．
【点睛】此题考查了一元二次方程的应用，读懂题意，准确列出方程是解题的关键．
23. 如图，在平面直角坐标系中，等腰直角三角形的直角顶点B的坐标为，点A在y轴正半轴上，将沿y轴向下平移得到，点B的对应点E恰好在反比例函数的图象上．
（1）求m的值；
（2）求平移的距离；
（3）点P是x轴上的一个动点，当的周长最小时，请直接写出此时点P的坐标及的周长．
【答案】（1）；
（2）5个单位长度； （3），
【解析】
【分析】（1）过点作轴，易得为等腰直角三角形，即可得解；
（2）根据平移规则，点横坐标为，设，根据点E在反比例函数的图象上，求出的值，即可得解；
（3）的周长，为定长，则当的值最小时，的周长最小，作点关于轴的对称点，，当且仅当三点共线时，的值最小，连接，与轴的交点即为点，求出的解析式，进而求出点坐标，即可得解．
【小问1详解】
解：过点作轴于点，
∵是等腰直角三角形，
∴，
∴，
∴为等腰直角三角形，
∴，
∵点B的坐标为，
∴，即：；
【小问2详解】
解：将沿y轴向下平移得到，点B的对应点为E，
∴点横坐标为，设，
∵点E在反比例函数的图象上，
∴，
∴，
∴；
∴平移的距离为：；
【小问3详解】
解：∵的周长，为定长，
∴当的值最小时，的周长最小，
作点关于轴的对称点，，当且仅当三点共线时，的值最小，连接，与轴的交点即为点，如图，
则：，根据平移规则，可得：，
设直线的解析式为：，
则：，解得：，
∴，
当时，，
∴，
∵，，，
∴，
∴的周长．
【点睛】本题考查坐标与图形，以及坐标系下的平移，轴对称，同时考查了反比例函数图象上的点的特征，以及一次函数与坐标轴的交点．本题的综合性较强，熟练掌握相关知识点，利用数形结合的思想进行求解，是解题的关键．
24. （1）如图1，中，点D在边上，且与点B，C不重合，点G是线段上一点，不与点A，D重合，过点G作，分别交于点E，F．
①求证：；
②连接，当四边形是平行四边形时，___________；
（2）如图2，在中，是中线，点E在线段上，交于点F，，且点G与点E在边两侧，连接，，，，，请直接写出的长．
【答案】（1）①见解析；②；（2）．
【解析】
【分析】（1）①证明，利用相似三角形的性质即可证明绪论
②证明，和，据此即可求解；
（2）延长交于点H，连接交于点N，利用相似三角形的判定和性质推出是线段的垂直平分线，，，，证明，利用勾股定理即可求解．
【详解】解：（1）①证明：∵，
∴，
∴，，
∴；
②∵四边形是平行四边形，且，
∴，，，
∴，，
∴，
同理可证，
∵四边形是平行四边形，
∴，
∴，
故答案为：；
（2）延长交于点H，连接交于点N，交于点M，
∵，
∴，，
∴，，
∵是中线，即，
∴，
∵，即是线段的垂直平分线，
∴，，
∵，，
∴，则，，
∵，，
∴，即，
∵，
∴，而，
∴，
∴．
【点睛】本题考查了相似三角形的判定和性质，线段垂直平分线的判定和性质，勾股定理，证明是线段的垂直平分线，是解题的关键．
25. 如图抛物线的对称轴为，对称轴与轴交于点，抛物线与轴交于点，点为抛物线上的两个动点，且点在点的右侧，．
（1）求该抛物线的函数表达式及线段的长；
（2）当点与点重合时，直接写出点的坐标；
（3）当点不与点重合时，且与（2）中的相似时，请直接写出点的横坐标．
【答案】（1），；
（2）；
（3），
【解析】
【分析】（1）根据对称轴的计算公式，可求出二次函数的系数，由此即可求解；
（2）如图所示，点与点重合，过点作轴于，根据三角形的相似，三角函数即可求解；
（3）如图所示，在中，，分别过点，作轴于，作轴于，可得，根据边的关系列方程即可求解．
小问1详解】
解：抛物线的对称轴为，
∴，
∴，
∴该抛物线的函数表达式，
令，则，
∴点的坐标为，即；
∵对称轴与轴交于点，
∴，
∴．
【小问2详解】
解：如图所示，点与点重合，过点作轴于，
∵，
∴，且，
∴，
∴，
设，则，
∴，
∴点的坐标为，且点在抛物线上，
∴把点的坐标为代入二次函数解析式得，，整理得，，解得，，，
∵，
∴，
∴点的坐标为，
∴点与点重合时，点的坐标为．
【小问3详解】
解：由（2）可知，，
∴，
∴是等腰直角三角形，则也是等腰直角三角形，如图所示，在中，，分别过点，作轴于，作轴于，
∵点在抛物线上，
∴设，，则点，，
∴，，，，
∵，
∴，且，
∴，且，
在和中，
，
∴，
∴，，
∴，即，整理得，，
∴，
，则，
，则，
∴，，
∴当时，代入得，，解得，，，
∴当时，，则，
∴点的坐标为；
当时，，则，
∴点的坐标为，即点与点重合，
∵点在点的右侧，点不与点重合，
∴时，不符合题意，故舍去；
当时，代入得，，解得，，，
∴当，则，与题目中“点在点的右侧”不符，舍去；
当，则，
∴，
∴点的坐标为，
综上所述，点的横坐标为，．
【点睛】本题主要考查二次函数动点与几何图形的综合，理解图示中动点的运动规律，二次函数图像的性质，几何图形的性质是解题的关键．王老师
张老师
①
②
③
①
①①
①②
①③
②
②①
②②
②③
③
③①
③②
③③