2024九年级数学下册第29章直线与圆的位置关系集训课堂练素养1.用三角函数解圆中的计算问题习题课件新版冀教版

这是一份2024九年级数学下册第29章直线与圆的位置关系集训课堂练素养1.用三角函数解圆中的计算问题习题课件新版冀教版，共36页。

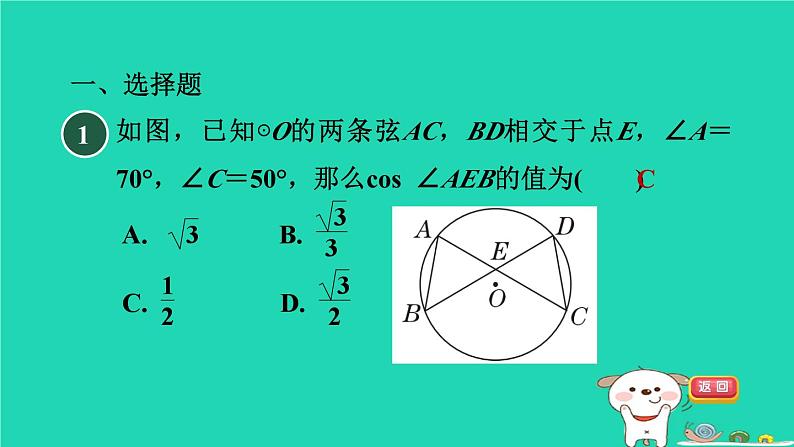
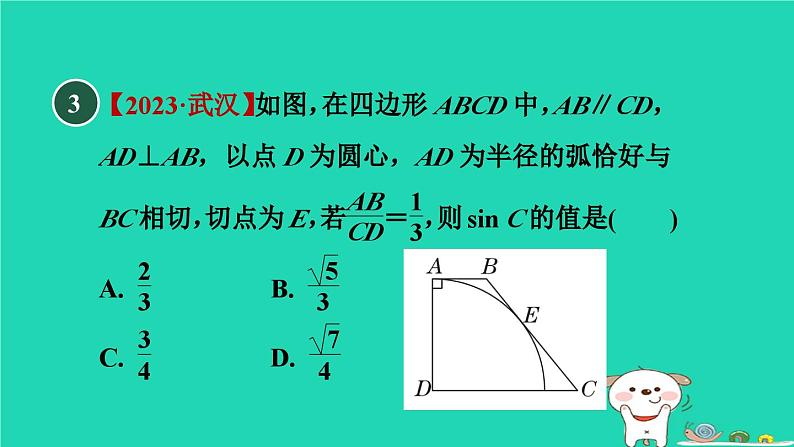
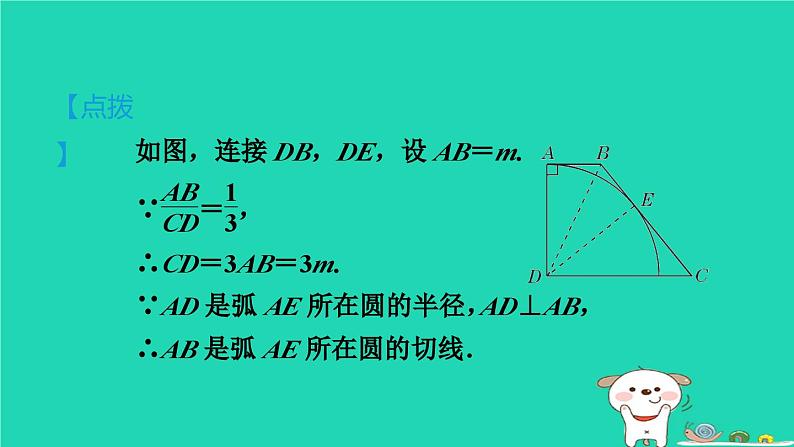
冀教版 九年级下第二十九章 直线与圆的位置关系练素养　1.用三角函数解圆中的计算问题集训课堂 如图，已知⊙O的两条弦AC，BD相交于点E，∠A＝70°，∠C＝50°，那么cos ∠AEB的值为(　　)C1一、选择题2【母题：教材P21复习题A组T6】如图所示，⊙M与x轴相交于A(2，0)，B(8，0)，与y轴相切于点C，P是ACB上的一点，则tan ∠APB等于(　　)︵【点拨】如图所示，作MN⊥AB于点N，连接MA，MB，MC. 则∠AMN＝∠BMN，AN＝BN.∵A(2，0)，B(8，0)，∴OA＝2，OB＝8，AN＝BN＝3.∵C是⊙M与y轴的切点，∴∠MCO＝∠CON＝∠MNO＝90°.【答案】 B3【点拨】【答案】 B4【2022·杭州】如图，已知△ABC内接于半径为1的⊙O，∠BAC＝θ(θ是锐角)，则△ABC的面积的最大值为(　　)A．cos θ(1＋cos θ) B．cos θ(1＋sin θ)C．sin θ(1＋sin θ) D．sin θ(1＋cos θ)【点拨】当△ABC的高经过圆心时，即点A与点A′重合，△ABC的面积最大，连接OB，如图所示．∵A′D⊥BC，∴BC＝2BD，∠BOD＝∠BA′C＝θ.【答案】 D5如图，在半径为5的⊙O中，弦AB＝6，点C是优弧AB上的一点(不与A，B重合)，则cos C的值为________．二、填空题6【点拨】如图，连接OD.∵AB是⊙O的直径，且经过弦CD的中点H，∴AB⊥CD.∴∠OHD＝∠BHD＝90°.7【新考法•等角代换法】如图，在直角坐标系中，四边形OABC是直角梯形，BC∥OA，⊙P分别与OA，OC，BC相切于点E，D，B，与AB交于点F，已知A(2，0)，B(1，2)，则tan ∠FDE＝________.【点拨】连接PB，PE，易知点B，P，E在一条直线上，进而得出BE是⊙P的直径．因为∠ABE＝∠FDE，所以求出tan∠ABE即可．8【2023·衡阳】如图，AB是⊙O的直径，AC是一条弦，点D是弧AC的中点，DE⊥AB于点E，交AC于点F，交⊙O于点H，DB交AC于点G.三、解答题证明：∵点D是弧AC的中点，∴AD＝CD.∵AB⊥DH，且AB是⊙O的直径，∴AD＝AH，∴CD＝AH.∴∠ADH＝∠CAD.∴AF＝DF.(1)求证：AF＝DF；︵︵︵︵︵︵9【2022•南充】【新考法•构造直角三角形法】如图，AB为⊙O的直径，点C是⊙O上一点，点D是⊙O外一点，∠BCD＝∠BAC，连接OD交BC于点E.证明：如图，连接OC.∵AB是⊙O的直径，∴∠ACB＝90°.∴∠A＋∠B＝90°. ∵OC＝OB，∴∠OCB＝∠B.∵∠BCD＝∠A，∴∠OCB＋∠DCB＝90°.∴OC⊥CD. ∵OC为⊙O的半径，∴CD是⊙O的切线．(1)求证：CD是⊙O的切线；10【2023•广元】【新考法•函数比法】如图，AB为⊙O的直径，点C为⊙O上一点，连接AC，BC，过点C作⊙O的切线交AB的延长线于点D，OF⊥BC于点E，交CD于点F.证明：如图，连接OC.∵CD是⊙O的切线，∴∠OCD＝90°，∴∠OCB＋∠BCD＝90°.∵OF⊥BC，∴∠BEO＝90°，∴∠BOE＋∠OBE＝90°.∵OC＝OB，∴∠OCB＝∠OBC，∴∠BCD＝∠BOE.(1)求证：∠BCD＝∠BOE；11【2022·娄底】如图，已知BD是Rt△ABC的角平分线，点O是斜边AB上的动点，以点O为圆心，OB长为半径的⊙O经过点D，与OA相交于点E.解：AC与⊙O相切．理由如下：如图，连接OD. ∵OD＝OB，∴∠ODB＝∠OBD.∵BD是Rt△ABC的角平分线，∴∠OBD＝∠DBC.∴∠ODB＝∠DBC.∴OD∥BC.∴∠ODA＝∠C＝90°，即AC⊥OD.∵OD是⊙O的半径，∴AC是⊙O的切线，即AC与⊙O相切．(1)判定AC与⊙O的位置关系，并说明理由．②试用sin∠DBC和cos∠DBC表示sin∠ABC，猜测sin 2α与sinα，cosα的关系，并用α＝30°给予验证．