



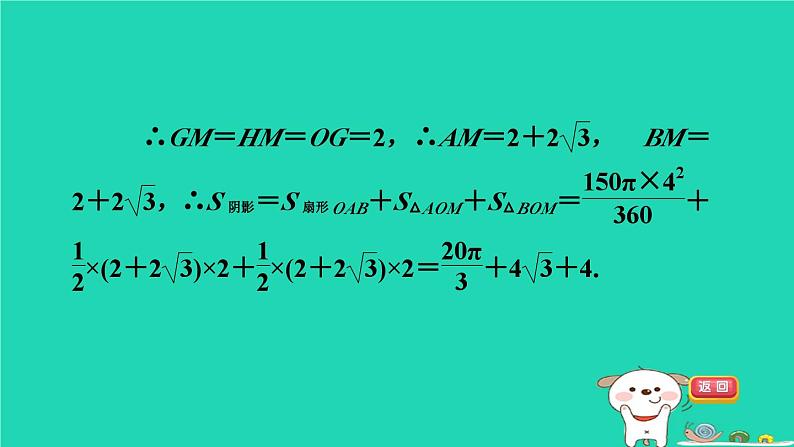
还剩16页未读,
继续阅读
2024九年级数学下册第29章直线与圆的位置关系集训课堂练素养3.不规则图形面积的求法习题课件新版冀教版
展开
这是一份2024九年级数学下册第29章直线与圆的位置关系集训课堂练素养3.不规则图形面积的求法习题课件新版冀教版,共24页。
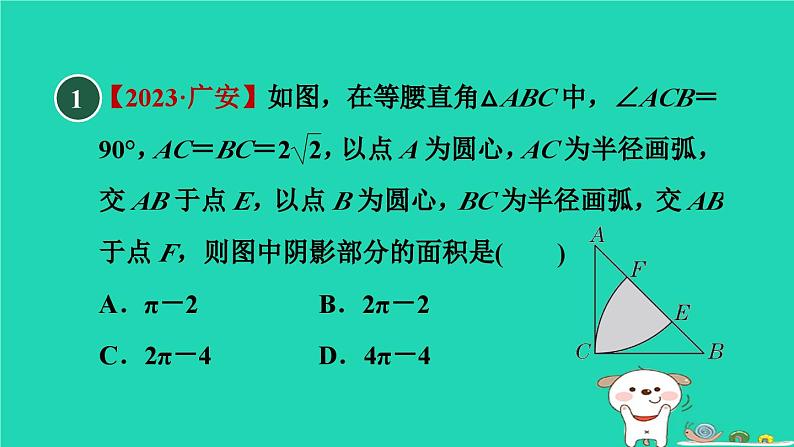
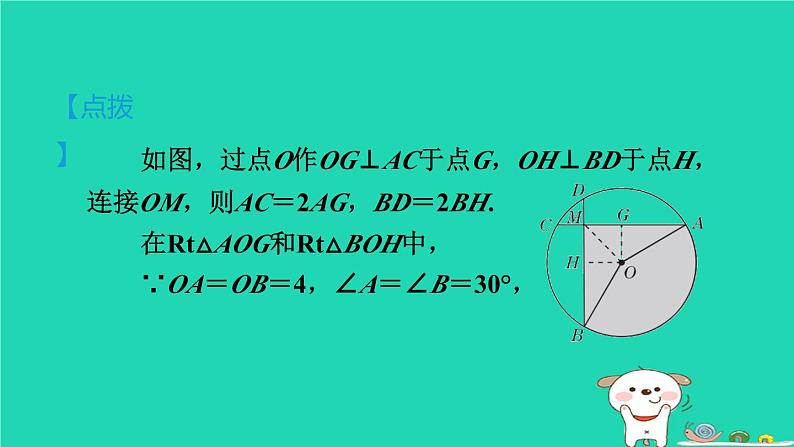
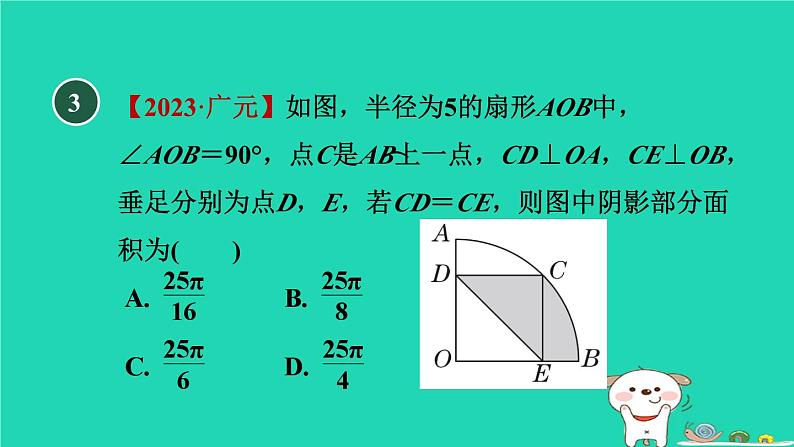
冀教版 九年级下第二十九章 直线与圆的位置关系练素养 3.不规则图形面积的求法集训课堂 1【答案】 C【点拨】2如图,在⊙O中,弦AC,BD相交于点M,AC⊥BD,连接OA,OB,∠A=∠B=30°,OA=4,则图中阴影部分的面积为______________.【点拨】如图,过点O作OG⊥AC于点G,OH⊥BD于点H,连接OM,则AC=2AG,BD=2BH.在Rt△AOG和Rt△BOH中,∵OA=OB=4,∠A=∠B=30°,3【2023·广元】如图,半径为5的扇形AOB中,∠AOB=90°,点C是AB上一点,CD⊥OA,CE⊥OB,垂足分别为点D,E,若CD=CE,则图中阴影部分面积为( )︵【点拨】连接OC,如图所示.∵CD⊥OA,CE⊥OB,∴∠ODC=∠OEC=90°.∵∠AOB=90°,∴四边形OECD是矩形.【答案】 B4如图,AB是⊙O的直径,CD是⊙O的弦,且CD∥AB,AB=12,CD=6,则图中阴影部分的面积为( )A.18π B.12πC.6π D.3π【答案】 C【点拨】5如图,AB是⊙O的直径,⊙O的弦DC的延长线与AB的延长线相交于点P,OD⊥AC于点E,∠CAB=15°,OA=2,则阴影部分的面积为( )【答案】 B【点拨】6【点拨】如图,连接CD.∵BC是半圆的直径,∴∠CDB=90°,即CD⊥AB.∵在Rt△ABC中,∠ACB=90°,【答案】 D7如图,将半径为2,圆心角为120°的扇形OAB绕点B逆时针旋转60°,得到扇形O′A′B,其中点A的运动路径为AA′,则图中阴影部分的面积为____________.︵【点拨】如图,连接AB,A′B,AO′,OO′.OO′与AB交于点C.∵将半径为2,圆心角为120°的扇形OAB绕点B逆时针旋转60°得到扇形O′A′B,∴∠ABA′=60°,∠OBO′=60°,OB=O′B,8如图,正方形ABCD的边AB=1,BD和AC都是以1为半径的圆弧,两阴影部分的面积分别记为S1和S2,则S1-S2等于( )︵︵【点拨】如图,正方形ABCD的面积为S1+S2+S3+S4,① 扇形DAB和扇形ADC的面积和为2S1+S3+S4. ② 【答案】 A
冀教版 九年级下第二十九章 直线与圆的位置关系练素养 3.不规则图形面积的求法集训课堂 1【答案】 C【点拨】2如图,在⊙O中,弦AC,BD相交于点M,AC⊥BD,连接OA,OB,∠A=∠B=30°,OA=4,则图中阴影部分的面积为______________.【点拨】如图,过点O作OG⊥AC于点G,OH⊥BD于点H,连接OM,则AC=2AG,BD=2BH.在Rt△AOG和Rt△BOH中,∵OA=OB=4,∠A=∠B=30°,3【2023·广元】如图,半径为5的扇形AOB中,∠AOB=90°,点C是AB上一点,CD⊥OA,CE⊥OB,垂足分别为点D,E,若CD=CE,则图中阴影部分面积为( )︵【点拨】连接OC,如图所示.∵CD⊥OA,CE⊥OB,∴∠ODC=∠OEC=90°.∵∠AOB=90°,∴四边形OECD是矩形.【答案】 B4如图,AB是⊙O的直径,CD是⊙O的弦,且CD∥AB,AB=12,CD=6,则图中阴影部分的面积为( )A.18π B.12πC.6π D.3π【答案】 C【点拨】5如图,AB是⊙O的直径,⊙O的弦DC的延长线与AB的延长线相交于点P,OD⊥AC于点E,∠CAB=15°,OA=2,则阴影部分的面积为( )【答案】 B【点拨】6【点拨】如图,连接CD.∵BC是半圆的直径,∴∠CDB=90°,即CD⊥AB.∵在Rt△ABC中,∠ACB=90°,【答案】 D7如图,将半径为2,圆心角为120°的扇形OAB绕点B逆时针旋转60°,得到扇形O′A′B,其中点A的运动路径为AA′,则图中阴影部分的面积为____________.︵【点拨】如图,连接AB,A′B,AO′,OO′.OO′与AB交于点C.∵将半径为2,圆心角为120°的扇形OAB绕点B逆时针旋转60°得到扇形O′A′B,∴∠ABA′=60°,∠OBO′=60°,OB=O′B,8如图,正方形ABCD的边AB=1,BD和AC都是以1为半径的圆弧,两阴影部分的面积分别记为S1和S2,则S1-S2等于( )︵︵【点拨】如图,正方形ABCD的面积为S1+S2+S3+S4,① 扇形DAB和扇形ADC的面积和为2S1+S3+S4. ② 【答案】 A
相关资料
更多









