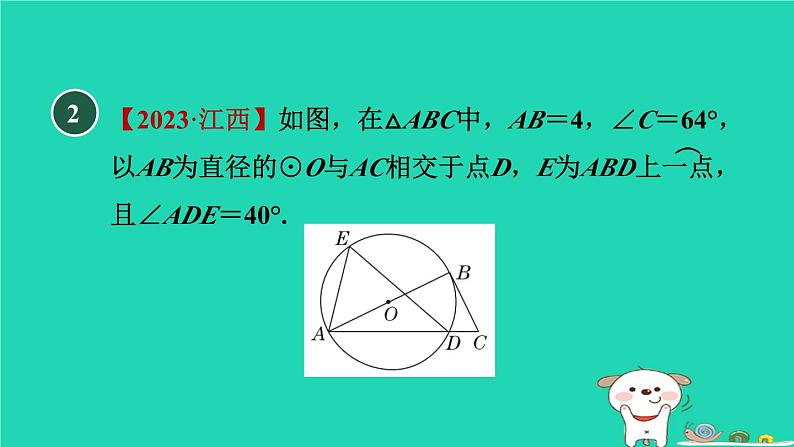
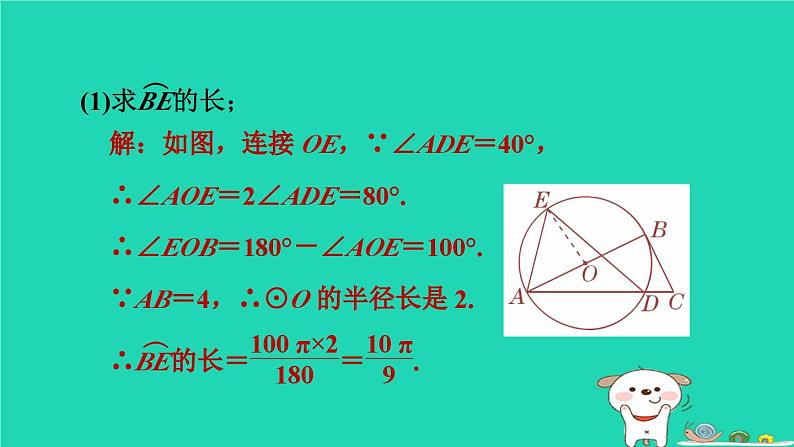
2024九年级数学下册第29章直线与圆的位置关系全章热门考点整合应用习题课件新版冀教版

这是一份2024九年级数学下册第29章直线与圆的位置关系全章热门考点整合应用习题课件新版冀教版，共30页。

冀教版 九年级下第二十九章 直线与圆的位置关系全章热门考点整合应用【新考法·方程思想法】由于过度采伐森林和破坏植被，我国某些地区多次受到沙尘暴的侵袭．近来A市气象局测得沙尘暴中心在A市正东方向400 km的B处，正向西北方向转移，如图所示，距沙尘暴中心300 km的范围内将受到影响，则A市是否会受到这次沙尘暴的影响？1解：如图，过点A作AC⊥BD于点C.由题意，得AB＝400 km，∠DBA＝45°，易知AC＝BC.在Rt△ABC中，设AC＝BC＝x km.由勾股定理，得AC2＋BC2＝AB2，2【2023·江西】如图，在△ABC中，AB＝4，∠C＝64°，以AB为直径的⊙O与AC相交于点D，E为ABD上一点，且∠ADE＝40°.︵(1)求BE的长；︵︵(2)若∠EAD＝76°，求证：CB为⊙O的切线．3如图，已知⊙O的内接正十边形ABCD…，AD分别交OB，OC于M，N.求证：证明：如图，连接OA，OD，则∠AOB＝∠BOC＝∠COD＝360°÷10＝36°，∴∠AOD＝∠AOB＋∠BOC＋∠COD＝108°.又∵OA＝OD，∴∠OAD＝∠ODA＝36°.(1) MN∥BC；∴∠ANO＝∠COD＋∠ODA＝36°＋36°＝72°.∵∠BOC＝36°，OB＝OC，∴∠BCO＝∠OBC＝72°.∴∠ANO＝∠BCO.∴MN∥BC.(2)MN＋BC＝OB.4【2023·无锡天一实验学校二模】如图，P为⊙O外一点，PA，PB是⊙O的切线，A，B为切点，点C在⊙O上，连接OA，OC，AC.证明：如图，过O作OH⊥AC于H，则∠OHA＝90°.∴∠AOH＋∠OAC＝90°.∵PA是⊙O的切线，∴∠OAP＝90°.∴∠OAC＋∠PAC＝90°.∴∠AOH＝∠PAC.∵OA＝OC，OH⊥AC，∴∠AOC＝2∠AOH.∴∠AOC＝2∠PAC.(1)求证：∠AOC＝2∠PAC；解：如图，延长AC交PB于E，∵PA，PB是⊙O的切线，∴OB⊥PB，PA＝PB.∵AC∥OB，∴AC⊥PB，又∵OH⊥AC，∴四边形OBEH是矩形，∴OH＝BE，HE＝OB＝5.(2)连接OB，若AC∥OB，⊙O的半径为5，AC＝6，求AP的长．5【母题：教材P13练习T1】如图，若△ABC的三边长分别为AB＝9，BC＝5，CA＝6，△ABC的内切圆⊙O分别切AB，BC，AC于点D，E，F，则AF的长为(　　)A．5　　　　　B．10C．7.5 D．4【答案】 A【点拨】C6如图，△ABC的内切圆⊙O与AB，BC，AC分别相切于点D，E，F，连接OE，OF，∠C＝90°，AC＝6，BC＝8，则阴影部分的面积为(　　)7【2023·孝感三模】如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D在AB边上，点E是BC边上一点(不与点B，C重合)，且DA＝DE，则AD的取值范围是________．8证明：连接OC.∵CF是⊙O的切线，点C是切点，∴OC⊥CF，即∠OCF＝90°.∴∠OCB＋∠BCF＝90°.∵CD⊥AB，∴∠BEC＝90°.∴∠BCE＋∠OBC＝90°.∵OB＝OC，∴∠OCB＝∠OBC.∴∠BCE＝∠BCF，即CB平分∠DCF.(1)求证：CB平分∠DCF； (2)G为AD上一点，连接CG交AB于点H，若CH＝3GH，求BH的长．︵9AB是⊙O的直径，C为圆周上一点，BD切⊙O于点B.(1)在图①中，∠BAC＝30°，求∠DBC的度数；解：∵AB是直径，∴∠BCA＝90°，∴∠BAC＋∠ABC＝90°.∵BD切⊙O于点B，∴∠ABD＝90°.∴∠DBC＋∠ABC＝90°，∴∠DBC＝∠BAC＝30°.解：连接AC，则∠CAB＝∠CA1B，由(1)知∠DBC＝∠BAC，∴∠BA1C＝∠DBC，∵∠BA1C＝50°，∴∠DBC＝50°.(2)在图②中，∠BA1C＝50°，求∠DBC的度数；解：连接AC，同(2)可证∠BA1C＝∠DBC，∵∠BA1C＝α，∴∠DBC＝α.(3)在图③中，∠BA1C＝α，求∠DBC的度数；解：过圆上一点作圆的一条切线和一条弦，则这条弦和切线相交所形成的角等于它们所夹的弧所对的圆周角． (4)通过(1)(2)(3)的探索你发现了什么？用你自己的语言叙述你的发现．【点方法】本题用到转化思想和从特殊到一般的思想，(2)中通过连接AC，把问题转化为(1)，通过(1)(2)中特殊角的推导，得到第(3)问一般的结论．