2024九年级数学下册第30章二次函数30.4二次函数的应用3用二次函数解几何图形中的最值习题课件新版冀教版

这是一份2024九年级数学下册第30章二次函数30.4二次函数的应用3用二次函数解几何图形中的最值习题课件新版冀教版，共34页。
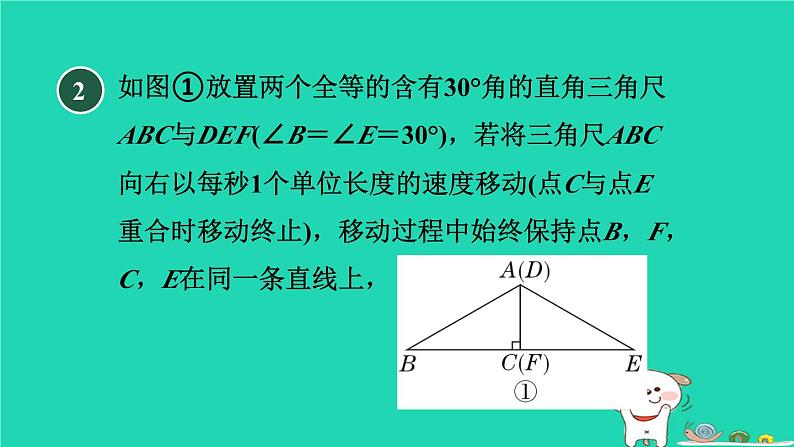
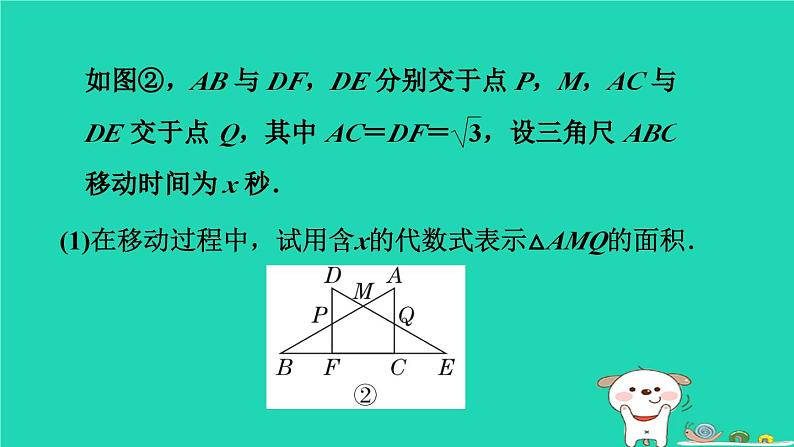
冀教版 九年级下第三十章 二次函数二次函数的应用用二次函数解几何图形中的最值30.4.3 【新考法·化动为定法】如图，在△ABC中，BC＝7 cm，AC＝24 cm，AB＝25 cm，P点在BC上从B点运动到C点，速度为2 cm/s；Q点在CA上从C点运动到A点，速度为5 cm/s.若点P，Q分别从B，C同时运动：1解：∵在△ABC中，BC＝7 cm，AC＝24 cm，AB＝25 cm，72＋242＝252，∴BC2＋AC2＝AB2. ∴∠ACB＝90°.设y s后，S△PCQ的面积为15 cm2，根据题意可得BP＝2y cm，CQ＝5y cm，∴CP＝BC－BP＝(7－2y)cm，(1)经过多少秒后，S△PCQ的面积为15 cm2?(2)请用配方法说明，何时△PCQ的面积最大，最大面积是多少？2如图①放置两个全等的含有30°角的直角三角尺ABC与DEF(∠B＝∠E＝30°)，若将三角尺ABC向右以每秒1个单位长度的速度移动(点C与点E重合时移动终止)，移动过程中始终保持点B，F，C，E在同一条直线上，(1)在移动过程中，试用含x的代数式表示△AMQ的面积．解：∵在Rt△ABC中，∠B＝30°，∴∠BAC＝60°.∵∠E＝30°，∴∠EQC＝∠AQM＝60°.∴△AMQ为等边三角形．∴AM＝AQ.如图，过点M作MN⊥AQ，垂足为N，则AN＝QN.(2)计算x等于多少时，两个三角尺重叠部分的面积有最大值，最大值是多少？ 【点方法】用二次函数的性质求解几何图形面积的最值，通常先根据图形的特点，结合相关的几何性质，运用“面积法”建立函数关系式，再运用求二次函数最值的方法求解．3【2023·天津】如图，要围一个矩形菜园ABCD，其中一边AD是墙，且AD的长不能超过26 m，其余的三边AB，BC，CD用篱笆，且这三边的和为40 m，有下列结论：①AB的长可以为6 m；②AB的长有两个不同的值满足菜园ABCD的面积为192 m2；③菜园ABCD面积的最大值为200 m2.其中，正确结论的个数是(　　)A．0 B．1 C．2 D．3【点拨】【答案】 C4【母题：教材P44例2】如图，用一段长为30 m的篱笆围成一个一边靠墙、中间隔有一道篱笆的矩形菜园，墙长为18 m．设垂直于墙的边长为x m，菜园的面积为y m2.解：依题意得，矩形的另一边长为(30－3x)m，则y＝x(30－3x)＝－3x2＋30x，即y与x的函数表达式为y＝－3x2＋30x.(1)求y与x的函数表达式；解：当y＝75时，－3x2＋30x＝75，即x2－10x＋25＝0，解得x1＝x2＝5，∴当x＝5时，菜园的面积为75 m2.(2)当x为何值时，菜园的面积为75 m2；(3)能围成的面积比75 m2更大的菜园吗？如果能，请求出最大面积，并说明围法．如果不能，请说明理由．则抛物线开口向下，当x＝5时，y有最大值75，∴不能围成面积比75 m2更大的菜园，即最大面积为75 m2，此时垂直于墙的边长为5 m，平行于墙的一边长为30－3×5＝15(m)．5【2023·菏泽】 【情境题·生活应用】某学校为美化学校环境，打造绿色校园，决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园，用一道篱笆把花园分为A，B两块(如图所示)，花园里种满牡丹和芍药．学校已定购篱笆120米．解：设垂直于墙的边长为x米，围成的矩形花园的面积为S平方米，则平行于墙的边为(120－3x)米，根据题意得S＝x(120－3x)＝－3x2＋120x＝－3(x－20)2＋1 200，(1)设计一个使花园面积最大的方案，并求出其最大面积；∵－3＜0，∴当x＝20时，S取最大值1 200，∴120－3x＝120－3×20＝60，∴当垂直于墙的边长为20米，平行于墙的边长为60米时，花园面积最大，为1 200平方米； (2)在花园面积最大的条件下，A，B两块分别种植牡丹和芍药，每平方米种植2株，已知牡丹每株售价25元，芍药每株售价15元，学校计划购买费用不超过5万元，求最多可以购买多少株牡丹？解：设购买牡丹m株，则购买芍药1 200×2－m＝(2 400－m)株，∵学校计划购买费用不超过5万元，∴25m＋15(2 400－m)≤50 000，解得m≤1 400，∴最多可以购买1 400株牡丹．6有一块矩形地块ABCD，AB＝20米，BC＝30米．为了美观，拟种植不同的花卉，如图所示，将矩形ABCD分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为x米．现决定在等腰梯形AEHD和等腰梯形BCGF中种植甲种花卉；在等腰梯形ABFE和等腰梯形CDHG中种植乙种花卉；在矩形EFGH中种植丙种花卉．甲、乙、丙三种花卉的种植成本分别为20元/平方米、60元/平方米、40元/平方米，设三种花卉的种植总成本为y元．(1)当x＝5时，求种植总成本； (2)求y与x的函数表达式，并写出自变量x的取值范围；(3)若甲、乙两种花卉的种植面积之差不超过120 平方米，求三种花卉的最低种植总成本．∴－2x2＋60x－(－2x2＋40x)≤120，解得x≤6，∴0＜x≤6.∵y＝－400x＋24 000，∴y随x的增大而减小．∴当x＝6时，y最小，最小值为21 600，∴三种花卉的最低种植总成本为21 600元．