专题6-3立体几何大题综合归类（12题型+解题攻略）-2024年高考数学二轮热点题型归纳与变式演练（新高考通用）.zip

这是一份专题6-3立体几何大题综合归类（12题型+解题攻略）-2024年高考数学二轮热点题型归纳与变式演练（新高考通用）.zip，文件包含专题6-3立体几何大题综合归类原卷docx、专题6-3立体几何大题综合归类解析docx等2份试卷配套教学资源，其中试卷共94页， 欢迎下载使用。
TOC \ "1-1" \h \u \l "_Tc31183" 题型01平行：无交线型 PAGEREF _Tc31183 \h 1
\l "_Tc15411" 题型02平行：线面平行探索性 PAGEREF _Tc15411 \h 5
\l "_Tc19920" 题型03平行：面面平行探索性 PAGEREF _Tc19920 \h 8
\l "_Tc30670" 题型04 垂直：线面垂直探索性 PAGEREF _Tc30670 \h 10
\l "_Tc25026" 题型05垂直：面面垂直翻折探索性 PAGEREF _Tc25026 \h 14
\l "_Tc7885" 题型06证明与建系：斜棱柱垂面法建系 PAGEREF _Tc7885 \h 17
\l "_Tc7905" 题型07证明与建系：斜棱柱垂线法建系 PAGEREF _Tc7905 \h 20
\l "_Tc16696" 题型08 证明与建系：三棱柱投影法建系 PAGEREF _Tc16696 \h 24
\l "_Tc23017" 题型09 证明与建系：角平分线法建系 PAGEREF _Tc23017 \h 27
\l "_Tc6755" 题型10二面角延长线法 PAGEREF _Tc6755 \h 31
\l "_Tc23619" 题型11翻折型 PAGEREF _Tc23619 \h 34
\l "_Tc25583" 题型12台体型 PAGEREF _Tc25583 \h 38
\l "_Tc8054" 高考练场 PAGEREF _Tc8054 \h 42

题型01平行：无交线型
【解题攻略】
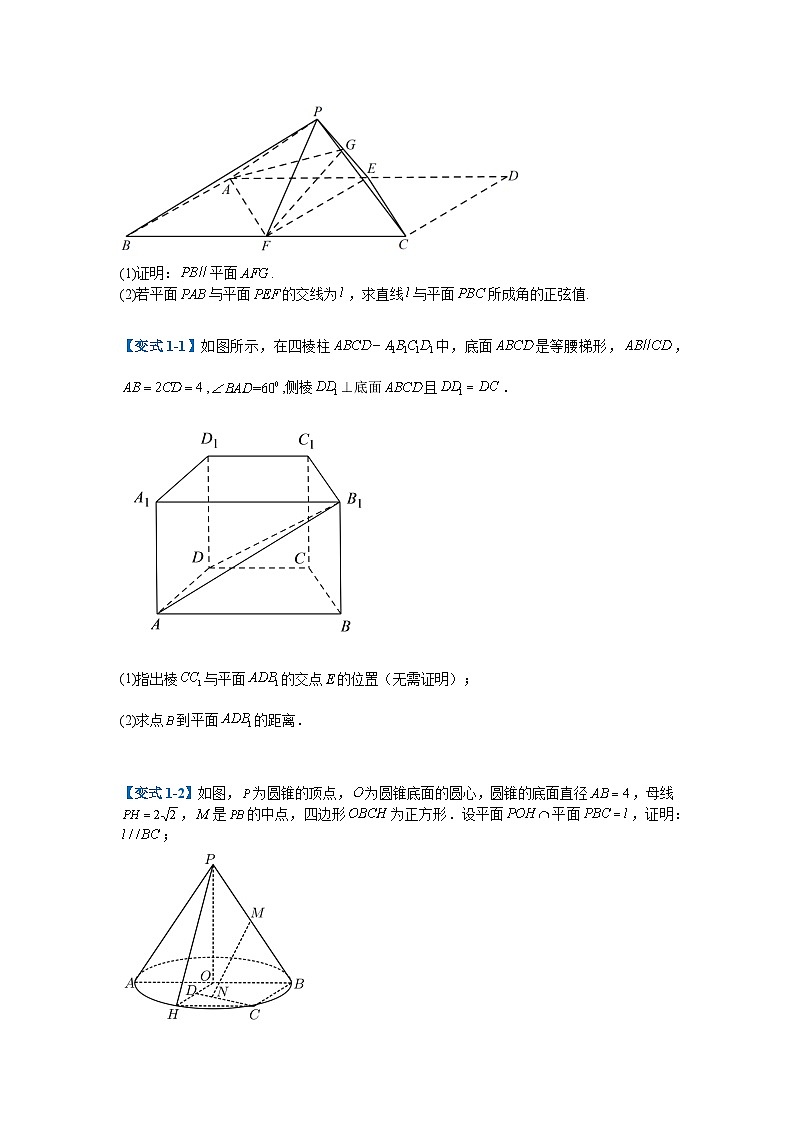
【典例1-1】如图，在平行四边形中，，，为的中点，以为折痕将折起，使点到达点的位置，且，，分别为，的中点.
(1)证明：平面.
(2)若平面与平面的交线为，求直线与平面所成角的正弦值.
【答案】(1)证明见解析；(2).
【分析】（1）连接，交于，并连接，易得为正方形，进而知为中位线，则，最后根据线面平行的判定证结论；
（2）若为中点，连接，由线面、面面垂直的判定可证面面，从而在面上的射影在直线上，过作直线则有直线为面与面的交线，故与面所成角即为所求角，再根据已知、等体积法求到面的距离，即可求角的正弦值.
（1）
连接，交于，并连接，
由、分别是、的中点，而，故为正方形，
所以为的中点，又是的中点，
所以，而面，面，故面.
（2）
由题易知：且均为等腰三角形，且均为等边三角形，
若为中点，连接，则，
而，面，则面，
又面，故面面，面面，
所以在面上的射影在直线上，
过作直线，而，则，故直线为面与面的交线，
所以直线与平面所成角，即为与面所成角，
由题设，，，令，则，，
因为面，面，故，
所以，又，易知，
在△中，，整理得，
所以，故，，
若到面的距离为，且，即，
所以，，，，
综上，，则.
【变式1-1】如图所示，在四棱柱中，底面是等腰梯形，，,,侧棱⊥底面且．
(1)指出棱与平面的交点的位置（无需证明）；
(2)求点到平面的距离．
【答案】(1)点位于的中点位置，理由见解析；
(2).
【分析】（1）作出辅助线，得到四棱柱为长方体，利用中位线得到线线平行，得到棱与平面的交点的位置为的中点；
（2）利用等体积法求解点到平面的距离.
（1）
延长至点F，且DF=CD，延长至点H，使得，连接FH，交于点Q，
因为四棱柱中，底面是等腰梯形，，
所以四棱柱为长方体，，且为的中点，
取的中点E，连接ED，则，
所以，
故棱与平面的交点的位置为的中点；
（2）
取AB的中点M，连接DM，
因为,,
故△ADM为等边三角形，
所以，
因为侧棱⊥底面且，平面，
所以，
由勾股定理得：，
由余弦定理得：，
其中，
，
由余弦定理得：，
因为，
所以，
由三角形面积公式可知：，
设点到平面的距离为，
因为，即，
，解得：，
所以点到平面的距离为.
【变式1-2】如图，为圆锥的顶点，为圆锥底面的圆心，圆锥的底面直径，母线，是的中点，四边形为正方形．设平面平面，证明：；
【答案】证明见解析.
【分析】利用线面平行的判定定理可得平面，再利用线面平行的性质定理即得.
【详解】因为四边形为正方形，
∴，
∵平面，平面，
∴平面，
∵平面，平面平面，
∴．
.
题型02平行：线面平行探索性
【解题攻略】
【典例1-1】如图，在三棱柱中，侧面底面，，，且，为中点.
(1)求证平面
(2)在上是否存在一点，使得平面，若不存在，说明理由；若存在，确定点E的位置.
【答案】(1)证明见解析。(2)存在，E为线段BC1的中点
【分析】（1）利用线面垂直的判定定理进行证明即可；
（2）连接，交于，连接，能够判断OM平面A1AB，BC1的中点M即为所求的E点.
（1）证明：连接，，且为的中点，所以.
，且为的中点，∴A1O⊥AC.又，平面，平面，
∴平面．
（2）存在点E，且E为线段BC1的中点.理由：连接，交于，连接，则OM是的一条中位线，OMAB1，
又平面，OM⊄平面A1AB，∴OM平面A1AB，故BC1的中点M即为所求的E点.
【变式1-1】如图，四边形中，，，，，，分别在，上，，现将四边形沿折起，使．
(1)若，在折叠后的线段上是否存在一点，使得平面？若存在，求出的值；若不存在，说明理由.
(2)求三棱锥的体积的最大值，并求出此时点到平面的距离.
【答案】(1)存在，
(2)三棱锥A­CDF的体积的最大值为3，此时点F到平面ACD的距离为
【分析】(1)在AD上取一点P，使得，证明线面平行，则P点就是所求的点；
(2)先设 ，运用二次函数即可求出三棱锥 的体积最大值，再运用等体积法求出F到平面ACD的距离.
（1）
AD上存在一点P，使得CP 平面ABEF，此时，
理由如下：当时，，如图，过点P作M FD交AF于点M，连接ME，则，
∵BE＝1，∴FD＝5，∴MP＝3，又EC＝3，MP FD EC，∴MP EC，
故四边形MPCE为平行四边形，∴CP ME，又CP⊄平面ABEF，ME⊂平面ABEF，
∴CP 平面ABEF；
（2）设BE＝x，则AF＝x(0