题型04 多边形证明 类型二 特殊四边形证明（专题训练）-最新中考数学二轮复习讲义+专题（全国通用）

这是一份题型04 多边形证明 类型二 特殊四边形证明（专题训练）-最新中考数学二轮复习讲义+专题（全国通用），文件包含题型四多边形证明类型二特殊四边形证明专题训练原卷版docx、题型四多边形证明类型二特殊四边形证明专题训练解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
1、以专题复习为主。如选择题、填空题的专项练习，要把握准确度和时间的安排。加强对二次函数与几何图形结合的综合性试题、实际应用题等专题的练习，深化对常考题型的熟悉程度。
2、重视方法思维的训练。对初中数学所涉及的函数思想、方程思想、数形结合思想、分类讨论思想、转化与化归思想、整体思想等数学思想方法，要通过典型试题的训练，进一步渗透和深刻理解其内涵，重要处舍得投入时间与精力。强化解题过程中常用的配方法、待定系数法等通法。
3、拓宽思维的广度，培养多角度、多维度思考问题的习惯。将专项复习中的共性习题串连起来，通过一题多解，积极地探求解决问题的最优解法，这样，对于解决难度较大的压轴题会有很大的帮助。
题型四 多边形证明
类型二 特殊四边形证明（专题训练）
1.如图，点E，F分别在菱形ABCD的边BC，CD上，且BE＝DF．求证：∠BAE＝∠DAF．
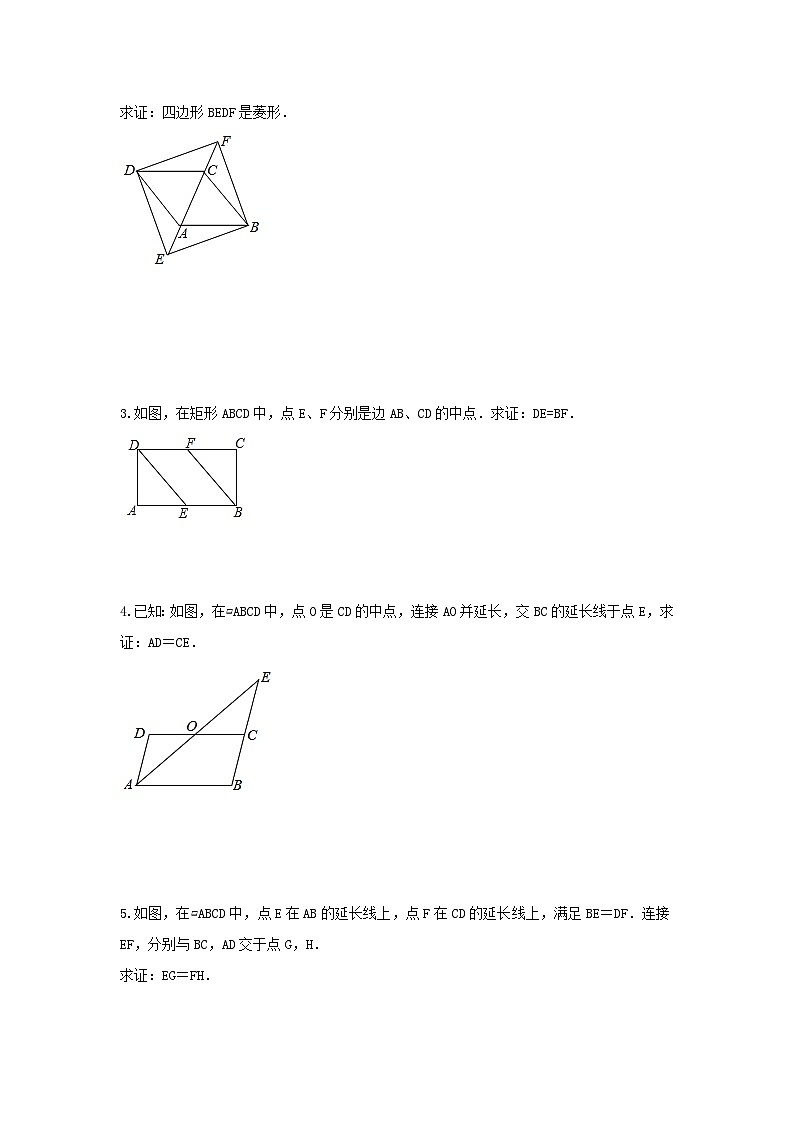
2.如图，在菱形ABCD中，将对角线AC分别向两端延长到点E和F，使得AE＝CF．连接DE，DF，BE，BF．
求证：四边形BEDF是菱形．
3.如图，在矩形ABCD中，点E、F分别是边AB、CD的中点．求证：DE=BF．
4.已知：如图，在▱ABCD中，点O是CD的中点，连接AO并延长，交BC的延长线于点E，求证：AD＝CE．
5.如图，在▱ABCD中，点E在AB的延长线上，点F在CD的延长线上，满足BE＝DF．连接EF，分别与BC，AD交于点G，H．
求证：EG＝FH．
6.如图，▱ABCD的对角线AC、BD相交于点O，过点O作EF⊥AC，分别交AB、DC于点E、F，连接AF、CE．
（1）若OE=32，求EF的长；
（2）判断四边形AECF的形状，并说明理由．
7.已知：如图，在▱ABCD中，点E、F分别在AD、BC上，且BE平分∠ABC，EF∥AB．求证：四边形ABFE是菱形．
8.如图，四边形是菱形，点、分别在边、的延长线上，且．连接、．
求证：．
9.如图，在中，的角平分线交于点D，．
（1）试判断四边形的形状，并说明理由；
（2）若，且，求四边形的面积．
10.如图，矩形ABCD的对角线AC、BD相交于点O，，．
（1）求证：四边形AOBE是菱形；
（2）若，，求菱形AOBE的面积．
11.如图，点C是的中点，四边形是平行四边形．
（1）求证：四边形是平行四边形；
（2）如果，求证：四边形是矩形．
12.如图，在平行四边形ABCD中，对角线AC与BD相交于点O，过点O的直线EF与BA、DC的延长线分别交于点E、F．
（1）求证：AE＝CF；
（2）请再添加一个条件，使四边形BFDE是菱形，并说明理由．
13.如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE＝BF，连接AE，CF．
（1）求证：△ADE≌△CBF；
（2）连接AF，CE．当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．
14.如图，在平行四边形ABCD中，对角线AC，BD相交于点O，分别过点A，C作AE⊥BD，CF⊥BD，垂足分别为E，F．AC平分∠DAE．
（1）若∠AOE＝50°，求∠ACB的度数；
（2）求证：AE＝CF．
15.如图，在平行四边形ABCD中，AE，CF分别平分∠BAD和∠DCB，交对角线BD于点E，F．
（1）若∠BCF＝60°，求∠ABC的度数；
（2）求证：BE＝DF．
16.如图，点E是▱ABCD的边CD的中点，连结AE并延长，交BC的延长线于点F．
（1）若AD的长为2，求CF的长．
（2）若∠BAF＝90°，试添加一个条件，并写出∠F的度数．
17.如图，四边形ABCD是平行四边形，DE∥BF，且分别交对角线AC于点E，F，连接BE，DF．
（1）求证：AE＝CF；
（2）若BE＝DE，求证：四边形EBFD为菱形．
18.如图，点E，F在▱ABCD的边BC，AD上，BE=13BC，FD=13AD，连接BF，DE．
求证：四边形BEDF是平行四边形．
20.如图，在四边形ABCD中，AD∥BC，对角线BD的垂直平分线与边AD、BC分别相交于点M、N．
（1）求证：四边形BNDM是菱形；
（2）若BD＝24，MN＝10，求菱形BNDM的周长．