






所属成套资源:2023年中考数学一轮复习课件(含答案)
2023年中考数学一轮复习课件专题6.3 与圆有关的计算(含答案)
展开
这是一份2023年中考数学一轮复习课件专题6.3 与圆有关的计算(含答案),共22页。PPT课件主要包含了正多边形与圆,扇形的弧长与面积,圆锥的有关计算,外接圆的圆心,外接圆的半径,S侧πrl,π+2等内容,欢迎下载使用。
【例1】刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积S来近似估计圆O的面积,则S=_____.(结果保留根号)
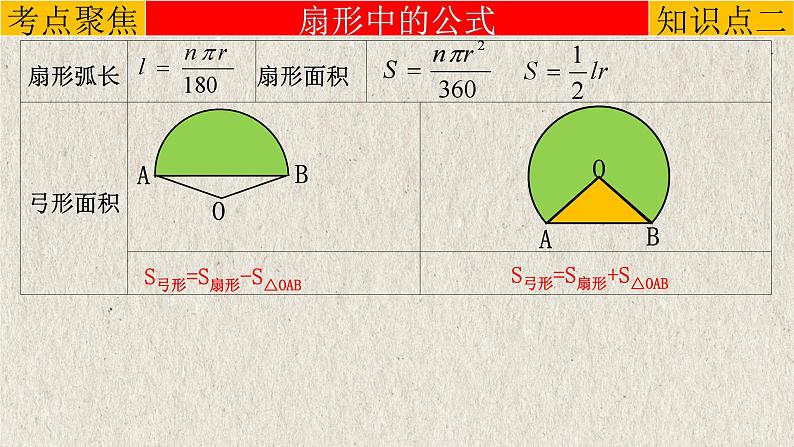
S弓形=S扇形+S△OAB
S弓形=S扇形-S△OAB
【例2-2】如图,半圆O´的直径CD在半圆O的直径AB上,半圆O的弦EF∥AB,EF与半圆O´相切,且EF=4,则图中的阴影部分的面积为______.
【例3】已知圆锥的侧面积是8πcm2,若圆锥底面半径为Rcm,母线长为lcm,则R关于l的函数图象大致是( )
【例2-2】如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为90º的扇形,则此扇形的面积为( ) A. B. C.πm2 D.2πm2
1.正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是____. 2.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为______.3.如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则S1:S2=_____.
4.如图,△ABC是正三角形,曲线CDEF…叫做“正三角形的渐开线”,其中CD,DE,EF,…的圆心按点A,B,C循环.如果AB=1,那么曲线CDEF的长是____.5.如图,△ABC中,BD=CD,以D为圆心,BD长为半径画弧交AC于E点,若∠A=60º,∠B=100º,BC=4,S扇形BDE=____. 6.如图,A,B,C,D,为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18º,则这个正多边形的边数为____.
1.如图,点C在以AB为直径的半圆上,∠ABC=30º.沿直线CB将半圆折叠,点A与点A´重合,A´B与弧BC交于点D.已知弧AC的长为π,则图中的阴影部分的面积为_______.
2.如图,某数学兴趣小组将长为6,宽为3的矩形铁丝框ABCD变形为以A为圆心AB为半径的扇形(忽略铁丝的粗细),则所得扇形AEB的面积为____.3.如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形.则所得扇形AFB(阴影部分)的面积为_____.
4.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120º.则图2的周长为_____cm5.如图,正方形ABCD对角线AC所在直线上有一点O,OA=3,AC=2,将正方形绕O点顺时针旋转90º,在旋转过程中,正方形扫过的面积是_______.
相关课件
这是一份中考数学一轮复习精品课件专题6.3 与圆有关的计算(含答案),共4页。PPT课件主要包含了正多边形与圆,扇形的弧长与面积,圆锥的有关计算,外接圆的圆心,外接圆的半径,S侧πrl,π+2等内容,欢迎下载使用。
这是一份中考数学一轮复习知识点梳理+提升训练精品课件专题6.3《与圆有关的计算》(含答案),共22页。PPT课件主要包含了正多边形与圆,扇形的弧长与面积,圆锥的有关计算,外接圆的圆心,外接圆的半径,S侧πrl,π+2等内容,欢迎下载使用。
这是一份专题19 与圆有关的计算课件-数学中考一轮复习,共21页。









