

福建省莆田市城厢区中山中学2023-2024学年九年级上学期第一次月考数学试卷(含答案)
展开1.(4分)下列函数关系中,y是x的二次函数的是( )
A.y=ax2+bx+cB.
C.y=50+x2D.y=(x+2)(x﹣3)﹣x2
2.(4分)将一元二次方程3x2+1=6x化为一般形式后,二次项系数和一次项系数分别为( )
A.3,﹣6B.3,6C.3,1D.3x2,﹣6x
3.(4分)如果将抛物线y=2x2﹣1向右平移一个单位,那么所得新抛物线的表达式为( )
A.y=2x2B.y=2x2﹣2
C.y=2(x+1)2﹣1D.y=2(x﹣1)2﹣1
4.(4分)某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315B.560(1﹣x)2=315
C.560(1﹣2x)2=315D.560(1﹣x2)=315
5.(4分)如图,在平面直角坐标系中△AOB与△COD是位似图形,以原点O为位似中心,若AC=2OA,B点坐标为(4,2),则点D的坐标为( )
A.(8,4)B.(8,6)C.(12,4)D.(12,6)
6.(4分)二次函数y=x2﹣6x﹣5配方,则其中变形正确的为( )
A.y=(x﹣3)2﹣4B.y=(x﹣3)2﹣14
C.y=(x+3)2﹣14D.y=(x+3)2﹣4
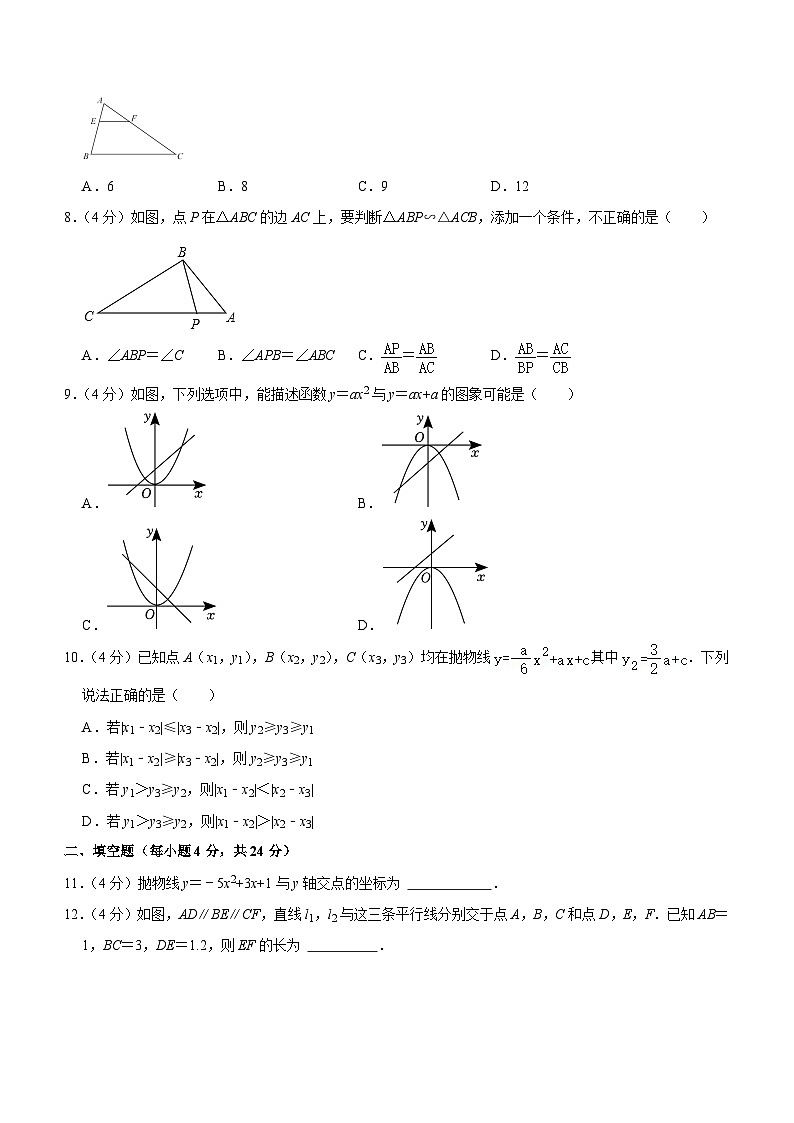
7.(4分)如图,在△ABC中,点E、F分别是AB、AC上的点,且EF∥BC,若S四边形BCFE=8,S△AEF=1,AF=3,则CF的长是( )
A.6B.8C.9D.12
8.(4分)如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠CB.∠APB=∠ABCC.=D.=
9.(4分)如图,下列选项中,能描述函数y=ax2与y=ax+a的图象可能是( )
A.B.
C.D.
10.(4分)已知点A(x1,y1),B(x2,y2),C(x3,y3)均在抛物线其中.下列说法正确的是( )
A.若|x1﹣x2|≤|x3﹣x2|,则y2≥y3≥y1
B.若|x1﹣x2|≥|x3﹣x2|,则y2≥y3≥y1
C.若y1>y3≥y2,则|x1﹣x2|<|x2﹣x3|
D.若y1>y3≥y2,则|x1﹣x2|>|x2﹣x3|
二、填空题(每小题4分,共24分)
11.(4分)抛物线y=﹣5x2+3x+1与y轴交点的坐标为 .
12.(4分)如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DE=1.2,则EF的长为 .
13.(4分)已知二次函数y=﹣x2+2x的图象上有两点A(﹣1,y1),B(3,y2),则y1,y2的大小关系为y1 y2.
14.(4分)已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是 .
15.(4分)如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=,则△ABC的边长为 .
16.(4分)如图,是抛物线图象的一部分,抛物线的顶点坐标为A(1,3),与x轴的一个交点为B(4,0),点A和点B均在直线y2=mx+n(m≠0)上.①2a+b=0;②abc>0;③抛物线与x轴的另一个交点是(﹣4,0);④方程ax2+bx+c=﹣3有两个不相等的实数根.其中正确的是 .(填写序号)
三、解答题(共86分)
17.(8分)解一元二次方程:x2﹣6x+8=0.
18.(8分)已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如表所示:
求这个二次函数的表达式.
19.(8分)如图,在△ABC和△DEC中,∠BCE=∠ACD,∠B=∠CED,求证:△ABC∽△DEC.
20.(8分)如图1,是抛物线形的拱桥,当拱顶高离水面2米时,水面宽4米.如图建立平面直角坐标系,解答下列问题:
(1)如图2,求该抛物线的函数解析式.
(2)当水面AB下降1米,到CD处时,水面宽度增加多少米?(保留根号)
(3)当水面AB上升1米时,水面宽度减少多少米?(保留根号)
21.(8分)已知抛物线y=x2+2mx﹣(m>0)
(1)求证:该抛物线与x轴必有两个交点;
(2)若抛物线与x轴的两个交点分别为A、B(点A在点B的左侧),且AB=6,求m的值.
22.(10分)如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点出发沿AB边向B以1cm/s的速度移动,点Q从B点出发沿BC向C点以2cm/s的速度移动,当其中一个点到达终点时两个点同时停止运动,请回答:
(1)经过多少时间,△PBQ的面积是5cm2,此时,PQ长为多少cm;
(2)探究:是否存在某一时刻t,使?如果存在,求出t的值;如果不存在,请说明理由.
23.(10分)某网店3月份经营一种热销商品,每件成本20元,发现三周内售价在持续提升,销售单价P(元/件)与时间t(天)之间的函数关系为P=30+t(其中1≤t≤21,t为整数),且其日销售量y(件)与时间t(天)的关系如下表
(1)已知y与t之间的变化规律符合一次函数关系,请直接写出y(件)与时间t(天)函数关系式;
(2)在这三周的销售中,第几天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的21天中,该网店每销售一件商品就捐赠a元利润(a<8)给“精准扶贫”的对象,通过销售记录发现,这21天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
24.(12分)已知,抛物线y=﹣x2+bx+c经过B(3,0)、C(0,3)两点,点P是抛物线上一点,点A是抛物线与x轴的另一个交点.
(1)求抛物线的解析式;
(2)当点P位于第一象限时,连接BP,CP,得到△BCP,当△BCP的面积最大时,求点P的坐标;
(3)当点P位于第四象限时,连接AC,BC,PC,若∠PCB=∠ACO,求直线PC的解析式.
25.(14分)已知,如图,在四边形ABCD中,∠ABC=∠ADC=90°,连接AC,过点B作BM⊥AC于点E,交CD于点M.
(1)求作直线DM,满足DN∥BM,分别交AC,AB于点F、M;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,
①求证:DF•ME=BE•NF;
②连接BD,MN,求证:直线AC、BD、MN相交于同一点.
参考答案
一、选择题(每小题4分,共40分)
1.C;2.A;3.D;4.B;5.D;6.B;7.A;8.D;9.A;10.D;
二、填空题(每小题4分,共24分)
11.(0,1);12.3.6;13.=;14.﹣1<x<3;15.3;16.①④;
三、解答题(共86分)
17.x1=2,x2=4.;
18.解:由题意可得二次函数的顶点坐标为(-1,-4),
设二次函数的解析式为:y=a(x+1)2-4,
把点(0,-3)代入y=a(x+1)2-4,得a=1,
故抛物线解析式为y=(x+1)2-4,即y=x2+2x-3.;
19.证明:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠ACB=∠DCE,
∵∠B=∠CED,
∴△ABC∽△DEC..;
20.(1)y=﹣x2;(2)水面宽度增加(2﹣4)米;(3)水面宽度减少(4﹣2)米.;
21.(1);(2)2.;22.(1)1秒,;(2)不存在某一时刻t,使.;23. (1)y=-2t+120;
(2)第10天的销售利润最大,最大利润是1250元;
(3)即a的取值范围是5.25≤a<8.;
24.(1)y=﹣x2+2x+3;(2);(3)直线PC的解析式为y=﹣2x+3.;、25.(1).(2)①.②;
x
……
﹣3
﹣2
﹣1
0
1
……
y
……
0
﹣3
﹣4
﹣3
0
……
时间t(天)
1
5
9
13
17
21
日销售量y(件)
118
110
102
94
86
78
2023-2024学年福建省莆田市城厢区九年级上学期数学第一次月考试题及答案: 这是一份2023-2024学年福建省莆田市城厢区九年级上学期数学第一次月考试题及答案,共19页。试卷主要包含了 我们给出定义等内容,欢迎下载使用。
福建省莆田市城厢区砺成中学2023-2024学年九上数学期末监测模拟试题含答案: 这是一份福建省莆田市城厢区砺成中学2023-2024学年九上数学期末监测模拟试题含答案,共8页。试卷主要包含了如图,已知等内容,欢迎下载使用。
2023-2024学年福建省莆田市城厢区文献中学九年级(上)期中数学试卷(含解析): 这是一份2023-2024学年福建省莆田市城厢区文献中学九年级(上)期中数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












