第六章实数总复习课件

这是一份第六章实数总复习课件，共24页。

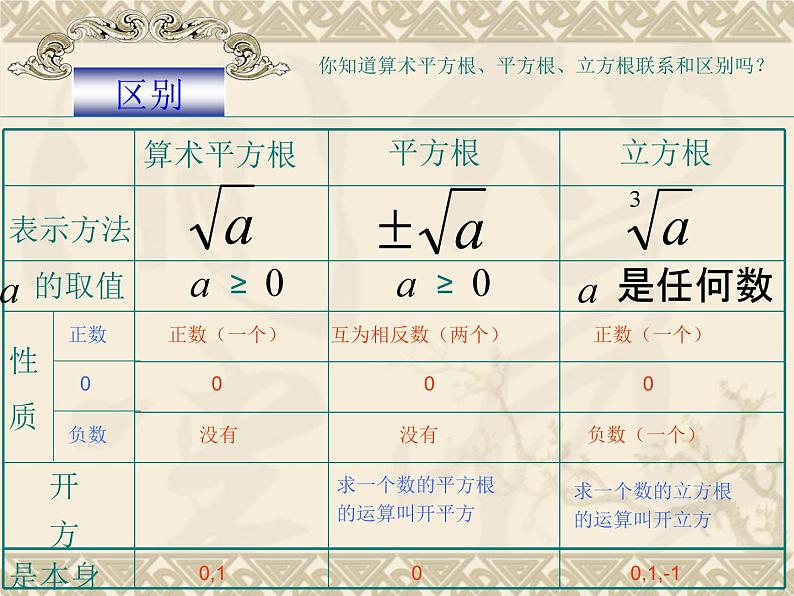
第六章实数复习特殊：0的算术平方根是0。1.算术平方根的定义：一般地，如果一个数的平方等于a ，那么这个数就叫做a 的平方根（或二次方根）．　这就是说，如果x 2 = a ，那么 x 就叫做 a 的平方根．a的平方根记为± 2. 平方根的定义：3.平方根的性质：正数有2个平方根，它们互为相反数；0的平方根是0；负数没有平方根。4.立方根的定义： 一般地，如果一个数的立方等于a，那么这个数就叫做a的立方根，也叫做a的三次方根．记作　　 5.立方根的性质：你知道算术平方根、平方根、立方根联系和区别吗？表示方法性质开方正数0负数正数（一个）0没有互为相反数（两个）0没有正数（一个）0负数（一个）求一个数的平方根的运算叫开平方求一个数的立方根的运算叫开立方是本身0,100,1,-1练习：1、—8是 的平方根, 64的平方根是 ； 的平方根是 。2、 的立方根是（ ）， 3 的平方根是 （ ）X=71464±88-432-64的立方根是_____ =几个基本公式：（注意字母的取值范围）= -练习：； 解：原式＝-a+a =0解：原式＝n-m+n-m =2n-2m无限不循环的小数 叫做无理数.在进行实数的运算时，有理数的运算法则及运算性质同样适用。有理数和无理数统称实数.实数与 上的点是一一对应的在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样数轴实数有理数无理数分数整数正整数 0负整数正分数负分数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况实数的分类1、判断下列说法是否正确：1.实数不是有理数就是无理数。 （ ）2.无限小数都是无理数。 （ ）3.无理数都是无限小数。 （ ）4.带根号的数都是无理数。 （ ） 5.两个无理数之和一定是无理数。（ ）6.所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数。（ ）练习2.把下列各数分别填入相应的集合内：（相邻两个3之间的7的个数逐次加1） 有理数集合 无理数集合不要遗漏2.解方程：当方程中出现平方时，若有解，一般都有两个解当方程中出现立方时，一般都有一个解(1).解:(2).解:1.已知 和 的和为0,则x的范围是为( )A.任意实数 B.非正实数 C .非负实数 D. 02.若- = ,则m的值是 ( ) A B C D3. 若 成立,则x的取值范围是( ) A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数 4.若 =4-x成立,则x的取值范围是( ) A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数 BBAD四、知识提高1、已知， （3）0.03的平方根约为 ；（4）若 2、已知，，，求（1） （2）3000的立方根约为 ； （3），则 17.320.54770.173230000.669414.42300003、若，则x的取值范围是 ___ 4、已知位置如图所示，试化简 x≤2解：原式＝-a-(b-a)+(c-a)-(c-b)=-a-b+a+c-a-c+b=-a5、已知的小数部分为m,，的小数部分为n 6、计算：1解：原式＝1.2+0.4+1-2 ＝0.6解：原式＝3+5-1+4 ＝11五、强化运用1、下列说法正确的是( )A、B 表示6的算术平方根的相反数C、 任何数都有平方根 D、一定没有平方根B-5x≤0X为任何实数6、已知，求的值。7、已知，求 y-x的算术平方根解：由题意得：｛｛a-4≥0解得a≥4∴ a-3+∴a-4=9∴a=13解：由题意，得：X-2≥02-x≥0解得：x≥2x≤2∴x=2当x=2时，y=3掌握规律1011、若为实数，则下列命题正确的是（ ） B、C、 D、 A、12. 若 成立,则x的取值范围是( ) A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数 13 .若 =4-x成立,则x的取值范围是( ) A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数 ADB1.如果一个数的平方根为a+1和2a-7, 求这个数2、 的平方根是＿ ＿ ＿ ＿ ＿ ，3-2的算术平方根是＿ ＿ ＿ ＿ ＿ ，立方根为其本身的实数＿ ＿ ＿ ＿ ＿。