中考数学模拟试卷及答案

这是一份中考数学模拟试卷及答案，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．|－2|的值是（ ）
2．已知某种纸一张的厚度约为0.0089cm，用科学记数法表示这个数为（ ）
3．计算a3·(－a)2的结果是（ ）
4．如图，矩形ABCD的边AD长为2，AB长为1，点A在数轴上对应的数是－1，以A点为圆心，对角线AC长为半径画弧，交数轴于点E，则点E表示的实数是（ ）

5．已知一次函数y＝ax－x－a＋1(a为常数)，则其函数图象一定过象限 （ ）
6. 在△ABC中， AB＝3，AC＝2．当∠B最大时，BC的长是 （ ）
A．1 B．5 C． eq \r(13) D． eq \r(5)
二、填空题（本大题共10小题，每小题2分，共20分）
7．计算： ．
8．因式分解：a3－4a＝ ．
9．计算： eq \f(3－ EQ \r( ,3), EQ \r( ,3)) ＝ ．
10．函数y＝ eq \f( eq \r(x－1),2)中，自变量x的取值范围是 ．
11.某商场统计了去年1～5月A，B两种品牌冰箱的销售情况.
则这段时间内这两种品牌冰箱月销售量较稳定的是 （填“A”或“B”）.
（第15题）
（第12题）
1
2
12．如图，将三角板的直角顶点放在直尺的一边上，若∠1＝55°，则∠2的度数为 °.
13．已知m、n是一元二次方程ax2–2x＋3＝０的两个根，若m＋n＝2，则mn＝ ．
14．某小组计划做一批中国结，如果每人做6个，那么比计划多做了9个；如果每人做4个，那么比计划少7个.设计划做x个中国结，可列方程 ．
15. 如图所示的“六芒星”图标是由圆的六等分点连接而成，若圆的半径为2 EQ \r( ,3)，则图中阴影部分的面积为 ．
16．已知二次函数y＝ax2＋bx＋c与自变量x的部分对应值如下表：
现给出下列说法：①该函数开口向下． ②该函数图象的对称轴为过点（1，0）且平行于y轴的直线．
③当x＝2时，y＝3． ④方程ax2＋bx＋c＝﹣2的正根在3与4之间．
其中正确的说法为 ．（只需写出序号）
三、解答题（本大题共12小题，共88分）
17. （6分）解不等式：1－ eq \f(2x－1,3) eq \f(1－x,2) ，并写出它的所有正整数解.
18．（6分）化简： eq \f(x－3,x－2) ÷（ x＋2－ eq \f(5,x－2) ）.
19.（8分）（1）解方程组 eq \b\lc\{(\a\al(y＝x＋1，,3x－2y＝－1；)) （2）解方程组eq \b\lc\{(\a\al(x＋y＝1，,x＋y2＝3．))
20．全国12-35岁的网瘾人群分布条形统计图
全国12-35岁的网瘾人群分布扇形统计图
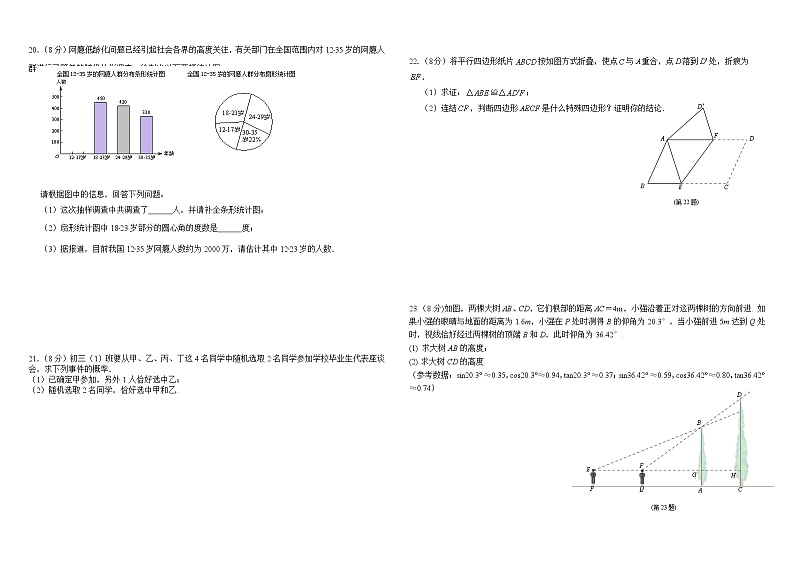
（8分）网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查，绘制出以下两幅统计图．
请根据图中的信息，回答下列问题：
（1）这次抽样调查中共调查了 人，并请补全条形统计图；
（2）扇形统计图中18﹣23岁部分的圆心角的度数是 度；
（3）据报道，目前我国12﹣35岁网瘾人数约为2000万，请估计其中12﹣23岁的人数．
21．（8分）初三（1）班要从甲、乙、丙、丁这4名同学中随机选取2名同学参加学校毕业生代表座谈会，求下列事件的概率．
（1）已确定甲参加，另外1人恰好选中乙；
（2）随机选取2名同学，恰好选中甲和乙.
22.（8分）将平行四边形纸片按如图方式折叠，使点与重合，点落到处，折痕为．
A
D
B
E
C
D'
F
(第22题)
（1）求证：；
（2）连结，判断四边形是什么特殊四边形？证明你的结论．
23.（8分)如图，两棵大树AB、CD，它们根部的距离AC＝4m，小强沿着正对这两棵树的方向前进. 如果小强的眼睛与地面的距离为1.6m，小强在P处时测得B的仰角为20.3°，当小强前进5m达到Q处时，视线恰好经过两棵树的顶端B和D，此时仰角为36.42°.
(1) 求大树AB的高度；
求大树CD的高度.
(第23题)
A
B
P
E
D
C
Q
F
H
G
（参考数据：sin20.3°≈0.35，cs20.3°≈0.94，tan20.3°≈0.37；sin36.42°≈0.59，cs36.42°≈0.80，tan36.42°≈0.74）
24.（10分）把一根长80cm的铁丝分成两个部分，分别围成两个正方形.
（1）能否使所围的两个正方形的面积和为250cm2，并说明理由；
（2）能否使所围的两个正方形的面积和为180cm2，并说明理由；
（3）怎么分，使围成两个正方形的面积和最小？
25. （9分）如图，正比例函数y＝2x的图象与反比例函数y＝ eq \f(k,x) 的图象交于点A、B， AB＝2 EQ \R(,5) ．
（１）求k的值；
（２）若反比例函数y＝ eq \f(k,x) 的图象上存在一点C，则当△ABC为直角三角形，请直接写出点C的坐标．
x
y
O
A
B
(第25题)
26.（9分）如图，在⊙O的内接四边形ACDB中，AB为直径，AC：BC＝1：2，点D为弧AB的中点，BE⊥CD垂足为E.
（1）求∠BCE的度数；
（2）求证：D为CE的中点；
（第26题）
O
E
D
C
B
A
（3）连接OE交BC于点F，若AB＝ eq \r(10) ，求OE的长度.
27.（8分）在△ABC中，用直尺和圆规作图（保留作图痕迹）．
（图1）
A
C
B
（1）如图①，在AC上作点D，使DB +DC＝AC.
（2）如图②，作△BCE，使∠BEC＝∠BAC，CE＝BE； （图2）
A
C
B
(图3）
A
C
B
（3）如图③，已知线段a，作△BCF，使∠BFC＝∠A，BF＋CF＝a.
江苏省南京市中考数学模拟试卷(10)答案
一、选择题（每小题2分，共12分）
二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
7．10 8．a（a＋2）（a－2） 9． EQ \r( ,3)－1 10．x ≥ 1 11．A
12. 35° 13. 3 14. eq \f(x+9,6) = eq \f(x—7,4) 15．12 EQ \r( ,3) 16．①③④
三、解答题（本大题共12小题，共计88分）
17. （6分）
解：去分母，得：6－2(2x＋1)≥3(1－x) ……………………………2分
去括号，得：6－4x＋2≥3－3 x ……………………………3分
移项，合并同类项得：－x≥－5 ……………………………4分
系数化成1得：x≤5. ……………………………5分
它的所有正整数解1，2，3，4，5. ……………………………6分
18．（6分）
解：原式＝ eq \f(x－3,x－2) ÷（ eq \f(x2－4,x－2)－ eq \f(5,x－2) ）……………………………………………………2分
＝ eq \f(x－3,x－2) ÷ eq \f(x2－9,x－2) ……………………………………………3分
＝ eq \f(x－3,x－2) × eq \f(x－2,x2－9) ……………………………………………4分
＝ eq \f(x－3,x－2) × eq \f(x－2,（x－3）（x＋3）) ……………………………………………5分
＝ eq \f(1,x＋3) ……………………………………………6分
19．（8分）
解：（1）将①代入②，得 3x－2(x＋1)＝－1．
解这个方程，得x＝1． ………………………………………………………1分
将x＝1代入①，得y＝2 . ……………………………………………………2分
所以原方程组的解是eq \b\lc\{(\a\al(x＝1，,y＝2．)) …………………………………………………3分
（2）由①，得x＝1－y．③
将③代入②，得1－y＋y2＝3． ……………………………………………5分
解这个方程，得y1＝2，y2＝－1． …………………………………………7分
将y1＝2，y2＝－1分别代入③，得x1＝－1，x2＝2．
所以原方程组的解是eq \b\lc\{(\a\al(x1＝－1，,y1＝2，))eq \b\lc\{(\a\al(x2＝2，,y2＝－1．)) ……………………………8分
20．（8分）
解：（1）1500，（图略）； ……………………………4分
（2）108° ……………………………6分
（3） ……………………………8分
21．（8分）
解：（1）从乙、丙、丁这三种等可能出现的结果中随机选1人，恰好选中乙的概率是 EQ \F(1,3)；……………………………………………………………………………………………3分
（2）恰好选中甲和乙的概率是 EQ \F(1,6).……………………………………………8分
(树状图或列表或枚举列出所有等可能结果3分，强调等可能1分，得出概率1分)
22. （8分）
（1）三角形全等的条件一个1分，结论1分 …………………4分
（2）四边形是菱形 …………………5分
证明： …………………8分
(证出平行四边形1分，证出邻边相等1分，结论1分 )
23. （8分)
（1）解：在Rt△BEG中，BG＝EG×tan∠BEG ……………………1分
在Rt△BFG中，BG＝FG×tan∠BFG ……………………2分
设FG＝x米，（x＋5）0.37＝0.74x,
解得x＝5， ……………………3分
BG＝FG×tan∠BFG＝0.74×5＝3.7 ……………………4分
AB＝AG＋BG＝3.7＋1.6＝5.3米 ……………………5分
答：大树AB的高度为5.3米.
（2）在Rt△DFG中，DH＝FH×tan∠DFG＝(5＋4)×0.74＝6.66米 ………………7分
CD＝DH＋HC＝6.66＋1.6＝8.26米 ……………………8分
答：大树CD的高度为8.26米.
24. (10分)
解：（1）设其中一个正方形的边长为x cm，则另一个正方形的边长为（20－x）cm，
由题意得： x2＋（20－x）2＝250 ………2分
解得x1＝5，x2＝15. ………3分
当x＝5时，4x＝20，4（20－x）＝60；
当x＝15时，4x＝60，4（20－x）＝20.
答：能，长度分别为20cm与60cm. ………4分
（2）x2＋（20－x）2＝180
整理：x2－20x＋110＝0， ………5分
∵b2－4ac＝400－440＝﹣40＜0， ………6分
∴此方程无解，即不能围成两个正方形的面积和为180cm2 ………7分
（3）设所围面积和为y cm2，
y ＝x2＋（20－x）2 ………8分
＝2 x2－40x＋400
＝2（ x－10）2＋200 …………………9分
当x＝10时，y最小为200. 4x＝40，4（20－x）＝40.
答：分成40cm与40cm，使围成两个正方形的面积和最小为200 cm EQ \s\up4(2). …10分
25. （9分）解：（1）过点A作AD⊥x轴，垂足为D，
由题意可知点A与点B关于点O中心对称，且AB＝2 EQ \R(,5) …………………1分
∴OA＝OB＝ EQ \R(,5) ， ………………2分
设点A的坐标为（a，2a），
在Rt△OAD中，∠ADO＝90°，由勾股定理得：
a 2＋（2a）2＝（ EQ \R(,5) ）2
解得a＝1 ………………4分
∴点A的坐标为（1，2），把A（1，2）代入y＝ eq \f(k,x)，解得k＝2，………………5分
O
E
D
C
B
A
F
（第26题）
（2） （2，1）（﹣2，﹣1）（4， eq \f(1,2)）（﹣4，﹣ eq \f(1,2)）………………9分
（反比例函数对称性、用相似或勾股定理）
26. （9分）（1）连接AD，
∵D为弧AB的中点，
∴AD＝BD，
∵AB为直径，
∴∠ADB＝90°，∴∠DAB＝∠DBA＝45°，
∴∠DCB＝∠DAB＝45°. …………………3分
（2）∵BE⊥CD，又∵∠ECB＝45°
∴∠CBE＝45°，∴CE＝BE，
∵四边形ACDB是圆O的内接四边形，
∴∠A＋∠BDC＝180°，又∵∠BDE＋∠BDC＝180°
∴∠A＝∠BDE， …………………4分
又∵∠ACB＝∠BED＝90°，
∴△ABC∽△DBE， …………………5分
∴DE:AC＝BE：BC，
∴DE:BE＝AC：BC＝1:2，
又∵CE＝BE，∴DE:CE＝1:2，
∴D为CE的中点. …………………6分
（3）连接CO，∵CO＝BO，CE＝BE，
∴OE垂直平分BC，
∴F为OE中点，
又∵O为BC中点，∴OF为△ABC的中位线，
∴OF＝ EQ \F(1,2)AC， …………………7分
∵∠BEC＝90°，EF为中线，
∴EF＝ EQ \F(1,2)BC， …………………8分
在Rt△ACB中，AC2＋BC2＝AB2，
∵AC:BC＝1:2,AB＝ eq \r(10) ，
∴AC＝ eq \r(2) ，BC＝2 eq \r(2) ，
∴OE＝OF＋EF＝1.5 eq \r(2) …………………9分
27.（8分）（1）作图正确 …………………3分
（2）作图正确…………………6分
（3）作图正确 (只要做出一个即可)…………………8分
A
B
E
C
A
B
C
A
B
C
F
F
A．2
B．﹣2
C． EQ \F(1,2)
D．－ EQ \F(1,2)
A．8.9×10－５
B．8.9×10－４
C．8.9×10－３
D．8.9×10－２
A．a5
B．－a5
C．a6
D．－a6
-3
-2
-1
2
1
0
A
B
E
C
D
3
(第４题)
A． eq \r(5) ＋1
B． eq \r(5) －1
C． eq \r(5)
D． 1－ eq \r(5)
A．一、二
B．二、三
C．三、四
D．一、四
A品牌(台)
15
17
16
13
14
B品牌(台)
10
14
15
16
20
…
0
1
3
…
y
…
1
3
1
…
题号
1
2
3
4
5
6
答案
A
C
A
Ｂ
D
D