中考数学模拟试卷及答案5套

这是一份中考数学模拟试卷及答案5套，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．下列实数中，无理数为( )
A．0.2 B.eq \f(1,2) C.eq \r(,2) D．2
2．“2014年至2016年，中国同‘一带一路’沿线国家贸易总额超过3万亿美元”，将数据3万亿美元用科学记数法表示为( )
A．3×1014美元 B．3×1013美元 C．3×1012美元 D．3×1011美元
3．如图，下面的几何体由三个大小相同的小立方块组成，则它的左视图是( )
4．函数y＝eq \f(\r(,x＋3),x－5)中自变量x的取值范围是( )
A．x≥－3 B．x≠5 C．x≥－3或x≠5 D．x≥－3且x≠5
5．一元二次方程x2－2x＝0的解是( )
A．0 B．2 C．0或－2 D．0或2
6．下列说法中，正确的有( )
①等腰三角形两边长为2和5，则它的周长是9或12；②无理数－eq \r(,3)在－2和－1之间；③六边形的内角和是外角和的2倍；④若a＞b，则a－b＞0.它的逆命题是假命题；⑤北偏东30°与南偏东50°的两条射线组成的角为80°.
A．1个 B．2个 C．3个 D．4个
7．某交警在一个路口统计的某时段来往车辆的车速情况如表：
则上述车速的中位数和众数分别是( )
A．50，8 B．49，50 C．50，50 D．49，8
8．正比例函数y1＝k1x与反比例函数y2＝eq \f(k2,x)的图象相交于A，B两点，其中点B的横坐标为－2，当y1＜y2时，x的取值范围是( )
A．x＜－2或x＞2 B．x＜－2或0＜x＜2 C．－2＜x＜0或0＜x＜2 D．－2＜x＜0或x＞2
9．已知关于x的分式方程eq \f(1－m,x－1)－1＝eq \f(2,1－x)的解是正数，则m的取值范围是( )
A．m＜4且m≠3 B．m＜4 C．m≤4且m≠3 D．m＞5且m≠6

10．农夫将苹果树种在正方形的果园内，为了保护苹果树不受风吹，他在苹果树的周围种上针叶树．在下图里，你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律：当n为某一个数值时，苹果树数量会等于针叶树数量，则n为( )
A．6 B．8 C．12 D．16
二、填空题(每小题3分，共24分)
11．分解因式m2＋2mn＋n2－1＝____________．
12．某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为________________．
13．如图，点A，B，C在⊙O上，CO的延长线交AB于点D，∠A＝50°，∠B＝30°，则∠ADC的度数为________．

第13题图 第14题图 第15题图
14．如图，将平行四边形ABCO放置在平面直角坐标系xOy中，O为坐标原点，若点A的坐标是(6，0)，点C的坐标是(1，4)，则点B的坐标是________．
15．如图，在正方形ABCD中，对角线BD的长为eq \r(,2).若将BD绕点B旋转后，点D落在BC延长线上的点D′处，点D经过的路径为弧DD′，则图中阴影部分的面积是________．
16．对于任意实数m、n，定义一种新运算m※n＝mn－m－n＋3，等式的右边是通常的加减和乘法运算，例如：3※5＝3×5－3－5＋3＝10.请根据上述定义可知6＜2※x＜7的解集为________．
17．如图，∠AOB是放置在正方形网格中的一个角，则cs∠AOB的值是________．

第17题图 第18题图
18．如图，AB＝4，射线BQ和AB互相垂直，点D是AB上的一个动点，点E在射线BQ上，BE＝eq \f(1,2)DB，作EF⊥DE，并截取EF＝DE，连接AF并延长交射线BQ于点C.设BE＝x，BC＝y，则y关于x的函数解析式为______________．
三、解答题(共66分)
19．(6分)计算：－22－eq \r(,12)＋|1－4sin60°|＋eq \b\lc\(\rc\)(\a\vs4\al\c1(π－\f(22,7)))eq \s\up12(0).
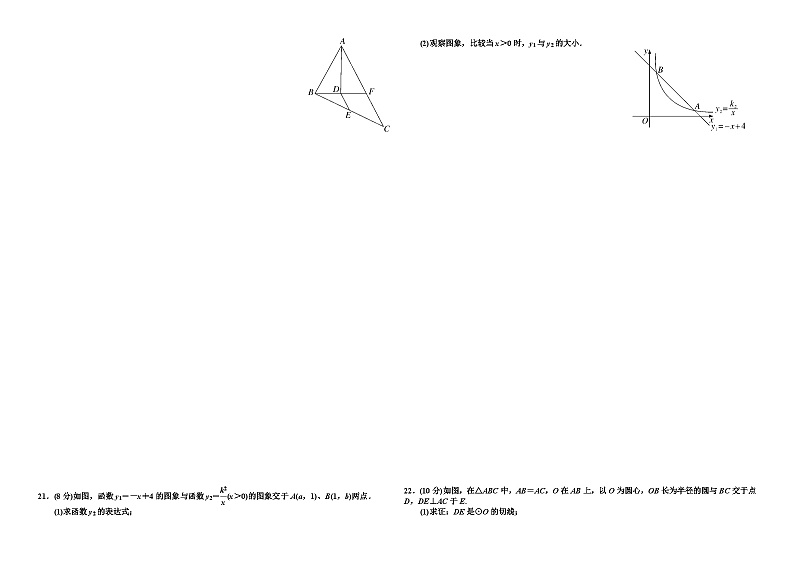
20．(8分)如图，在△ABC中，AB＝6cm，AC＝10cm，AD平分∠BAC，BD⊥AD于点D，BD的延长线交AC于 点F，E为BC的中点，求DE的长．
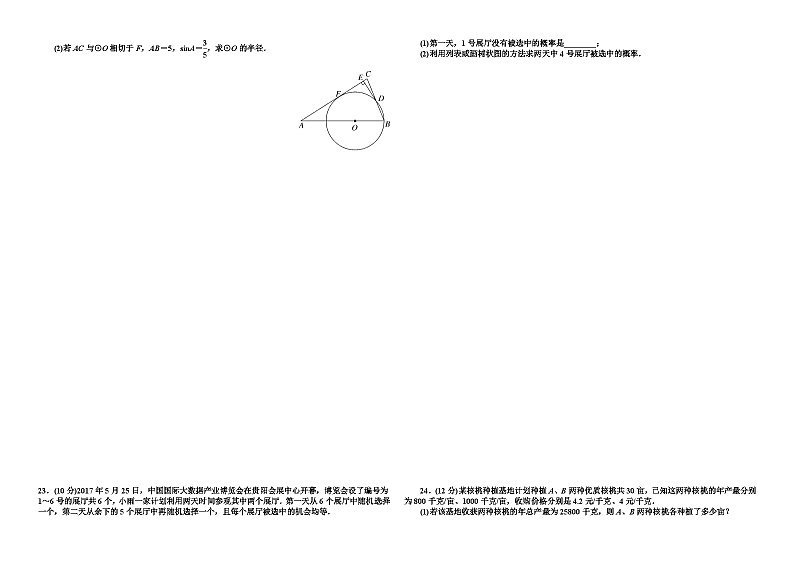
21．(8分)如图，函数y1＝－x＋4的图象与函数y2＝eq \f(k2,x)(x＞0)的图象交于A(a，1)、B(1，b)两点．
(1)求函数y2的表达式；
(2)观察图象，比较当x＞0时，y1与y2的大小．
22．(10分)如图，在△ABC中，AB＝AC，O在AB上，以O为圆心，OB长为半径的圆与BC交于点D，DE⊥AC于E.
(1)求证：DE是⊙O的切线；
(2)若AC与⊙O相切于F，AB＝5，sinA＝eq \f(3,5)，求⊙O的半径．
23．(10分)2017年5月25日，中国国际大数据产业博览会在贵阳会展中心开幕，博览会设了编号为1～6号的展厅共6个，小雨一家计划利用两天时间参观其中两个展厅．第一天从6个展厅中随机选择一个，第二天从余下的5个展厅中再随机选择一个，且每个展厅被选中的机会均等．
(1)第一天，1号展厅没有被选中的概率是________；
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率．
[来源:学.科.网]
24．(12分)某核桃种植基地计划种植A、B两种优质核桃共30亩，已知这两种核桃的年产量分别为800千克/亩、1000千克/亩，收购价格分别是4.2元/千克、4元/千克．
(1)若该基地收获两种核桃的年总产量为25800千克，则A、B两种核桃各种植了多少亩？
(2)设该基地种植A种核桃a亩，全部收购后，总收入为w元，求出w与a之间的函数关系式．若要求种植A种核桃的面积不少于B种核桃的一半，那么种植A、B两种核桃各多少亩时，该种植基地的总收入最多？最多是多少元？
25．(12分)如图①是一台放置在水平桌面上的笔记本电脑，将其侧面抽象成如图②所示的几何图形，若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm，点P为眼睛所在位置，D为AO的中点，连接PD，当PD⊥AO时，称点P为“最佳视角点”，作PC⊥BC，垂足C在OB的延长线上，且BC＝12cm.
(1)当PA＝45cm时，求PC的长；
(2)若∠AOC＝120°时，“最佳视角点”P在直线PC上的位置会发生什么变化？此时PC的长是多少？请通过计算说明(结果精确到0.1cm，可用科学计算器，参考数据：≈1.414，eq \r(,3)≈1.732)．
中考数学第一次模拟试卷（1）参考答案
1．C 2.C 3.C 4.D 5.D 6.B 7.C 8.B 9.A
10．B 解析：第1个图形中苹果树的棵数是1，针叶树的棵数是8；第2个图形中苹果树的棵数是4＝22，针叶树的棵数是16＝8×2，第3个图形中苹果树的棵数是9＝32，针叶树的棵数是24＝8×3，第4个图形中苹果树的棵数是16＝42，针叶树的棵数是32＝8×4，…，所以，第n个图形中苹果树的棵数是n2，针叶树的棵数是8n.∵苹果树的棵数与针叶树的棵数相等，∴n2＝8n，解得n1＝0(舍去)，n2＝8.故选B.
11．(m＋n－1)(m＋n＋1) 12.y＝a(1＋x)2 13.110°
14．(7，4) 15.eq \f(π,4)－eq \f(1,2) 16.53，则m的取值范围 （ ）
A、 B、 C、 D、
8、如图，四边形是菱形，过点作的平行线交的延长线于点，则下列式子不成立的是 …………………………………………………… ( )
A. B. C. ° D.
9、已知圆锥的侧面积是100πcm2，若圆锥底面半径为r（cm），母线长为L（cm），则L关于r的函数的图象大致是…………………………………………（ ）
r
l
O
r
O
r
l
O
r
O
A
B
C
D
l
l

10、如图，抛物线y＝ax2＋bx＋c与x轴交于A、B两点，满足a≥b，且B（2，0），则线段AB的最大值是 （ ）
A、3 B、4 C、5 D、6
A
B
C
B
A
O
x
y
二、填空题（本题有6小题，每小题4分，共24分）
11、天文学里常用“光年”作为距离单位。规定1“光年”为光在一年内传播的距离，大约等于94600亿千米，用科学计数法可表示为 千米。
12、多项式x2+1加上一个单项式后，可以分解因式，那么加上的单项式可以是 （只需填写二个）。
13、如图，一梯子AB斜靠在墙上，底端B距墙角BC＝1.5米，tan∠ABC＝3，则高度AC
＝ 米。
14、为了举行班级晚会，小王准备去商店购买20个乒乓球做道具，并买一些乒乓球拍做奖品，已知乒乓球每个1.5元，球拍每副22元，如果购买金额不超过200元，且买的球拍尽可能多，那么小王应该买 副球拍
15、等腰△ABC是⊙O的内接三角形，∠A＝45°，底边BC＝4，则弦BC所对弧长为 。
16、如图，A、B在坐标轴的正半轴上移动，且AB＝10，双曲线y＝（x＞0），
（1）当A（6, 0），B（0, 8），k＝12时，双曲线与AB交点坐标为 ；（2）如双曲线y＝与AB有唯一公共点P，点M在x轴上，△OPM为直角三角形，
当M从点（5, 0）移动到点（10, 0）时，动点P所经过的路程为
三、解答题（本题有8小题，共66分）
17（6分） （1）计算：30°－
（2）解方程：＋1＝
（直角三角形）
（等腰梯形）
（矩形）
18（6分）如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形的边长为2，是的中点，按将菱形剪成①、②两部分，用这两部可分以分别拼成直角三角形、等腰梯形、矩形，且所拼成图形的顶点均落在格点上，请在下面的菱形斜网格中画出示意图（每部分图注明①、②）。
19（8分）如图是某校甲班学生外出去基地参观，乘车、行步、骑车的人数分布直方图和扇形统计图。
（1）根据统计图求甲班步行的人数；
（2）甲班步行的对象根据步行人数通过全班随机抽号来确定；乙班学生去基地分两段路走，即学校——A地——基地，每段路走法有乘车或步行或骑车，你认为哪个班的学生有步行的可能性少？
（利用列表法或树状图求概率说明）。
人数
乘车
步行
骑车
20
12
乘车50％
步行
20％
骑车
30％
20（8分）如图，现有一横截面是一抛物线的水渠.水渠管理员将一根长1.5的标杆一端放在水渠底部的A点，另一端露出水面并靠在水渠边缘的B点，发现标杆有1浸没在水中，露出水面部分的标杆与水面成30°的夹角（标杆与抛物线的横截面在同一平面内）.
⑴以水面所在直线为轴，建立如图所示的直角坐标系，求该水渠横截面抛物线的解析式；
⑵在⑴的条件下，求当水面再上升0.3时的水面宽约为多少？(取2.2,结果精确到0.1).
A
B
30°

21（8分）如图，CE是⊙O的直径，BD切⊙O于点D，DE∥BO，CE的延长线交BD于点A。
（1）求证：直线BC是⊙O的切线；
（2）若AE=2，tan∠DEO=，求AD的长。
22（8分）为了增强居民节水意识，某市自来水公司对居民用水采用
以户为单位分段计费办法收费．即一月用水10吨以内（包括10吨）
的用户，每吨收水费元；一月用水超过10吨的用户，10吨水仍按每吨元收费，超过10吨的部分，按每吨元（）收费．设一户居民月用水吨，应收水费元，与之间的函数关系如图所示．
（1）求的值；某户居民上月用水8吨，应收水费多少元？
（2）求的值，并写出当时，与之间的函数关系式；
（3）已知居民甲上月比居民乙多用水4吨，两家共收水费46元，求他们上月各用水多少吨？

23（10分） 在直角坐标系中，点A的坐标为（6，0），B是x轴上不与点O、A 重合的一动点，设其横坐标为t（t为不等于0和6的整数），分别以OB、AB为一 边在x轴上方作等边△OBC和等边△BAD，连CD，以CD为边在△OBC、 △BAD的异侧作等边△CDP，记B的坐标为（t，0）时，对应P的纵坐标为ht，如B的坐标为（－2，0）时，对应P的纵坐标记为h－2.
（1）特例体验
如图（1），当t＝7时，求P的纵坐标h7的值；经过求h7的值，则画图（2）可得
h－1＝ ；
（2）探究结论
通过（1）的计算，归纳探索可得 h8＝h－2＝ ， ht＝h－t＋6＝ （用t表示）；
（3）拓宽应用
①通过（1）（2）探究发现，P的纵坐标与某个等边三角形的高有关，当t＝1、2、3、4、5时，利用图（3）可构造一个等边三角形，并求h1＋h2＋h3＋h4＋h5的值；
O
A
B
D
C
P
y
x
P
D
C
A
O
B
（图3）
x
y
②由此可知，如h1＋h2＋h3＋……＋ht＋h－1＋h－2＋……＋h－t+6=（2025×1006+15） 则t＝ 。
y
P
C
D

x
B
A
O
（图1）
（图2）
24（12分）、如图，平面直角坐标系中，A（0, 4），C（4, 0），D是OC中点，E是直线AD上的一动点，以OE为边作正方形OFGE（逆时针标记），连FC交AE于H。
（1）当D与E重合时，求直线FC解析式；
（2）当正方形OFGE面积最小时，求过O、F、C抛物线的解析式；
x
y
A
O
C
F
E
H
G
D
（3）设E的横坐标为t，如△HFE与△OAD相似，请直接求出t的值
中考数学第一次模拟试卷（4）参考答案
一、选择题
B、C、A、D、D、A、D、B、B、A、B、C
二、填空题
11、9.46×1012 12、2x（不唯一） 13、4.5 14、7
15、π或3π 16、（3，4）
三、解答题
17、（1） ； （2）x＝0。 （每小题3分）
18、图略（每图2分）
19、（1）8人（2分） （2）P（甲）＝ （2分） P（乙）＝（2分），
甲班（图略）（2分）
20、（1） B（，）（1分） y＝x2－（3分）
（2） x＝≈1.3（m）， 答：水面宽2.6米（4分）
21、（1）证明略（4分）
（2） AD＝2（4分）
22、（1）． （1分）
用8吨水应收水费（元）． （1分）
（2） ． 得．． （2分）
当时，． （ 1分）
（3）因，
所以甲、乙两家上月用水均超过10吨． （1分）
设甲、乙两家上月用水分别为吨，吨，
则 解之，得 答略 （2分）
23、（1）h7＝（2分） h－1＝（1分）
（2） h8＝h－2＝４（2分） ht＝h－t＋6＝ （１分）
（３）证△BCD≌△FDP≌△EPC，得等边△BEF边长为6（1分）
h1＋h2＋h3＋h4＋h5＝5×3＝15（1分）
t＝2018 （2分）

24、（1）F（0，－2），（1分） y＝x－2（3分）
（2） F（，－）（1分） y＝x2－x（3分）
（3） －2t＋4＝－t t1＝4 t＝4－2t t2＝
2（－4＋2t）＝－＋2t－4 t3＝－
2（－2t＋4＋）＝－4＋2t t4＝ （每个1分）
中考数学第一次模拟试卷（5）
一、选择题(本大题共10个小题，每小题3分，共30分)
1、的倒数是（ ）
A、 B、 C、 D、
2、下列图形是我国国产品牌汽车的标识，在这些汽车标识中，既不是中心对称图形也不
是轴对称图形的是（ ）
3、若一个圆锥的侧面积是18π，侧面展开图是半圆，则该圆锥的底面圆半径是（ ）
A、6 B、3 C、 D、12
4、如图，把三角板的直角顶点放在直尺的一边上，若∠1=27°，则∠2的度数是（ ）
A、53°B、63°C、73°D、27°
第5题图 第6题图
5、对于任意的实数m，一元二次方程3x2－x=的根的情况是（ ）
A、有两个相等的实数根 B、对于不同的实数m，方程根的情况也不相同
C、有两个不相等的实数根 D、无实数根
6、如图，Rt△ABC中，∠ACB=90°，AC=4cm，BC=6cm，以斜边AB上的一点O为
心所作的半圆分别与AC、BC相切于点D、E，则圆O的半径为（ ）
A、3. 5cm B、 2. 5cm C、2cm D、2. 4cm
7、已知一元二次方程x2－3x－1=0的两个根分别是x1、x2，则x12x2+x1x22的值为（ ）
A、－3 B、3 C、－6 D、6
8、如图，AC是矩形ABCD的对角线，AB=1，BC＝，点E，F分别是线段AB，AD上
的点，连接CE，CF，若∠BCE=∠ACF，且CE=CF，则AE+AF＝（ ）
A、1.2 B、 C、 D、
9、矩形ABCD中，AD=8cm，AB=6cm，动点E从点C开始沿边CB向点B以2cm/s的速度运动，动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止。如图可得到矩形CFHE，设运动时间为x(单位：s)，此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位：cm2)，则y与x之间的函数关系用图象表示大致是下图中的（ ）
10、将一副三角尺(在Rt△ACB中，∠ACB=90°，∠B=60°；在Rt△EDF中，∠EDF＝90°，∠E=45°)如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C。将△EDF绕点D顺时针方向旋转角α(0°