人教版七年级下册7.1.2平面直角坐标系当堂检测题

这是一份人教版七年级下册7.1.2平面直角坐标系当堂检测题，文件包含必刷基础题71-72平面直角坐标系坐标方法的简单应用原卷版-2023-2024学年七年级数学下册同步必刷题闯关练人教版docx、必刷基础题71-72平面直角坐标系坐标方法的简单应用解析版-2023-2024学年七年级数学下册同步必刷题闯关练人教版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
7.1-7.2 平面直角坐标系坐标方法的简单应用
知识点1：点的坐标
【典例分析01】（2021春•饶平县校级期末）如图，在平面直角坐标系xOy中，点A（3，0），判断在M，N，P，Q四点中，满足到点O和点A的距离都小于2的点是 ．
【思路引导】分别以点O和点A为圆心，2为半径画圆，即可得到满足到点O和点A的距离都小于2的点．
【完整解答】解：如图，分别以点O和点A为圆心，2为半径画圆，
可得满足到点O和点A的距离都小于2的点是点M与点N，
故答案为：点M与点N．
【变式训练01】（2021秋•沂源县期末）在平面直角坐标系中，下列各点在第二象限的是（ ）
A．（﹣2，﹣1）B．（2，1）C．（2，﹣1）D．（﹣2，1）
【变式训练02】（2021秋•丹东期末）在平面直角坐标系中，点M（m﹣3，m+1）在x轴上，则点M的坐标为（ ）
A．（﹣4，0）B．（0，﹣2）C．（﹣2，0）D．（0，﹣4）
【变式训练03】（2021春•鼓楼区校级期中）若在平面直角坐标系中，点P的坐标是（x，y）且x＞y，则点P不可能在第 象限．
【变式训练04】（2021春•饶平县校级期末）已知点P（2x，3x﹣1）是平面直角坐标系内的点．
（1）若点P在第一象限的角平分线上，求x的值；
（2）若点P在第三象限，且到两坐标轴的距离之和为16，求x的值．
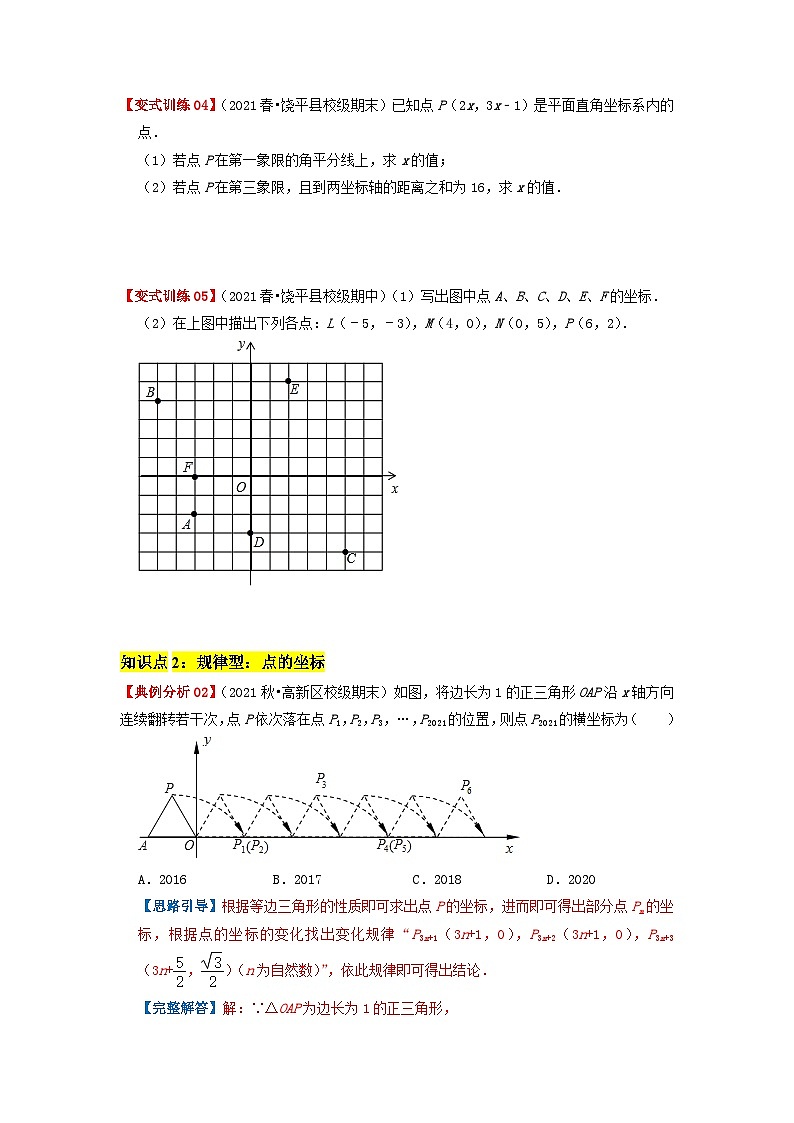
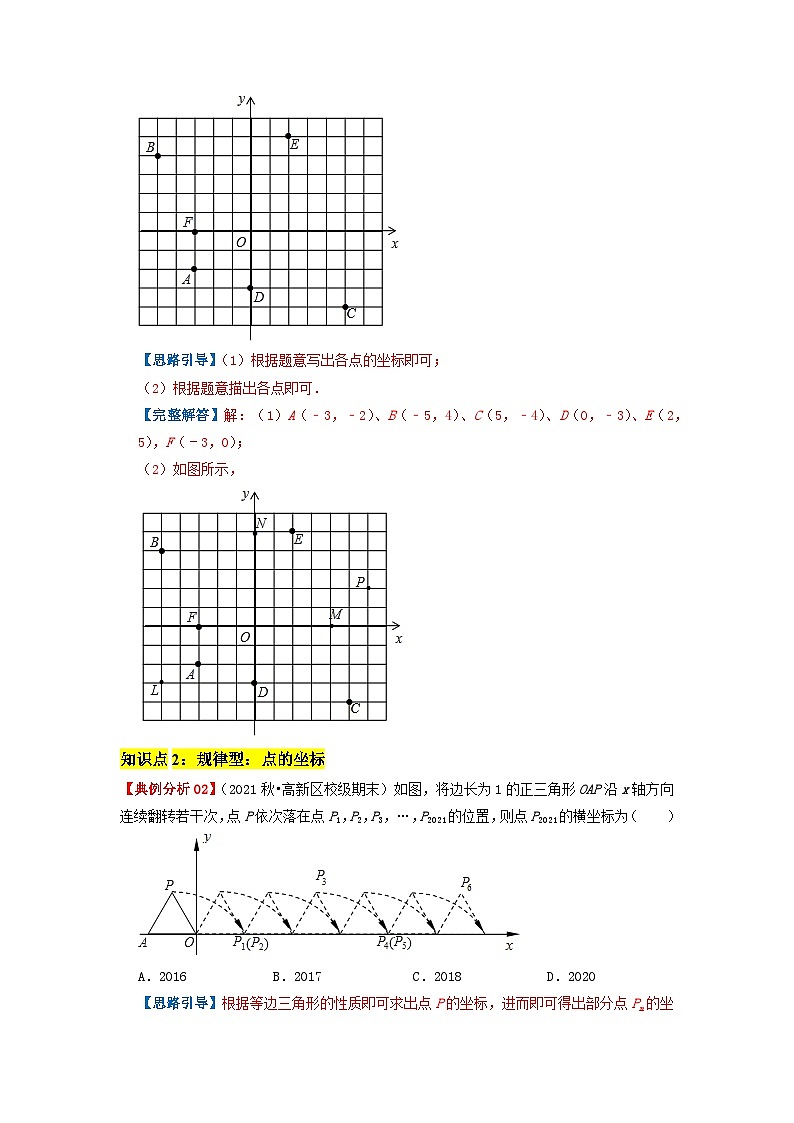
【变式训练05】（2021春•饶平县校级期中）（1）写出图中点A、B、C、D、E、F的坐标．
（2）在上图中描出下列各点：L（﹣5，﹣3），M（4，0），N（0，5），P（6，2）．
知识点2：规律型：点的坐标
【典例分析02】（2021秋•高新区校级期末）如图，将边长为1的正三角形OAP沿x轴方向连续翻转若干次，点P依次落在点P1，P2，P3，…，P2021的位置，则点P2021的横坐标为（ ）
A．2016B．2017C．2018D．2020
【思路引导】根据等边三角形的性质即可求出点P的坐标，进而即可得出部分点Pn的坐标，根据点的坐标的变化找出变化规律“P3n+1（3n+1，0），P3n+2（3n+1，0），P3n+3（3n+，）（n为自然数）”，依此规律即可得出结论．
【完整解答】解：∵△OAP为边长为1的正三角形，
∴点P的坐标为（﹣，）．
观察，发现：P1（1，0），P2（1，0），P3（，），P4（4，0），P5（4，0），P6（，），P7（7，0），…，
∴P3n+1（3n+1，0），P3n+2（3n+1，0），P3n+3（3n+，）（n为自然数）．
∵2021＝673×3+2，
∴点P2021的坐标为（2020，0）．
故选：D．
【变式训练06】（2021秋•管城区校级期末）如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，是斜边在x轴上，斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，﹣1），A3（0，0），则依图中所示规律，A2021的横坐标为（ ）
A．﹣1008B．﹣1010C．1012D．﹣1012
【变式训练07】（2021秋•河口区期末）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2）…按这样的运动规律经过第2021次运动后，动点P的坐标是 ．
【变式训练08】（2021秋•芗城区校级期中）如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一条长为2025个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A﹣的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是
【变式训练09】（2021春•岚山区期末）已知整点（横纵坐标都是整数）P0在平面直角坐标系内做“跳马运动”（即中国象棋“日”字型跳跃）．例如在图1中，从点A做一次“跳马运动”，可以到点B，也可以到达点C．设P0做一次跳马运动到点P1，做第二次跳马运动到点P2，做第三次跳马运动到点P3，…，如此依次进行．
（1）若P0（1，0），则P1可能是下列的点 ．
D（﹣1，2）；E（﹣2，0）；F（0，2）．
（2）已知点P0（4，2），P2（1，3），则点P1的所有可能坐标为 ；
（3）若P0（0，0），则P12、P13可能与P0重合的是 ．
（4）如图2，点P0（1，0）沿x轴正方向向右上方做跳马运动，若P跳到Q1位置，称为做一次“正横跳马”；若P跳到Q2位置，称为做一次“正竖跳马”．当点P连续做了a次“正横跳马”和b次“正竖跳马”后，到达点Pn（14，11），求a+b的值．
【变式训练10】（2021春•自贡期末）综合与实践
问题背景：
（1）已知A（1，2），B（3，2），C（1，﹣1），D（﹣3，﹣3）．在平面直角坐标系中描出这几个点，并分别找到线段AB和CD中点P1、P2，然后写出它们的坐标，则P1 ，P2 ．
探究发现：
（2）结合上述计算结果，你能发现若线段的两个端点的坐标分别为（x1，y1），（x2，y2），则线段的中点坐标为 ．
拓展应用：
（3）利用上述规律解决下列问题：已知三点E（﹣1，2），F（3，1），G（1，4），第四个点H（x，y）与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．
知识点3：坐标确定位置
【典例分析03】（2021秋•前郭县期末）如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）A→C（ ， ），B→C（ ， ），
C→D （ ， ）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的最少路程；
（3）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置．
【变式训练11】（2021秋•高新区校级期末）如图所示的是一所学校的平面示意图，若用（2，3）表示教学楼的位置，（3，1）表示旗杆的位置，则实验楼的位置可表示成（ ）
A．（2，﹣3）B．（﹣3，2）C．（﹣2，1）D．（1，﹣2）
【变式训练12】（2021秋•招远市期末）如图，已知“车”的坐标为（﹣2，2），“马”的坐标为（1，2），则“炮”的坐标为（ ）
A．（3，0）B．（3，1）C．（3，2）D．（3，7）
【变式训练13】（2021•甘肃模拟）如图是莫高窟景区游览路线图的一部分，在图中建立平面直角坐标系，若表示敦煌研究院院史陈列馆的点的坐标为（﹣3，0），表示九层楼的点的坐标为（0，1），则表示美术馆的点的坐标为 ．
【变式训练14】（2021•山西）如图是一片枫叶标本，其形状呈“掌状五裂型”，裂片具有少数突出的齿，将其放在平面直角坐标系中，表示叶片“顶部”A，B两点的坐标分别为（﹣2，2），（﹣3，0），则叶杆“底部”点C的坐标为 ．
【变式训练15】（2021春•许昌期末）春天到了，某班同学组织到公园春游，如图是公园的平面图（小正方形的边长代表100m长），图中牡丹园的坐标是（300，300），望春亭的坐标为（﹣200，﹣100），请在图中建立平面直角坐标系并写出其它地点的坐标．
知识点4：坐标与图形性质
【典例分析04】（2021秋•锡山区期末）在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫做整点．已知点A（0，4），点B是x轴正半轴上的点，且点B的横坐标为n（n为正整数），记△AOB内部（不包括边界）的整点个数为m．
当n＝12时，m的值为 ；当n＝2022时，m的值为 ．
【变式训练16】（2021秋•新昌县期末）在平面直角坐标系中，点A的坐标为（﹣1，3），点B的坐标为（4，3），则线段AB上任意一点的坐标可表示为（ ）
A．（x，3）（﹣1≤x≤4）B．（x，3）（x≤4）
C．（x，3）（x≥﹣1）D．（x，3）
【变式训练17】．（2021秋•法库县期末）如图，在平面直角坐标系中，△ABC顶点A，B的坐标分别是（0，4），（0，﹣2），BC＝AC＝5，则顶点C的坐标为（ ）
A．（4，1）B．（1，4）C．（4，2）D．（3，1）
【变式训练18】（2021春•东城区期末）在平面直角坐标系xOy中，已知点A（a，﹣1），B（2，3﹣b），C（﹣5，4）．若AB∥x轴，AC∥y轴，则a+b＝ ．
【变式训练19】（2021秋•连城县期中）如图，平面直角坐标系xOy中，已知点A（0，3），点B（，0），连接AB则可量出∠OAB＝30°．若对于平面内一点C，当△ABC是以AB为腰的等腰三角形时，称点C是线段AB的“等长点”．
（1）在点，点，点中，线段AB的“等长点”是点
（2）若点D（m，n）是线段AB的“等长点”，且∠DAB＝60°，求m和n的值．
【变式训练20】（2021秋•北流市校级月考）如图，已知P（2m+5，3m+6）在第一象限角平分线上，点A，B分别在x轴正半轴和y轴正半轴上，∠BPA＝90°．
（1）求点P的坐标；
（2）若点B为（0，2），求点A的坐标．
知识点5：两点间的距离公式
【典例分析05】（2021•安徽模拟）先阅读下列一段文字，在回答后面的问题．
已知在平面内两点P1（x1，y1）、P2（x2，y2），其两点间的距离公式，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．
（1）已知A（2，4）、B（﹣3，﹣8），试求A、B两点间的距离；
（2）已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A、B两点间的距离．
（3）已知一个三角形各顶点坐标为A（0，6）、B（﹣3，2）、C（3，2），你能判定此三角形的形状吗？说明理由．
【思路引导】（1）根据两点间的距离公式来求A、B两点间的距离；
（2）根据两点间的距离公式|y2﹣y1|来求A、B两点间的距离．
（3）先将A、B、C三点置于平面直角坐标系中，然后根据两点间的距离公式分别求得AB、BC、AC的长度；最后根据三角形的三条边长来判断该三角形的形状．
【完整解答】解：（1）∵A（2，4）、B（﹣3，﹣8），
∴|AB|＝＝13，即A、B两点间的距离是13；
（2）∵A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，
∴|AB|＝|﹣1﹣5|＝6，即A、B两点间的距离是6；
（3）△ABC是等腰三角形，理由如下：
∵一个三角形各顶点坐标为A（0，6）、B（﹣3，2）、C（3，2），
∴AB＝5，BC＝6，AC＝5，
∴AB＝AC，
∴△ABC是等腰三角形．
【变式训练21】（2019秋•招远市期末）已知A，B两点的坐标是A（5，a），B（b，4），若AB平行于x轴，且AB＝3，则a+b的值为（ ）
A．﹣1B．9C．12D．6或12
【变式训练22】（2020春•赣州期末）在平面直角坐标系中，点A（﹣3，2），B（3，5），C（x，y），若AC∥x轴，则线段BC的最小值及此时点C的坐标分别为（ ）
A．6，（﹣3，5）B．10，（3，﹣5）C．1，（3，4）D．3，（3，2）
【变式训练23】（2021春•海淀区校级期末）A（0，a），B（3，5）是平面直角坐标系中的两点，线段AB长度的最小值为 ．
【变式训练24】（2020春•临河区期末）在平面直角坐标系中，若点M（2，4）与点N（x，4）之间的距离是3，则x的值是 ．
【变式训练25】（2018春•遵义期中）如图：在平面直角坐标系中有两点A（﹣5，0），B（0，4），求A，B两点的距离．
知识点6：坐标与图形变化-平移
【典例分析06】（2021秋•靖西市期中）如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）．
（1）画出三角形ABC，并求其面积；
（2）如图，△A′B′C′是由△ABC经过 ， 平移得到的．
（3）已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标是（ ， ）．
【思路引导】（1）根据点的位置作出图形，利用分割法求出三角形的面积即可；
（2）结合图象，利用平移变换的性质解决问题；
（3）利用平移变换的规律解决问题．
【完整解答】解：（1）如图，△ABC即为所求，S△ABC＝4×5﹣×2×4﹣×2×5﹣×3×2＝8；
（2）△ABC向右平移4个单位，再向下平移3个单位得到△A′B′C′，
故答案为：△ABC向右平移4个单位，再向下平移3个单位得到△A′B′C′，
（3）P′（a+4，b﹣3），
故答案为：a+4，b﹣3．
【变式训练26】（2021秋•海曙区期末）在平面直角坐标系中，将点P（﹣1，﹣4）向右平移3个单位长度后得到的点所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【变式训练27】（2021秋•桓台县期末）△ABC的顶点分别位于正方形网格的格点上，建立如图所示的平面直角坐标系，已知点C（﹣1，1），将△ABC先沿x轴方向向右平移3个单位长度，再沿y轴方向向下平移2个单位长度，得到△A′B′C′，则点A的对应点A′的坐标是（ ）
A．（﹣6，6）B．（0，2）C．（0，6）D．（﹣6，2）
【变式训练28】（2021秋•东营期末）如图，在平面直角坐标系中，设一质点M自P0（1，0）处向上运动1个单位P1（1，1），然后向左运动2个单位至P2处，再向下运动3个单位至P3处，再向右运动4个单位至P4处，再向上运动5个单位至P5处，…，如此继续运动下去，则P2022的坐标为 ．
【变式训练29】（2021春•孝南区月考）若将点P（2﹣m，2）向右平移3个单位长度后落在y轴上，则实数m＝ ．
【变式训练30】（2021秋•阜阳月考）在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），则称点Q是点P的“a阶派生
点”（其中a为常数，且a≠0）．例如：点P（1，4）的“2阶派生点”为点Q（2×1+4，1+2×4），即点Q（6，9）．
（1）若点P的坐标为（﹣1，5），则它的“3阶派生点”的坐标为 ；
（2）若点P的“5阶派生点”的坐标为（﹣9，3），求点P的坐标；
（3）若点P（c+1，2c﹣1）先向左平移2个单位长度，再向上平移1个单位长度后得到了点P1，点P1的“﹣3阶派生点”P2位于坐标轴上，求点P2的坐标．