第02讲 一般三角形及其性质（考点精析+真题精讲）-备战2024年中考数学一轮复习考点研究（全国通用）

这是一份第02讲 一般三角形及其性质（考点精析+真题精讲）-备战2024年中考数学一轮复习考点研究（全国通用），文件包含第二讲一般三角形及其性质考点精析+真题精讲原卷版docx、第二讲一般三角形及其性质考点精析+真题精讲解析版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
备战2024中考数学一轮复习
第2讲一般三角形及其性质
№考向解读
➊考点精析
➋真题精讲
➌题型突破
➍专题精练
第四章三角形
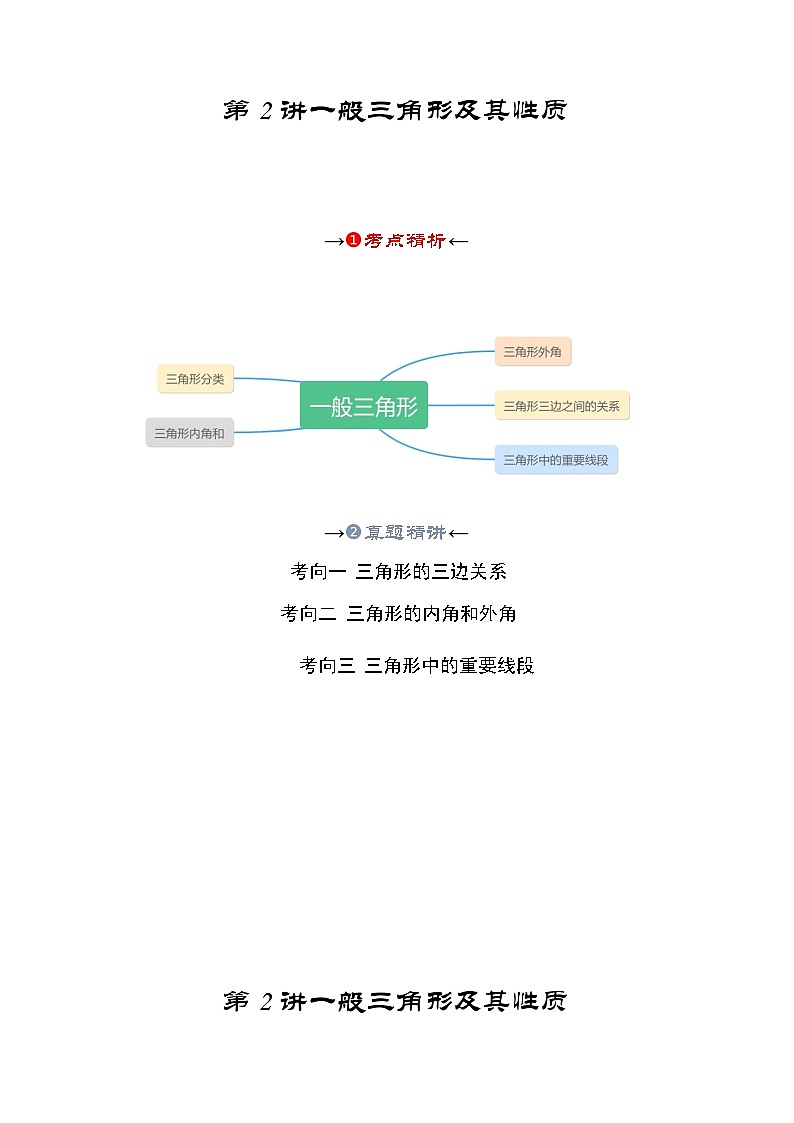
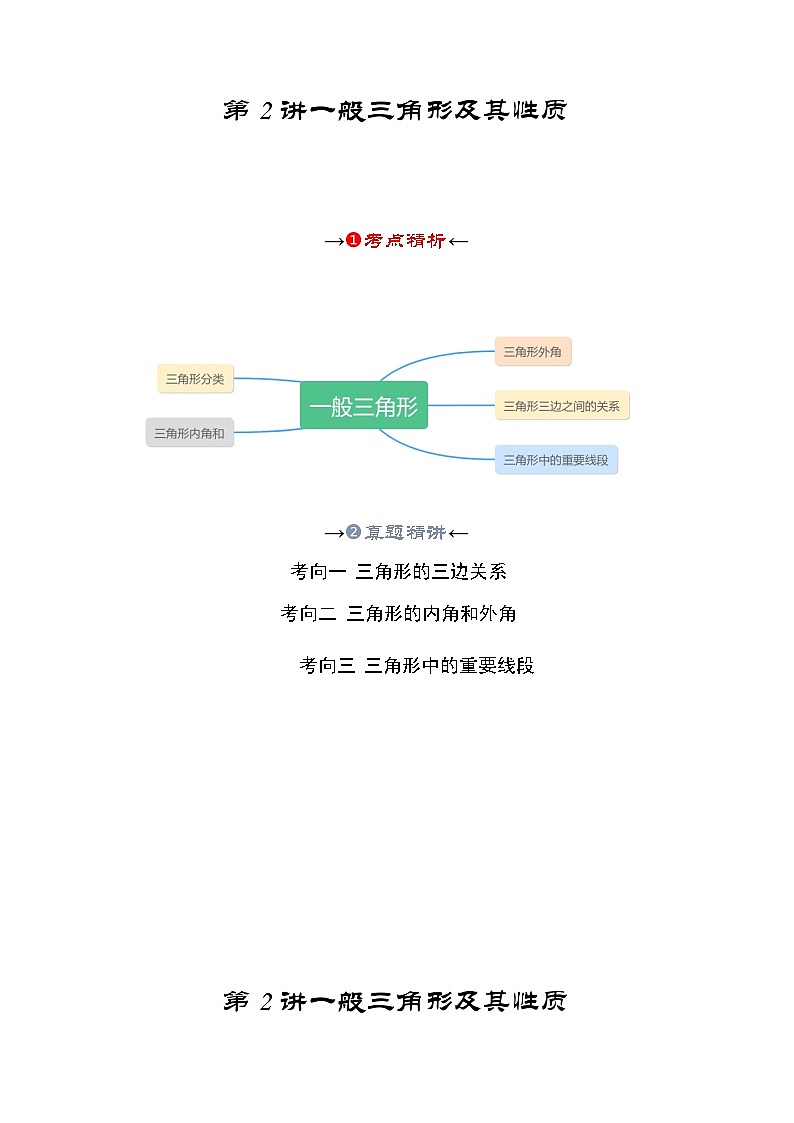
第2讲一般三角形及其性质
→➊考点精析←
→➋真题精讲←
考向一 三角形的三边关系
考向二 三角形的内角和外角
考向三 三角形中的重要线段
第2讲一般三角形及其性质
→➊考点精析←
一、三角形的基础知识
1．三角形的概念
由三条线段首尾顺次相接组成的图形，叫做三角形．
2．三角形的三边关系
（1）三角形三边关系定理：三角形的两边之和大于第三边．
推论：三角形的两边之差小于第三边．
（2）三角形三边关系定理及推论的作用：
①判断三条已知线段能否组成三角形；②当已知两边时，可确定第三边的范围；③证明线段不等关系．
3．三角形的内角和定理及推论
三角形的内角和定理：三角形三个内角和等于180°．
推论：①直角三角形的两个锐角互余；②三角形的一个外角等于和它不相邻的两个内角的和；③三角形的一个外角大于任何一个和它不相邻的内角．
4．三角形中的重要线段
（1）三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线．
（2）在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线．
（3）从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）．
（4）连接三角形两边中点的线段叫做三角形的中位线，三角形的中位线平行于第三边，且等于第三边的一半．
→➋真题精讲←
考向一 三角形的三边关系
1．（2023·湖南·统考中考真题）下列长度的各组线段能组成一个三角形的是（ ）
A．B．
C．D．
2．（2021·湖南岳阳市·中考真题）下列命题是真命题的是（ ）
A．五边形的内角和是B．三角形的任意两边之和大于第三边
C．内错角相等D．三角形的重心是这个三角形的三条角平分线的交点
3.小芳有两根长度为6 cm和9 cm的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为__________的木条．
A．2 cmB．3 cm
C．12 cmD．15 cm
4．（2023·江苏连云港·统考中考真题）一个三角形的两边长分别是3和5，则第三边长可以是__________．（只填一个即可）
考向二 三角形的内角和外角
5．（2023·四川眉山·统考中考真题）如图，中，，则的度数为（ ）

A．B．C．D．
6．（2021·安徽中考真题）两个直角三角板如图摆放，其中，，，AB与DF交于点M．若，则的大小为（ ）
A．B．C．D．
7.小桐把一副直角三角尺按如图所示的方式摆放在一起，其中，，，，则等于
A．B．C．D．
8．（2023·四川宜宾·统考中考真题）如图， ，且，，则等于（ ）

A．B．C．D．
9．（2021·陕西中考真题）如图，点D、E分别在线段、上，连接、．若，，，则的大小为（ ）
A．60°B．70°C．75°D．85°
10．（2023·新疆·统考中考真题）如图，在中，若，，，则______．

11．（2021·江苏苏州市·中考真题）如图．在中，，．若，则______．
考向三 三角形中的重要线段
12．（2023·云南·统考中考真题）如图，两点被池塘隔开，三点不共线．设的中点分别为．若米，则（ ）

A．4米B．6米C．8米D．10米
13．（2023·安徽·统考中考真题）清初数学家梅文鼎在著作《平三角举要》中，对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明，证明过程中创造性地设计直角三角形，得出了一个结论：如图，是锐角的高，则．当，时，____．