第02讲 一般三角形及其性质（题型突破+专题精练）-备战2024年中考数学一轮复习考点研究（全国通用）

这是一份第02讲 一般三角形及其性质（题型突破+专题精练）-备战2024年中考数学一轮复习考点研究（全国通用），文件包含第二讲一般三角形及其性质题型突破+专题精练原卷版docx、第二讲一般三角形及其性质题型突破+专题精练解析版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
→➌题型突破←→➍专题训练←
题型一 三角形的三边关系
1.长度分别为2，3，3，4的四根细木棒首尾相连，围成一个三角形（木棒允许连接，但不允许折断），得到的三角形的最长边长为（ ）
A．4B．5C．6D．7
【答案】B
【解析】
【分析】
利用三角形的三边关系列举出所围成三角形的不同情况，通过比较得到结论.
【详解】
①长度分别为5、3、4，能构成三角形，且最长边为5；
②长度分别为2、6、4，不能构成三角形；
③长度分别为2、7、3，不能构成三角形；
④长度分别为6、3、3，不能构成三角形；
综上所述，得到三角形的最长边长为5．
故选：B.
【点睛】
此题考查构成三角形的条件，三角形的三边关系，解题中运用不同情形进行讨论的方法，注意避免遗漏构成的情况.
题型二 三角形的内角和外角
2.如图，直线，且于点，若，则的度数为（ ）
A．65°B．55°C．45°D．35°
【答案】B
【解析】
【分析】
根据三角形的内角和求得，再根据平行线的性质可得到的度数．
【详解】
解：∵，，
∴，
∵，
∴，
故选：B．
【点睛】
本题考查三角形的内角和、平行线的性质，熟练运用平行线的性质定理是解题的关键．
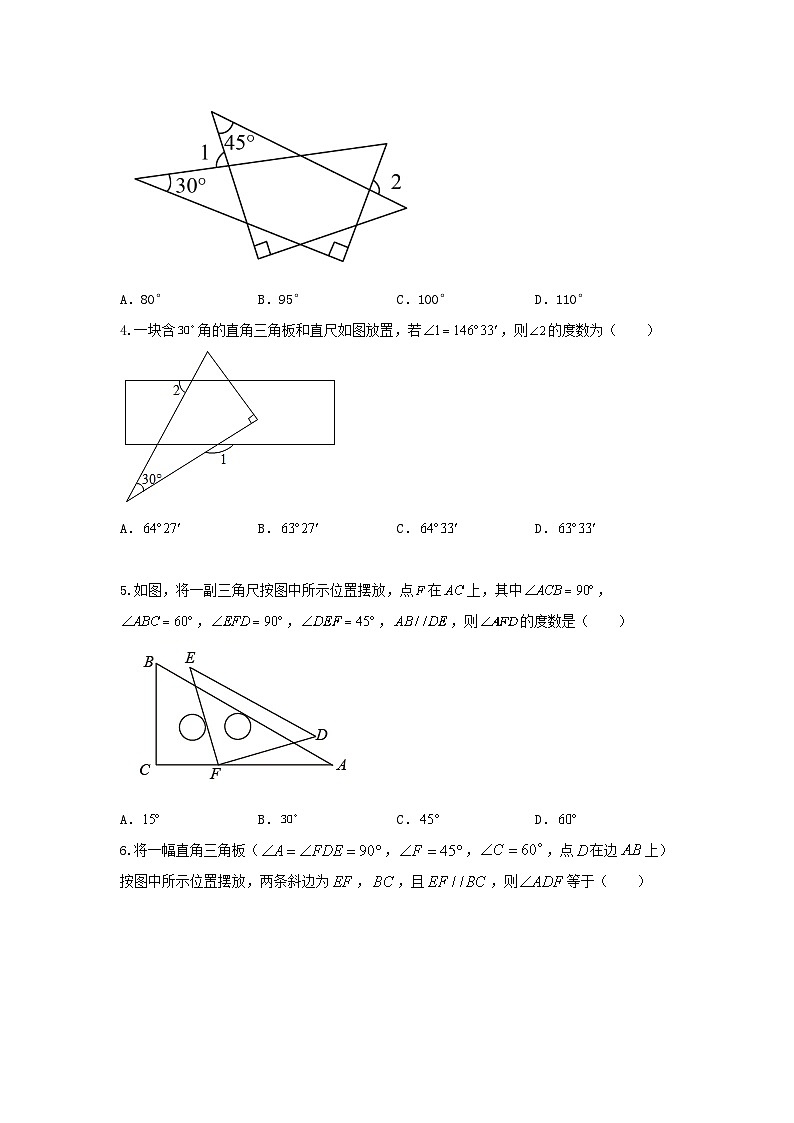
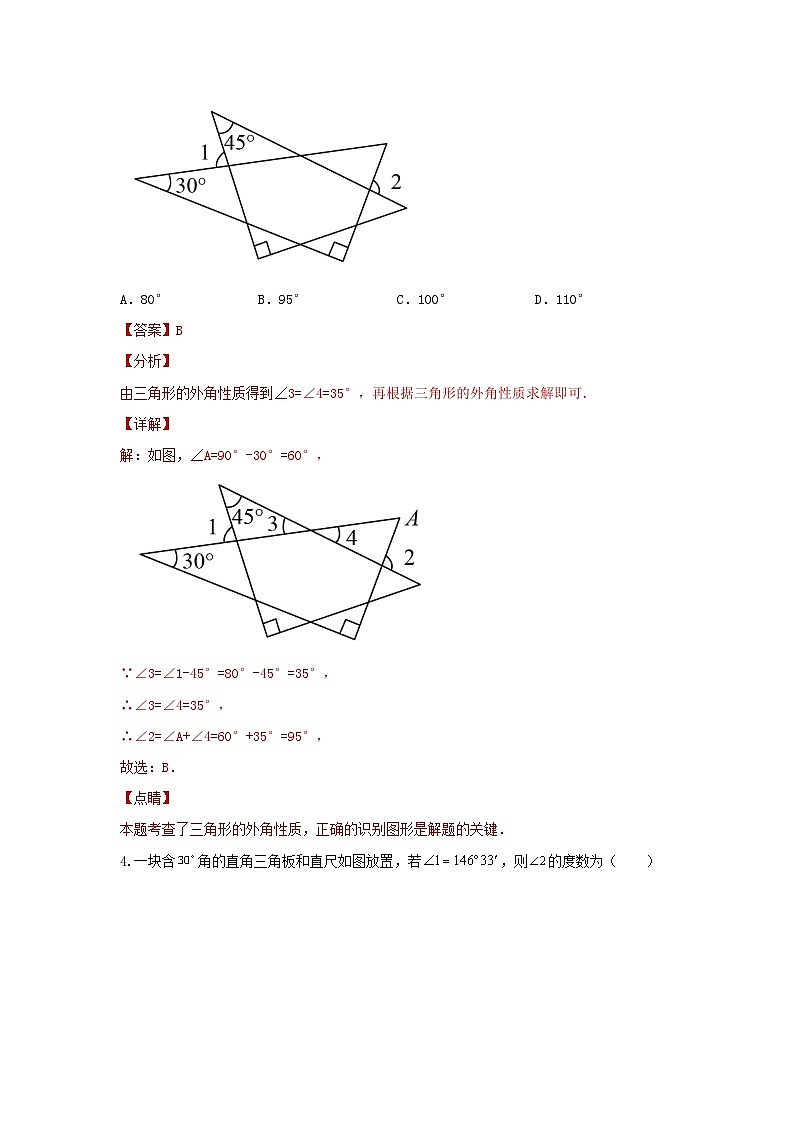
3.一副三角板如图所示摆放，若，则的度数是（ ）
A．80°B．95°C．100°D．110°
【答案】B
【分析】
由三角形的外角性质得到∠3=∠4=35°，再根据三角形的外角性质求解即可．
【详解】
解：如图，∠A=90°-30°=60°，
∵∠3=∠1-45°=80°-45°=35°，
∴∠3=∠4=35°，
∴∠2=∠A+∠4=60°+35°=95°，
故选：B．
【点睛】
本题考查了三角形的外角性质，正确的识别图形是解题的关键．
4.一块含角的直角三角板和直尺如图放置，若，则的度数为（ ）
A．B．C．D．
【答案】B
【分析】
先根据邻补角的定义得出∠3=180°-∠1=33°27′，再根据平行线的性质得到∠4=∠2，然后根据三角形的外角的性质即可得到结论．
【详解】
解：∵，
∴∠3=180°-∠1=33°27′，
∴∠4=∠3+30°=63°27′，∵AB∥CD，
∴∠2=∠4=63°27′，
故选：B．
【点睛】
本题考查了平行线的性质，三角形外角性质的应用，能求出∠3的度数是解此题的关键，注意：两直线平行，内错角相等．
5.如图，将一副三角尺按图中所示位置摆放，点在上，其中，，，，，则的度数是（ ）
A．B．C．D．
【答案】A
【分析】
设AB与EF交于点M，根据，得到，再根据三角形的内角和定理求出结果．
【详解】
解：设AB与EF交于点M，
∵，
∴，
∵，，
∴，
∴,
∵,
∴=，
故选：A．
．
【点睛】
此题考查平行线的性质，三角形的内角和定理，熟记平行线的性质并应用是解题的关键．
6.将一幅直角三角板（，，，点在边上）按图中所示位置摆放，两条斜边为，，且，则等于（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
根据平行线的性质可得∠1=∠F=45°，再根据三角形内角与外角的关系可得∠1的度数．
【详解】
解：如图，
∵，
∴∠1=∠F=45°，
又∵，
∴∠B=30°，
∴，
故选：B．
【点睛】
此题主要考查了平行线的性质以及三角形外角性质的应用，关键是掌握两直线平行，同位角相等．
7.如图，已知直线和相交于点若，则等于（ ）
A．B．C．D．
【答案】C
【解析】
【分析】
先根据得到，再运用三角形内角和定理求出的度数即可．
【详解】
∵，
∴，
∵，
∴
∵，且，
∴，
故选：C．
【点睛】
此题主要考查了平行线的性质以及三角形内角和定理，熟练掌握性质和定理是解答此题的关键，比较简单．
8.如图，AB和CD相交于点O，则下列结论正确的是（ ）
A．∠1=∠2B．∠2=∠3C．∠1＞∠4+∠5D．∠2＜∠5
【答案】A
【解析】
【分析】
根据对顶角性质、三角形外角性质分别进行判断，即可得到答案．
【详解】
解：由两直线相交，对顶角相等可知A正确；
由三角形的一个外角等于它不相邻的两个内角的和可知
B选项为∠2＞∠3，
C选项为∠1=∠4+∠5，
D选项为∠2＞∠5．
故选：A．
【点睛】
本题考查了三角形的外角性质，对顶角性质，解题的关键是熟练掌握三角形的外角性质进行判断．
9.如图摆放的一副学生用直角三角板，，与相交于点G，当时，的度数是（ ）
A．135°B．120°C．115°D．105°
【答案】D
【解析】
【分析】
过点G作，则有，，又因为和都是特殊直角三角形，，可以得到，有即可得出答案．
【详解】
解：过点G作，有，
∵在和中，
∴
∴，
∴
故的度数是105°．
【点睛】
本题主要考查了平行线的性质和三角形内角和定理，其中平行线的性质为：两直线平行，内错角相等；三角形内角和定理为：三角形的内角和为180°；其中正确作出辅助线是解本题的关键．
10.如图，是的外角，若，，则（ ）
A．B．C．D．
【答案】D
【解析】
【分析】
根据三角形的外角的性质进行计算即可．
【详解】
解：∵是的外角，
∴=∠B+∠A
∴∠A=-∠B，
∴∠A=60°
故选：D
【点睛】
本题考查了三角形外角的性质，熟练掌握三角形外角的性质是解题的关键．
11.如图，a∥b，一块含45°的直角三角板的一个顶点落在其中一条直线上，若∠1＝65°，则∠2的度数为（ ）
A．25°B．35°C．55°D．65°
【分析】根据两直线平行，同位角相等可得∠3＝∠1，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠4，然后根据对顶角相等解答．
【解析】如图：
∵∠1＝65°，∠1+45°+∠3＝180°，
∴∠3＝180°﹣45°﹣65°＝70°，
∵a∥b，
∴∠4+∠2＝∠3＝70°，
∵∠4＝45°，
∴∠2＝70°﹣∠4＝70°﹣45°＝25°．
故选：A．
12.如图，，，垂足为E，若，则的度数为（ ）
A．40°B．50°C．60°D．90°
【答案】B
【分析】
由题意易得，，然后问题可求解．
【详解】
解：∵，，
∴，
∵，
∴，
∴；
故选B．
【点睛】
本题主要考查平行线的性质及直角三角形的两个锐角互余，熟练掌握平行线的性质及直角三角形的两个锐角互余是解题的关键．
13．如图，是的外角，．若，，则的度数为（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
根据平行线的性质及三角形的内角和定理即可求解．
【详解】
∵，
∴∠B=
∴∠A=180°-∠B-
故选B．
【点睛】
此题主要考查三角形的内角和，解题的关键是熟知三角形的内角和等于180°．
14.一副三角板如图所示摆放，且，则的度数为__________．
【答案】
【分析】
根据三角板的2个三角形中的特殊角求出即可．
【详解】
如图，
．
故答案为．
【点睛】
本题考查了平行线的性质，三角形的外角性质，利用三角形的外角来求的度数是解题的关键．
15.如图，在中，点D、E分别在、上，．若，则________．
【答案】100
【分析】
先根据三角形内角和定理求出∠A=80°，再根据平行线的性质，求出，即可．
【详解】
解：∵，
∴∠A=180°-40°-60°=80°，
∵，
∴180°-80°=100°．
故答案是100．
【点睛】
本题主要考查三角形内角和定理以及平行线的性质，掌握两直线平行，同旁内角互补，是解题的关键．
题型三 三角形中的重要线段
16.观察下列作图痕迹，所作CD为△ABC的边AB上的中线是（ ）
A．B．
C．D．
【答案】B
【解析】
【分析】
根据题意，CD为△ABC的边AB上的中线，就是作AB边的垂直平分线，交AB于点D，点D即为线段AB的中点，连接CD即可判断．
【详解】
解：作AB边的垂直平分线，交AB于点D，连接CD，
∴点D即为线段AB的中点，
∴CD为△ABC的边AB上的中线．
故选：B．
【点睛】
本题主要考查三角形一边的中线的作法；作该边的中垂线，找出该边的中点是解题关键．
17.如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝6，AC＝5，则△ACE的周长为（ ）
A．8B．11C．16D．17
【分析】在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝6，AC＝5，则△ACE的周长为
【解析】∵DE垂直平分AB，
∴AE＝BE，
∴△ACE的周长＝AC+CE+AE
＝AC+CE+BE
＝AC+BC
＝5+6
＝11．
故选：B．