第03讲 特殊三角形及其性质(含解直角三角形)（题型突破+专题精练）-备战2024年中考数学一轮复习考点研究（全国通用）

这是一份第03讲 特殊三角形及其性质(含解直角三角形)（题型突破+专题精练）-备战2024年中考数学一轮复习考点研究（全国通用），文件包含第三讲特殊三角形及其性质含解直角三角形题型突破+专题精练原卷版docx、第三讲特殊三角形及其性质含解直角三角形题型突破+专题精练解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
→➌题型突破←→➍专题训练←
题型一等腰三角形
1．如图，在△ABC中，AB＝AC，∠BAC＝108°，若AD、AE三等分∠BAC，则图中等腰三角形有（ ）
A．3个B．4个C．5个D．6个
【答案】D
【解析】解：∵AB＝AC，∠BAC＝108°，
∴∠B＝∠C＝36°，△ABC是等腰三角形，
∵∠BAC＝108°，AD、AE三等分∠BAC，
∴∠BAD＝∠DAE＝∠EAC＝36°，
∴∠DAC＝∠BAE＝72°，
∴∠AEB＝∠ADC＝72°，
∴BD＝AD＝AE＝CE，AB＝BE＝AC＝CD，
∴△ABE、△ADC、△ABD、△ADE、△AEC是等腰三角形，
∴一共有6个等腰三角形．
故选：D．
2．在△ABC中，∠BAC，∠ACB的平分线相交于I，DE过点I且DE∥AC，若AD＝3cm，CE＝5cm，则DE＝（ ）
A．8B．6C．7D．5
【答案】A
【解析】解：∵DE∥AC，
∴∠ACI＝∠CIE，
∵CI平分∠ACB，
∴∠ACI＝∠ECI，
∴∠ECI＝∠CIE，
∴EI＝CE＝5，
同理可得：DI＝AD＝3，
∴DE＝DI+EI＝5+3＝8；
故选：A．
3．在△ABC中，已知∠A＝∠B，且该三角形的一个内角等于100°．现有下面四个结论：①∠A＝100°；②∠C＝100°；③AC＝BC；④AB＝BC．其中正确结论的个数为（ ）
A．1个B．2个C．3个D．4个
【答案】B
【解析】解：
∠A＝∠B＝100°时，∠A+∠B+∠C＞180°，不符合三角形的内角和定理，∴①错误；
∠C＝100°时，∠A＝∠B＝（180°﹣∠C）＝40°，∴②正确；
∵∠A＝∠B，
∴AC＝BC，③正确；④错误；
正确的有②③，2个，
故选：B．
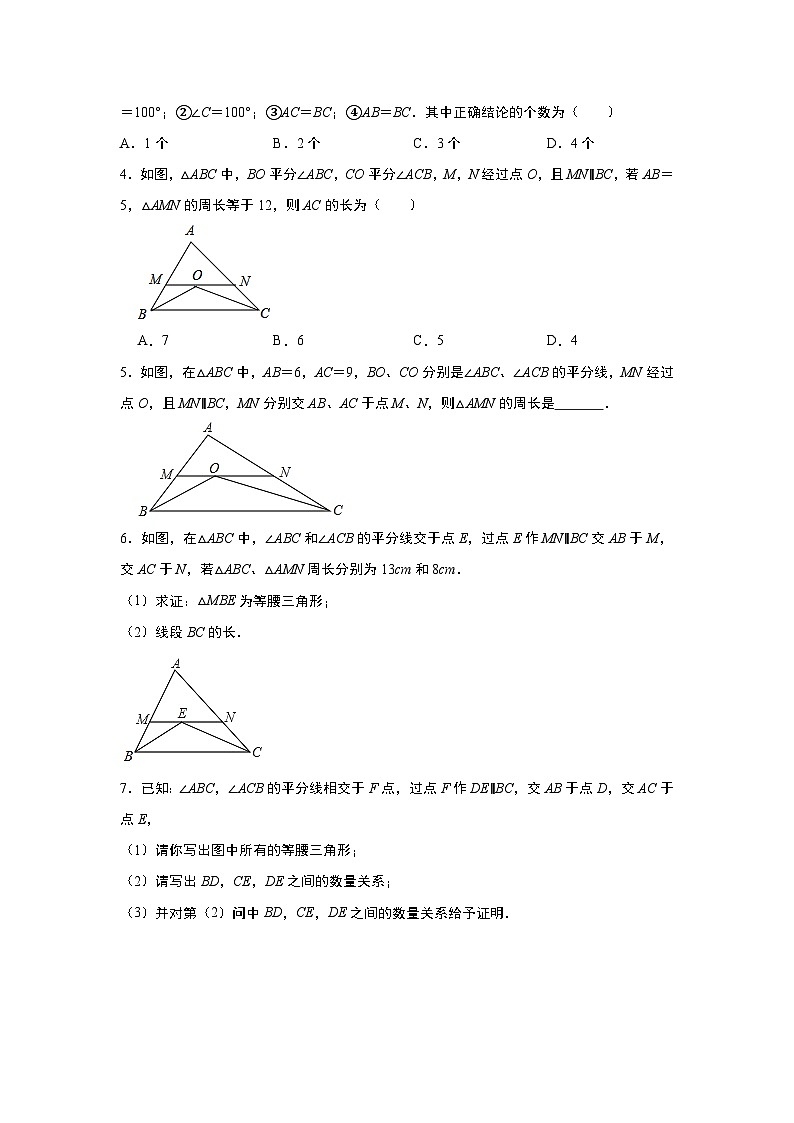
4．如图，△ABC中，BO平分∠ABC，CO平分∠ACB，M，N经过点O，且MN∥BC，若AB＝5，△AMN的周长等于12，则AC的长为（ ）
A．7B．6C．5D．4
【答案】A
【解析】解：∵BO平分∠CBA，CO平分∠ACB，
∴∠MBO＝∠OBC，∠OCN＝∠OCB，
∵MN∥BC，
∴∠MOB＝∠OBC，∠NOC＝∠OCB，
∴∠MBO＝∠MOB，∠NOC＝∠NCO，
∴MO＝MB，NO＝NC，
∵AB＝5，△AMN的周长等于12，
∴△AMN的周长＝AM+MN+AN＝AB+AC＝5+AC＝12，
∴AC＝7，
故选：A．
5．如图，在△ABC中，AB＝6，AC＝9，BO、CO分别是∠ABC、∠ACB的平分线，MN经过点O，且MN∥BC，MN分别交AB、AC于点M、N，则△AMN的周长是 ．
【答案】15
【解析】解：∵在△ABC中，∠BAC与∠ACB的平分线相交于点O，
∴∠ABO＝∠OBC，∠ACO＝∠BCO，
∵MN∥BC，
∴∠MOB＝∠OBC，∠NOC＝∠OCB，
∴∠ABO＝∠MOB，∠ACO＝∠NOC，
∴BM＝OM，CN＝ON，
∴△AMN的周长是：AM+NM+AN＝AM+OM+ON+AN＝AM+BM+CN+AN＝AB+AC＝9+6＝15．
故答案为：15．
6．如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若△ABC、△AMN周长分别为13cm和8cm．
（1）求证：△MBE为等腰三角形；
（2）线段BC的长．
【解析】解：如图所示：
（1）∵BE是∠ABC的角平分线，
∴∠1＝∠2，
又∵MN∥BC，
∴∠5＝∠2，
∴∠1＝∠5，
∴△MBE为等腰三角形；
（2）∵△MBE为等腰三角形，
∴MB＝ME，
同理可得：NE＝NC，
又∵l△AMN＝AM+AN+MN，
MN＝ME+NE，
∴l△AMN＝AM+AN+ME+NE＝AM+BM+AN+CN，
∴l△AMN＝AB+AC＝8．
又∵l△ABC＝AB+AC+BC＝13，
∴BC＝13﹣8＝5cm．
7．已知：∠ABC，∠ACB的平分线相交于F点，过点F作DE∥BC，交AB于点D，交AC于点E，
（1）请你写出图中所有的等腰三角形；
（2）请写出BD，CE，DE之间的数量关系；
（3）并对第（2）问中BD，CE，DE之间的数量关系给予证明．
【解析】
解：（1）等腰三角形有：△BDF和△CEF；
（2）BD+CE＝DE；
（3）∵BF平分∠ABC，
∴∠1＝∠2，
∵DE∥BC，
∴∠2＝∠3，
∴∠1＝∠3，
∴BD＝DF，
同理可得CE＝EF，
∴BD+CE＝DF+EF＝DE，
即BD+CE＝DE．
8．（1）如图1，已知：在△ABC中，AB＝AC＝10，BD平分∠ABC，CD平分∠ACB，过点D作EF∥BC，分别交AB、AC于E、F两点，则图中共有 个等腰三角形；EF与BE、CF之间的数量关系是 ，△AEF的周长是
（2）如图2，若将（1）中“△ABC中，AB＝AC＝10”改为“若△ABC为不等边三角形，AB＝8，AC＝10”其余条件不变，则图中共有 个等腰三角形；EF与BE、CF之间的数量关系是什么？证明你的结论，并求出△AEF的周长
（3）已知：如图3，D在△ABC外，AB＞AC，且BD平分∠ABC，CD平分△ABC的外角∠ACG，过点D作DE∥BC，分别交AB、AC于E、F两点，则EF与BE、CF之间又有何数量关系呢？直接写出结论不证明．
【解析】
解：（1）BE+CF＝EF．
理由如下：
∵AB＝AC，
∴∠ABC＝∠ACB，
∵BD平分∠ABC，CD平分∠ACB，
∴∠EBD＝∠CBD，∠FCD＝∠BCD，
∴∠DBC＝∠DCB，
∴DB＝DC
∵EF∥BC，
∴∠AEF＝∠ABC，∠AFE＝∠ACB，∠EDB＝∠CBD，∠FDC＝∠BCD，
∴∠EBD＝∠EDB，∠FDC＝∠BCD，
∴BE＝DE，CF＝DF，AE＝AF，
∴等腰三角形有△ABC，△AEF，△DEB，△DFC，△BDC共5个，
∴BE+CF＝DE+DF＝EF，
即BE+CF＝EF，
△AEF的周长＝AE+EF+AF＝AE+BE+AF+FC＝AB+AC＝20．
故答案为：5；BE+CF＝EF；20；
（2）BE+CF＝EF，
∵BD平分∠ABC，CD平分∠ACB，
∴∠EBD＝∠CBD，∠FCD＝∠BCD，
∵EF∥BC，
∴∠EDB＝∠CBD，∠FDC＝∠BCD，
∴∠EBD＝∠EDB，∠FDC＝∠BCD，
∴BE＝DE，CF＝DF，
∴等腰三角形有△BDE，△CFD，
∴BE+CF＝DE+DF＝EF，即BE+CF＝EF．
可得△AEF的周长为18．
（3）BE﹣CF＝EF，
由（1）知BE＝ED，
∵EF∥BC，
∴∠EDC＝∠DCG＝∠ACD，
∴CF＝DF，
又∵ED﹣DF＝EF，
∴BE﹣CF＝EF．
题型二等边三角形
9．关于等边三角形，下列说法中错误的是（ ）
A．等边三角形中，各边都相等
B．等腰三角形是特殊的等边三角形
C．两个角都等于60°的三角形是等边三角形
D．有一个角为60°的等腰三角形是等边三角形
【答案】B
【解析】
解：A、等边三角形中，各边都相等，此选项正确；
B、等边三角形是特殊的等腰三角形，此选项错误；
C、两个角都等于60°的三角形是等边三角形，此选项正确；
D、有一个角为60°的等腰三角形是等边三角形，此选项正确；
故选：B．
10．如图，△ABC是等边三角形，P是三角形内任意一点，D、E、F分别是AC、AB、BC边上的三点，且PF∥AB，PD∥BC，PE∥AC．若PF+PD+PE＝a，则△ABC的边长为（ ）
A．aB．aC．aD．a
【答案】D
【解析】解：延长EP交BC于点G，延长FP交AC于点H，如图所示：
∵PF∥AB，PD∥BC，PE∥AC，
∴四边形AEPH、四边形PDCG均为平行四边形，
∴PE＝AH，PG＝CD．
又∵△ABC为等边三角形，
∴△FGP和△HPD也是等边三角形，
∴PF＝PG＝CD，PD＝DH，
∴PE+PD+PF＝AH+DH+CD＝AC，
∴AC＝a；
故选：D．
11．如图，△MNP中，∠P＝60°，MN＝NP，MQ⊥PN，垂足为Q，延长MN至G，取NG＝NQ，若△MNP的周长为12，MQ＝a，则△MGQ周长是（ ）
A．8+2aB．8+aC．6+aD．6+2a
【答案】D
【解析】解：∵△MNP中，∠P＝60°，MN＝NP
∴△MNP是等边三角形．
又∵MQ⊥PN，垂足为Q，
∴PM＝PN＝MN＝4，NQ＝NG＝2，MQ＝a，∠QMN＝30°，∠PNM＝60°，
∵NG＝NQ，
∴∠G＝∠QMN，
∴QG＝MQ＝a，
∵△MNP的周长为12，
∴MN＝4，NG＝2，
∴△MGQ周长是6+2a．
故选：D．
12．如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．∠ADC＝30°，AD＝3，BD＝5，则CD的长为（ ）
A．B．4C．D．4.5
【答案】B
【解析】解：如图，以CD为边作等边△CDE，连接AE．
∵∠BCD＝∠BCA+∠ACD＝∠DCE+∠ACD＝∠ACE，
∴在△BCD和△ACE中，
，
∴△BCD≌△ACE（SAS），
∴BD＝AE．
又∵∠ADC＝30°，
∴∠ADE＝90°．
在Rt△ADE中，AE＝5，AD＝3，
于是DE＝，
∴CD＝DE＝4．
故选：B．
13．如图，AB＝AC，AE＝EC＝CD，∠A＝60°，若EF＝2，则DF＝（ ）
A．3B．4C．5D．6
【答案】D
【解析】解：如图，过点E作EG⊥BC，交BC于点G
∵AB＝AC，∠A＝60°，
∴△ABC是等边三角形，
∴∠ACB＝60°，
∵EC＝CD，
∴∠CED＝∠CDE＝∠ACB＝30°，
∴∠AEF＝30°，
∴∠AFE＝90°，即EF⊥AB，
∵△ABC是等边三角形，AE＝CE，
∴BE平分∠ABC，
∴EG＝EF＝2，
在Rt△DEG中，DE＝2EG＝4，
∴DF＝EF+DE＝2+4＝6；
方法二、
∵AB＝AC，∠A＝60°，
∴△ABC是等边三角形，
∴∠ACB＝60°，
∵EC＝CD，
∴∠CED＝∠CDE＝∠ACB＝30°，
∵△ABC是等边三角形，AE＝CE，
∴BE平分∠ABC，
∴∠ABE＝∠CBE＝30°＝∠CDE，
∴BE＝DE，∠BFD＝90°，
∴BE＝2EF＝4＝DE，
∴DF＝DE+EF＝6；
故选：D．
14．如图，△ABC是等边三角形，DF⊥AB，DE⊥CB，EF⊥AC，求证：△DEF是等边三角形．
【解析】
证明：∵△ABC是等边三角形，
∴AB＝AC＝BC，∠ABC＝∠ACB＝∠CAB＝60°，
∵DF⊥AB，DE⊥CB，EF⊥AC，
∴∠DAB＝∠ACF＝∠CBE＝90°，
∴∠FAC＝∠BCE＝∠DBA＝30°，
∴∠D＝∠E＝∠F＝180°﹣90°﹣30°＝60°，
∴DF＝DE＝EF，
∴△DEF是等边三角形．
15．如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC，∠OCD＝60°，连接OD．
（1）求证：△OCD是等边三角形；
（2）当α＝150°时，试判断△AOD的形状，并说明理由；
（3）探究：当α为多少度时，△AOD是等腰三角形．
【解析】
解：（1）∵△BOC≌△ADC，
∴OC＝DC，
∵∠OCD＝60°，
∴△OCD是等边三角形．
（2）△AOD是直角三角形．
理由如下：
∵△OCD是等边三角形，
∴∠ODC＝60°，
∵△BOC≌△ADC，α＝150°，
∴∠ADC＝∠BOC＝α＝150°，
∴∠ADO＝∠ADC﹣∠ODC＝150°﹣60°＝90°，
∴△AOD是直角三角形．
（3）∵△OCD是等边三角形，
∴∠COD＝∠ODC＝60°．
∵∠AOB＝110°，∠ADC＝∠BOC＝α，
∴∠AOD＝360°﹣∠AOB﹣∠BOC﹣∠COD＝360°﹣110°﹣α﹣60°＝190°﹣α，
∠ADO＝∠ADC﹣∠ODC＝α﹣60°，
∴∠OAD＝180°﹣∠AOD﹣∠ADO＝180°﹣（190°﹣α）﹣（α﹣60°）＝50°．
①当∠AOD＝∠ADO时，190°﹣α＝α﹣60°，
∴α＝125°．
②当∠AOD＝∠OAD时，190°﹣α＝50°，
∴α＝140°．
③当∠ADO＝∠OAD时，
α﹣60°＝50°，
∴α＝110°．
综上所述：当α＝110°或125°或140°时，△AOD是等腰三角形．
题型三直角三角形
16．下列条件中，不能确定一个直角三角形的条件是（ ）
A．已知两条直角边B．已知两个锐角
C．已知一边和一个锐角D．已知一条直角边和斜边
【答案】B
【解析】
解：A、已知两条直角边，可以确定一个直角三角形；
B、一直两个锐角，若两个锐角的和不等于90°，则不能确定一个直角三角形；
C、已知一边和一个锐角，可以得到一直角，则能确定一个直角三角形；
D、已知一条直角边和斜边，可以确定一个直角三角形．
故选：B．
17．如图，在直角三角形ABC中，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（除∠C外）相等的角的个数是（ ）
A．2B．3C．4D．5
【答案】B
【解析】解：
∵AD是斜边BC上的高，DE⊥AC，DF⊥AB，
∴∠C+∠B＝90°，∠BDF+∠B＝90°，∠BAD+∠B＝90°，
∴∠C＝∠BDF＝∠BAD，
∵∠DAC+∠C＝90°，∠DAC+∠ADE＝90°，
∴∠C＝∠ADE，
∴图中与∠C（除之∠C外）相等的角的个数是3，
故选：B．
18．如图，已知直角△ABC中，∠BAC＝90°，∠B＝56°，AD⊥BC，DE∥CA．∠ADE的度数为（ ）
A．56°B．34°C．44°D．46°
【答案】A
【解析】解：∵∠BAC＝90°，DE∥AC（已知）
∴∠DEA＝180°﹣∠BAC＝90°（两直线平行，同旁内角互补）．
∵AD⊥BC，∠B＝56°，
∴∠BAD＝34°，
在△ADE中，∵DE⊥AB，
∴∠ADE＝56°．
故选：A．
19．如图，△ABC中，∠BAC＝90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC，给出下列结论：①∠BAD＝∠C；②∠AEF＝∠AFE；③∠EBC＝∠C；④AG⊥EF．其中正确的结论是（ ）
A．②③④B．①③④C．①②④D．①②③
【答案】C
【解析】解：∵∠BAC＝90°，AD⊥BC，
∴∠C+∠ABC＝90°，
∠BAD+∠ABC＝90°，
∴∠BAD＝∠C，故①正确；
∵BE是∠ABC的平分线，
∴∠ABE＝∠CBE，
∵∠ABE+∠AEF＝90°，
∠CBE+∠BFD＝90°，
∴∠AEF＝∠BFD，
又∵∠AFE＝∠BFD（对顶角相等），
∴∠AEF＝∠AFE，故②正确；
∵∠ABE＝∠CBE，
∴只有∠C＝30°时∠EBC＝∠C，故③错误；
∵∠AEF＝∠AFE，
∴AE＝AF，
∵AG平分∠DAC，
∴AG⊥EF，故④正确．
综上所述，正确的结论是①②④．
故选：C．
20．如图，在Rt△ABC中，∠C＝90°，点E在AC边上且2∠CBE＝∠ABE，过点A作AD∥BC，AD与BE的延长线交于点D，DE＝，则AB＝ ．
【答案】
【解析】解：如图，取DE的中点F，连接AF，
∵AD∥BC，∠C＝90°．
∴∠D＝∠CBE，∠EAD＝90°，
∵2∠CBE＝∠ABE
∴∠ABE＝2∠D，
∵F为DE的中点，
∴AF＝DF＝EF，
∴∠D＝∠FAD，
∵∠AFB＝∠D+∠FAD，
∴∠AFB＝∠ABF，
∴AB＝AF＝DE，
∵DE＝，
∴AB＝．
故答案为：．
21．直线EF、GH之间有一个直角三角形ABC，其中∠BAC＝90°，∠ABC＝α．
（1）如图1，点A在直线EF上，B、C在直线GH上，若∠α＝60°，∠FAC＝30°．试说明：EF∥GH；
（2）将三角形ABC如图2放置，直线EF∥GH，点C、B分别在直线EF、GH上，且BC平分∠ABH．求∠ECA的度数；（用α的代数式表示）
（3）在（2）的前提下，直线CD平分∠FCA交直线GH于D，如图3．在α取不同数值时，∠BCD的大小是否发生变化？若不变求其值，若变化请求出变化的范围．
【解析】（1）证明：∵∠EAB＝180°﹣∠BAC﹣∠FAC，∠BAC＝90°，∠FAC＝30°，
∴∠EAB＝60°，
又∵∠ABC＝60°，
∴∠EAB＝∠ABC，
∴EF∥GH；
（2）解：∵∠BAC＝90°，∠ABC＝α．
∴∠ACB＝90°﹣α，
∵BC平分∠ABH，
∴∠ABC＝∠HBC＝α，
∵EF∥GH，
∴∠ECB＝∠HBC＝α，
∴∠ECA＝∠ECB﹣∠ACB＝α﹣（90°﹣α）＝2α﹣90°；
（3）解：不发生变化，
理由是：经过点A作AM∥GH，
又∵EF∥GH，
∴AM∥EF∥GH，
∴∠FCA+∠CAM＝180°，∠MAB+∠ABH＝180°，∠CBH＝∠ECB，
又∵∠CAM+∠MAB＝∠BAC＝90°，
∴∠FCA+∠ABH＝270°，
又∵BC平分∠ABH，CD平分∠FCA，
∴∠FCD+∠CBH＝135°，
又∵∠CBH＝∠ECB，即∠FCD+∠ECB＝135°，
∴∠BCD＝180°﹣（∠FCD+∠ECB）＝45°．
22．小明在学习三角形知识时，发现如下三个有趣的结论：在Rt△ABC中，∠A＝90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．
（1）M为边AC上一点，则BD、MF的位置是 ．请你进行证明．
（2）M为边AC反向延长线上一点，则BD、MF的位置关系是 ．请你进行证明．
（3）M为边AC延长线上一点，猜想BD、MF的位置关系是 ．请你进行证明．
【解析】解：（1）BD∥MF．
理由如下：∵∠A＝90°，ME⊥BC，
∴∠ABC+∠AME＝360°﹣90°×2＝180°，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD＝∠ABC，∠AMF＝∠AME，
∴∠ABD+∠AMF＝（∠ABC+∠AME）＝90°，
又∵∠AFM+∠AMF＝90°，
∴∠ABD＝∠AFM，
∴BD∥MF；
（2）BD⊥MF．
理由如下：∵∠A＝90°，ME⊥BC，
∴∠ABC+∠C＝∠AME+∠C＝90°，
∴∠ABC＝∠AME，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD＝∠AMF，
∵∠ABD+∠ADB＝90°，
∴∠AMF+∠ADB＝90°，
∴BD⊥MF；
（3）BD⊥MF．
理由如下：∵∠A＝90°，ME⊥BC，
∴∠ABC+∠ACB＝∠AME+∠ACB＝90°，
∴∠ABC＝∠AME，
∵BD平分∠ABC，MF平分∠AME，
∴∠ABD＝∠AMF，
∵∠AMF+∠F＝90°，
∴∠ABD+∠F＝90°，
∴BD⊥MF．