




所属成套资源:备战2024年中考数学一轮复习重难题型(全国通用)
- 专题22 二次函数与几何图形综合题(与三角形全等或三角形相似有关问题)-备战2024年中考数学一轮复习重难题型(全国通用) 试卷 0 次下载
- 专题23 二次函数与几何图形综合题(与特殊四边形有关问题)-备战2024年中考数学一轮复习重难题型(全国通用) 试卷 0 次下载
- 专题25 几何探究以四边形的性质为背景(动点、平移、旋转、折叠)-备战2024年中考数学一轮复习重难题型(全国通用) 试卷 0 次下载
- 专题26 几何探究以三角形为背景(动点、平移、旋转、折叠)-备战2024年中考数学一轮复习重难题型(全国通用) 试卷 0 次下载
- 专题27 几何探究以二次函数性质为背景(动点、平移、旋转、折叠)-备战2024年中考数学一轮复习重难题型(全国通用) 试卷 0 次下载
专题24 二次函数与几何图形综合题(与圆有关问题)-备战2024年中考数学一轮复习重难题型(全国通用)
展开
这是一份专题24 二次函数与几何图形综合题(与圆有关问题)-备战2024年中考数学一轮复习重难题型(全国通用),文件包含专题24二次函数与几何图形综合题与圆有关问题原卷版docx、专题24二次函数与几何图形综合题与圆有关问题解析版docx等2份试卷配套教学资源,其中试卷共80页, 欢迎下载使用。
2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系,寻求代数问题的解决方法(以形助数),或利用数量关系来研究几何图形的性质,解决几何问题(以数助形)的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来,不等于“一点不懂、一点不会”,要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时,我们通常是将未知问题转化为已知的问题,将复杂的问题转化为简单的问题,将抽象的问题转化为具体的问题,将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论,就有可能造成错解或漏解,纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题,把不熟悉的问题转化为熟悉的问题,把未知的问题转化为已知的问题。
专题24二次函数与几何图形综合题(与圆有关问题)
1.(2023·山东烟台·统考中考真题)如图,抛物线与轴交于两点,与轴交于点.抛物线的对称轴与经过点的直线交于点,与轴交于点.
(1)求直线及抛物线的表达式;
(2)在抛物线上是否存在点,使得是以为直角边的直角三角形?若存在,求出所有点的坐标;若不存在,请说明理由;
(3)以点为圆心,画半径为2的圆,点为上一个动点,请求出的最小值.
2.(2023·江苏苏州·统考中考真题)如图,二次函数的图像与轴分别交于点(点A在点的左侧),直线是对称轴.点在函数图像上,其横坐标大于4,连接,过点作,垂足为,以点为圆心,作半径为的圆,与相切,切点为.
(1)求点的坐标;
(2)若以的切线长为边长的正方形的面积与的面积相等,且不经过点,求长的取值范围.
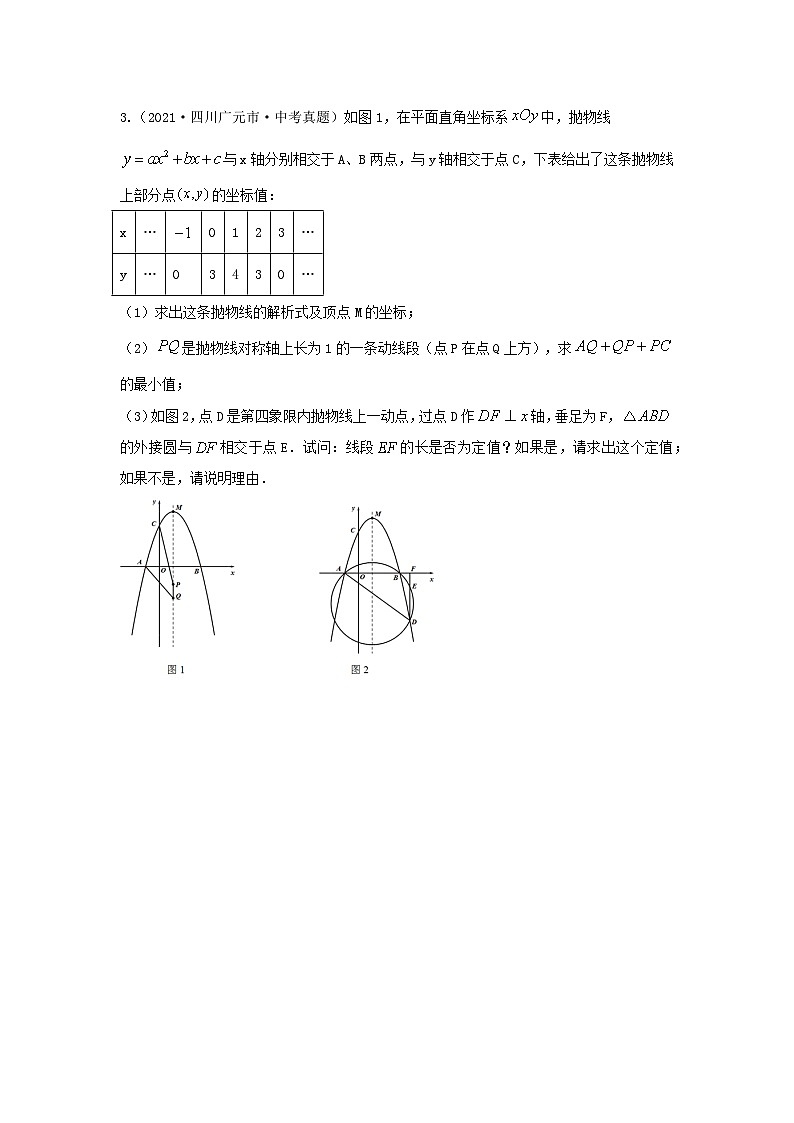
3.(2021·四川广元市·中考真题)如图1,在平面直角坐标系中,抛物线与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点的坐标值:
(1)求出这条抛物线的解析式及顶点M的坐标;
(2)是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求的最小值;
(3)如图2,点D是第四象限内抛物线上一动点,过点D作轴,垂足为F,的外接圆与相交于点E.试问:线段的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
4.(2023·四川自贡·统考中考真题)如图,抛物线与x轴交于,两点,与轴交于点.
(1)求抛物线解析式及,两点坐标;
(2)以,,,为顶点的四边形是平行四边形,求点坐标;
(3)该抛物线对称轴上是否存在点,使得,若存在,求出点的坐标;若不存在,请说明理由.
5.(2021·四川中考真题)如图,在平面直角坐标系中,抛物线交轴于点和,交轴于点,抛物线的对称轴交轴于点,交抛物线于点.
(1)求抛物线的解析式;
(2)将线段绕着点沿顺时针方向旋转得到线段,旋转角为,连接,,求的最小值.
(3)为平面直角坐标系中一点,在抛物线上是否存在一点,使得以,,,为顶点的四边形为矩形?若存在,请直接写出点的横坐标;若不存在,请说明理由;
6.(2023·重庆·统考中考真题)如图,在平面直角坐标系中,抛物线与轴交于点,,与轴交于点,其中,.
(1)求该抛物线的表达式;
(2)点是直线下方抛物线上一动点,过点作于点,求的最大值及此时点的坐标;
(3)在(2)的条件下,将该抛物线向右平移个单位,点为点的对应点,平移后的抛物线与轴交于点,为平移后的抛物线的对称轴上任意一点.写出所有使得以为腰的是等腰三角形的点的坐标,并把求其中一个点的坐标的过程写出来.
7.(2021·四川中考真题)如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.
(1)求抛物线的表达式;
(2)判断△BCE的形状,并说明理由;
(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP的值最小,若存在,请求出最小值;若不存在,请说明理由.
8.(2023·湖南·统考中考真题)如图,二次函数的图象与轴交于,两点,与轴交于点,其中,.
(1)求这个二次函数的表达式;
(2)在二次函数图象上是否存在点,使得?若存在,请求出点坐标;若不存在,请说明理由;
(3)点是对称轴上一点,且点的纵坐标为,当是锐角三角形时,求的取值范围.
9.(2021·湖南中考真题)如图,已知二次函数的图象经过点且与轴交于原点及点.
(1)求二次函数的表达式;
(2)求顶点的坐标及直线的表达式;
(3)判断的形状,试说明理由;
(4)若点为上的动点,且的半径为,一动点从点出发,以每秒2个单位长度的速度沿线段匀速运动到点,再以每秒1个单位长度的速度沿线段匀速运动到点后停止运动,求点的运动时间的最小值.
10.(2023·四川乐山·统考中考真题)已知是抛物(b为常数)上的两点,当时,总有
(1)求b的值;
(2)将抛物线平移后得到抛物线.
探究下列问题:
①若抛物线与抛物线有一个交点,求m的取值范围;
②设抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的顶点为点E,外接圆的圆心为点F,如果对抛物线上的任意一点P,在抛物线上总存在一点Q,使得点P、Q的纵坐标相等.求长的取值范围.
11.(2020•德州)如图1,在平面直角坐标系中,点A的坐标是(0,﹣2),在x轴上任取一点M,连接AM,分别以点A和点M为圆心,大于12AM的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为 ,其理由为: .
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L,猜想曲线L的形状是 .
验证:
(4)设点P的坐标是(x,y),根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
(5)如图3,点B(﹣1,3),C(1,3),点D为曲线L上任意一点,且∠BDC<30°,求点D的纵坐标yD的取值范围.
12.(2023·湖南·统考中考真题)已知二次函数.
(1)若,且该二次函数的图像过点,求的值;
(2)如图所示,在平面直角坐标系中,该二次函数的图像与轴交于点,且,点D在上且在第二象限内,点在轴正半轴上,连接,且线段交轴正半轴于点,.
①求证:.
②当点在线段上,且.的半径长为线段的长度的倍,若,求的值.
13.(2020•济宁)我们把方程(x﹣m)2+(y﹣n)2=r2称为圆心为(m,n)、半径长为r的圆的标准方程.例如,圆心为(1,﹣2)、半径长为3的圆的标准方程是(x﹣1)2+(y+2)2=9.在平面直角坐标系中,⊙C与轴交于点A,B,且点B的坐标为(8,0),与y轴相切于点D(0,4),过点A,B,D的抛物线的顶点为E.
(1)求⊙C的标准方程;
(2)试判断直线AE与⊙C的位置关系,并说明理由.
14.(2023·湖南·统考中考真题)如图,在平面直角坐标系中,抛物线经过点和点,且与直线交于两点(点在点的右侧),点为直线上的一动点,设点的横坐标为.
(1)求抛物线的解析式.
(2)过点作轴的垂线,与拋物线交于点.若,求面积的最大值.
(3)抛物线与轴交于点,点为平面直角坐标系上一点,若以为顶点的四边形是菱形,请求出所有满足条件的点的坐标.
15.(2020•遵义)如图,抛物线y=ax2+94x+c经过点A(﹣1,0)和点C(0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
(1)求该抛物线的解析式;
(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.
16.(2023·四川宜宾·统考中考真题)如图,抛物线与x轴交于点、,且经过点.
(1)求抛物线的表达式;
(2)在x轴上方的抛物线上任取一点N,射线、分别与抛物线的对称轴交于点P、Q,点Q关于x轴的对称点为,求的面积;
(3)点M是y轴上一动点,当最大时,求M的坐标.
17.(2023·湖南怀化·统考中考真题)如图一所示,在平面直角坐标系中,抛物线与轴交于两点,与轴交于点.
(1)求抛物线的函数表达式及顶点坐标;
(2)点为第三象限内抛物线上一点,作直线,连接、,求面积的最大值及此时点的坐标;
(3)设直线交抛物线于点、,求证:无论为何值,平行于轴的直线上总存在一点,使得为直角.
18.(2020·江苏苏州?中考真题)如图,已知,是的平分线,是射线上一点,.动点从点出发,以的速度沿水平向左作匀速运动,与此同时,动点从点出发,也以的速度沿竖直向上作匀速运动.连接,交于点.经过、、三点作圆,交于点,连接、.设运动时间为,其中.
(1)求的值;
(2)是否存在实数,使得线段的长度最大?若存在,求出的值;若不存在,说明理由.
(3)求四边形的面积.
19.(2020·山东济宁?中考真题)我们把方程(x- m)2+(y-n)2=r2称为圆心为(m,n)、半径长为r的圆的标准方程.例如,圆心为(1,-2)、半径长为3的圆的标准方程是(x- 1)2+(y+2)2=9.在平面直角坐标系中,圆C与轴交于点A.B.且点B的坐标为(8.0),与y轴相切于点D(0, 4),过点A,B,D的抛物线的顶点为E.
(1)求圆C的标准方程;
(2)试判断直线AE与圆C的位置关系,并说明理由.
x
…
0
1
2
3
…
y
…
0
3
4
3
0
…
M的坐标
…
(﹣2,0)
(0,0)
(2,0)
(4,0)
…
P的坐标
…
(0,﹣1)
(2,﹣2)
…
相关试卷
这是一份专题20 二次函数与几何图形综合题(与面积问题)-备战2024年中考数学一轮复习重难题型(全国通用),文件包含专题20二次函数与几何图形综合题与面积问题原卷版docx、专题20二次函数与几何图形综合题与面积问题解析版docx等2份试卷配套教学资源,其中试卷共95页, 欢迎下载使用。
这是一份专题19 二次函数与几何图形综合题(与线段问题)-备战2024年中考数学一轮复习重难题型(全国通用),文件包含专题19二次函数与几何图形综合题与线段问题原卷版docx、专题19二次函数与几何图形综合题与线段问题解析版docx等2份试卷配套教学资源,其中试卷共71页, 欢迎下载使用。
这是一份专题18 二次函数与几何图形综合题(与角度问题)-备战2024年中考数学一轮复习重难题型(全国通用),文件包含专题18二次函数与几何图形综合题与角度问题原卷版docx、专题18二次函数与几何图形综合题与角度问题解析版docx等2份试卷配套教学资源,其中试卷共72页, 欢迎下载使用。








