江苏省苏州市苏州高新区实验初级中学2023-2024学年八年级下学期3月月考数学试题

这是一份江苏省苏州市苏州高新区实验初级中学2023-2024学年八年级下学期3月月考数学试题，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

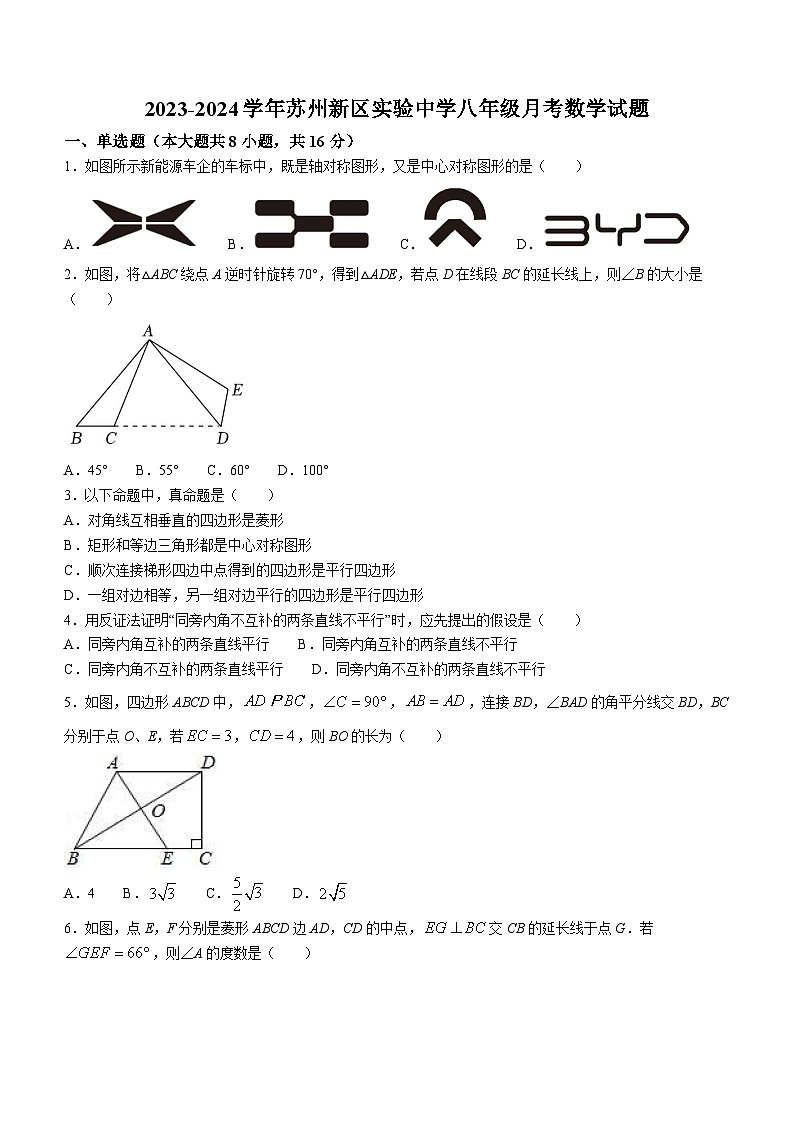
1．如图所示新能源车企的车标中，既是轴对称图形，又是中心对称图形的是（ ）
A． B． C． D．
2．如图，将△ABC绕点A逆时针旋转70°，得到△ADE，若点D在线段BC的延长线上，则∠B的大小是（ ）
A．45° B．55° C．60° D．100°
3．以下命题中，真命题是（ ）
A．对角线互相垂直的四边形是菱形
B．矩形和等边三角形都是中心对称图形
C．顺次连接梯形四边中点得到的四边形是平行四边形
D．一组对边相等，另一组对边平行的四边形是平行四边形
4．用反证法证明“同旁内角不互补的两条直线不平行”时，应先提出的假设是（ ）
A．同旁内角互补的两条直线平行 B．同旁内角互补的两条直线不平行
C．同旁内角不互补的两条直线平行 D．同旁内角不互补的两条直线不平行
5．如图，四边形ABCD中，，，，连接BD，∠BAD的角平分线交BD，BC分别于点O、E，若，，则BO的长为（ ）
A．4 B． C． D．
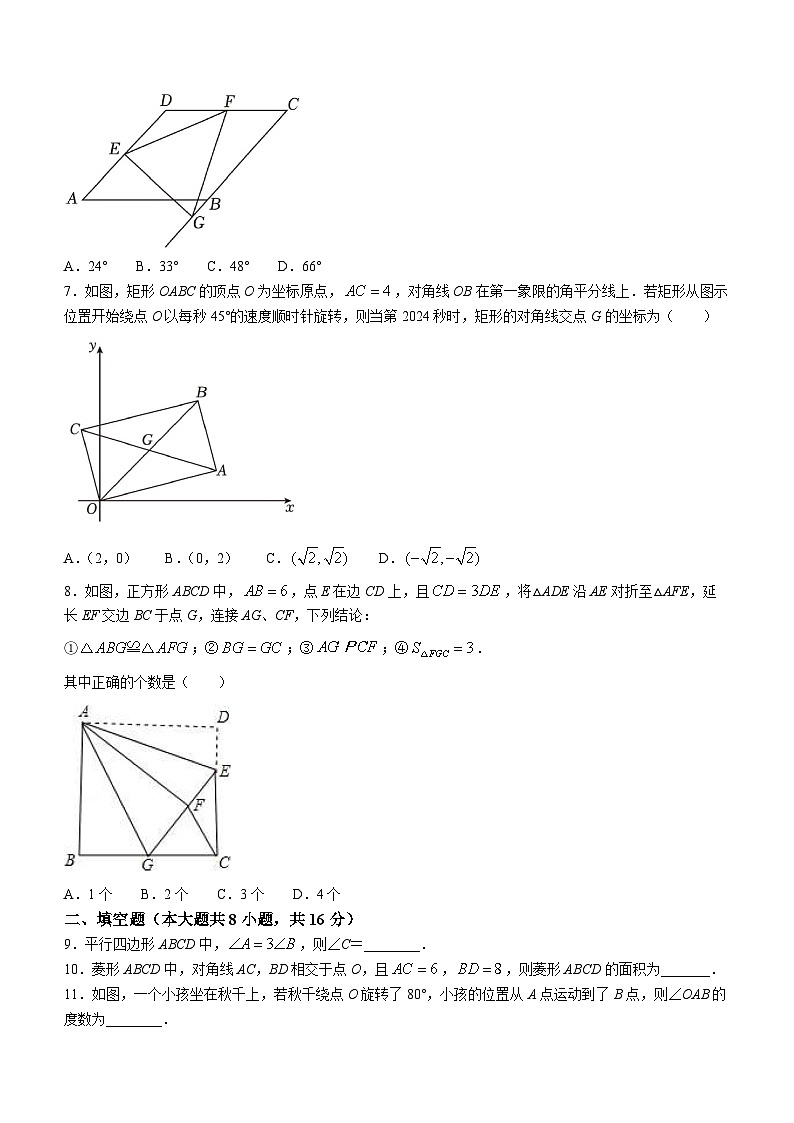
6．如图，点E，F分别是菱形ABCD边AD，CD的中点，交CB的延长线于点G．若，则∠A的度数是（ ）
A．24° B．33° C．48° D．66°
7．如图，矩形OABC的顶点O为坐标原点，，对角线OB在第一象限的角平分线上．若矩形从图示位置开始绕点O以每秒45°的速度顺时针旋转，则当第2024秒时，矩形的对角线交点G的坐标为（ ）
A．（2，0） B．（0，2） C． D．
8．如图，正方形ABCD中，，点E在边CD上，且，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：
①；②；③；④．
其中正确的个数是（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题（本大题共8小题，共16分）
9．平行四边形ABCD中，，则∠C＝________．
10．菱形ABCD中，对角线AC，BD相交于点O，且，，则菱形ABCD的面积为_______．
11．如图，一个小孩坐在秋千上，若秋千绕点O旋转了80°，小孩的位置从A点运动到了B点，则∠OAB的度数为________．
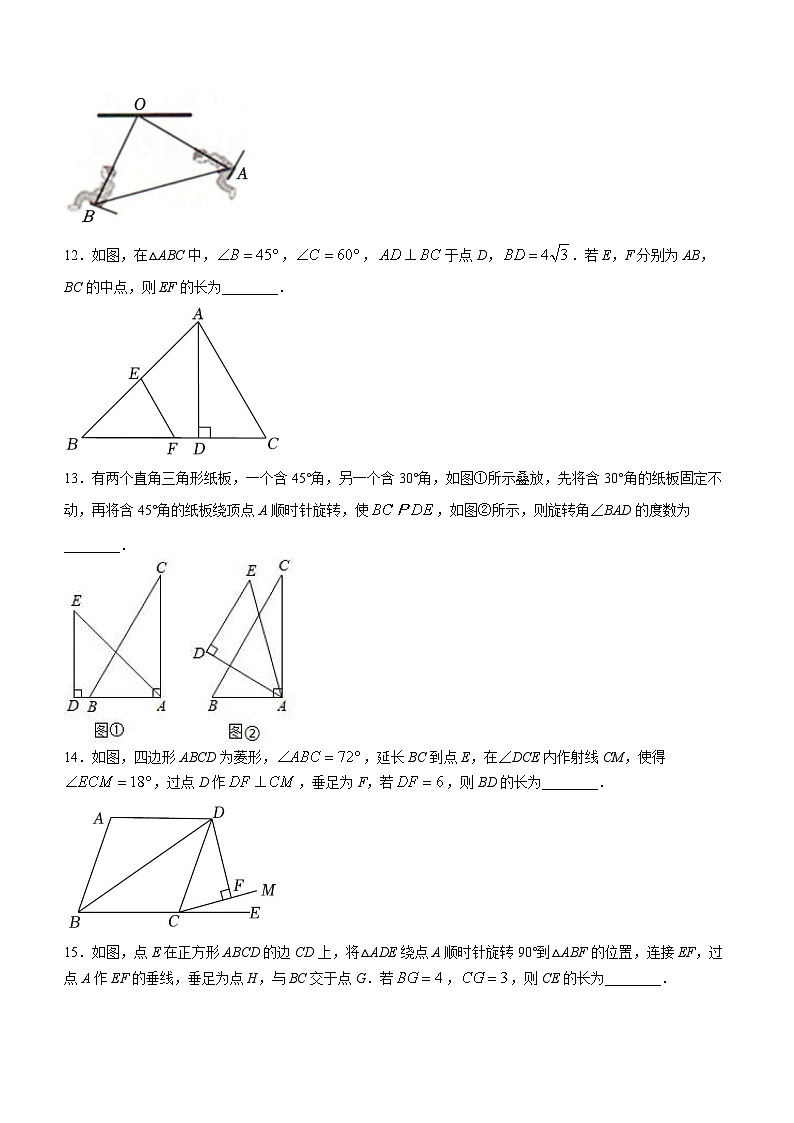
12．如图，在△ABC中，，，于点D，．若E，F分别为AB，BC的中点，则EF的长为________．
13．有两个直角三角形纸板，一个含45°角，另一个含30°角，如图①所示叠放，先将含30°角的纸板固定不动，再将含45°角的纸板绕顶点A顺时针旋转，使，如图②所示，则旋转角∠BAD的度数为________．
14．如图，四边形ABCD为菱形，，延长BC到点E，在∠DCE内作射线CM，使得，过点D作，垂足为F，若，则BD的长为________．
15．如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若，，则CE的长为________．
16．如图，在平面直角坐标系中，A（-1，0），B（0，2），点P是x轴上一动点，四边形ABPQ是平行四边形，当值最小时，点Q的坐标为________．
三、解答题（本大题共11小题，共68分）
17．（4分）如图，在Rt△ABC中，，，，将△ABC绕点C逆时针旋转得到△DEC，使点A的对应点D落在BC边上，点B的对应点为E，求线段BD，DE的长．
18．（4分）如图，在□ABCD中，BE、CF分别是∠ABC、∠BCD的平分线，若，．
（1）求□ABCD的周长；
（2）求线段EF的长．
19．（4分）如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上．
（1）将△ABC向右平移6个单位长度得到请画出；
（2）画出关于点O的中心对称图形；
（3）若将△ABC绕某一点旋转可得到，旋转中心的坐标为________．
20．（5分）如图，在△ABC中，，DE是△ABC的中位线，AF是△ABC的中线．求证：．
（1）请把证法1补充完整；（2）试用不同的方法证明．
21．（5分）如图1，某小区的大门是伸缩电动门，安装驱动器的门柱EFGH是宽度为30cm的矩形，伸缩电动门中有20个全等的菱形，每个菱形边长为30cm，大门的总宽度为10.3m．（门框的宽度忽略不计）
（1）当每个菱形的内角度数为60°（如图2）时，大门打开了多少m？
（2）当每个菱形的内角度数张开至为90°时，大门未完全关闭，有一辆宽1.8m的轿车需进入小区，计算说明该车能否直接通过．（参考数据：）
22．（5分）如图，已知点M在直线l外，点N在直线l上，完成下列问题：
（1）请用无刻度的直尺和圆规，以线段MN为一条对角线作菱形MPNQ，使菱形的边PN落在直线l上（要求保留作图痕迹，不写作法）；
（2）若点M到直线l的距离为4，MN的长为5，求这个菱形的边长．
23．（6分）如图，在平面直角坐标系xOy中，把矩形COAB绕点C顺时针旋转α角，得到矩形CFED．设FC与AB交于点H，且A（0，3），C（5，0）．
（1）当时，△CBD的形状是________；
（2）当旋转过程中，连接OH，当△OHC为等腰三角形时，求点H的坐标．
24．（6分）如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作于点E，延长BC到点F，使得，连接DF．
（1）求证：四边形AEFD是矩形；
（2）连接OE，若，，求AE的长．
25．（7分）如图，四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
（1）求证：；
（2）若，，求CG的长度；
（3）当线段DE与正方形ABCD的某条边的夹角是30°时，求∠EFC的度数．
26．（10分）在学习了“中心对称图形⋯平行四边形”这一章后，同学小明对特殊四边形的探究产生了浓厚的兴趣，他发现除了已经学过的特殊四边形外，还有很多比较特殊的四边形，勇于创新的他大胆地作出这样的定义：有一个内角是直角，且对角线互相垂直的四边形称为“双直四边形”．请你根据以上定义，回答下列问题：
（1）下列关于“双直四边形”的说法，正确的有_________（把所有正确的序号都填上）；
①“双直四边形”的对角线不可能相等：②“双直四边形”的面积等于对角线乘积的一半；
③若一个“双直四边形”是中心对称图形，则其一定是正方形．
（2）如图①，正方形ABCD中，点E、F分别在边AB、AD上，连接CE，BF，EF，CF，若，证明：四边形BCFE为“双直四边形”；
（3）如图②，在平面直角坐标系中，已知点A（0，6），C（8，0），点B在线段OC上且，是否存在点D在第一象限，使得四边形ABCD为“双直四边形”，若存在；求出所有点D的坐标，若不存在，请说明理由．
27．（12分）实践操作
在矩形ABCD中，，，现将纸片折叠，点D的对应点记为点P，折痕为EF（点E、F是折痕与矩形的边的交点），再将纸片还原．
初步思考
（1）若点P落在矩形ABCD的边AB上（如图①）．
当点P与点A重合时，_________°；当点E与点A重合时，________°；
深入探究
（2）当点E在AB上，点F在DC上时（如图②），求证：四边形DEPF为菱形，并直接写出当时的菱形EPFD的边长．
拓展延伸
（3）若点F与点C重合，点E在AD上，射线BA与射线FP交于点M（如图③）．在折叠过程中，是否存在使得线段AM与线段DE的长度相等的情况？若存在，请求出线段AE的长度；若不存在，请说明理由．
2023-2024学年苏州新区实验中学八年级月考数学试题
参考答案与解析
1．【分析】根据中心对称图形与轴对称图形的概念进行判断即可．
【解答】解：A、原图既是中心对称图形，又是轴对称图形，故此选项符合题意；
B、原图不是中心对称图形，是轴对称图形，故此选项不合题意；
C、原图不是中心对称图形，是轴对称图形，故此选项不合题意；
D、原图既不是中心对称图形，也不是轴对称图形，故此选项不合题意；
故选：A．
2．【分析】由旋转的性质可得，，由等腰三角形的性质可求解．
【解答】解：∵将△ABC绕点A逆时针旋转70°得到△ADE，
∴，，∴，
故选：B．
3．【分析】根据菱形的判定、中心对称图形的概念、平行四边形的判定判断即可．
【解答】解：A、对角线互相垂直的平行四边形是菱形，故本选项说法是假命题，不符合题意；
B、矩形是中心对称图形，而等边三角形不是中心对称图形，故本选项说法是假命题，不符合题意；
C、顺次连接梯形四边中点得到的四边形是平行四边形，是真命题，符合题意；
D、一组对边相等，另一组对边平行的四边形是平行四边形或梯形，故本选项说法是假命题，不符合题意；
故选：C．
4．【分析】首先明确什么反证法，然后根据命题“同旁内角不互补的两条直线不平行”可以得到应先假设什么，本题得以解决．
【解答】解：由题意可得，反证法证明命题“同旁内角不互补的两条直线不平行”时，应先假设同旁内角不互补的两条直线平行，故选：C．
5．【分析】连接DE，因为，，，可证四边形ABED为菱形，从而得到BE、BC的长，进而解答即可．
【解答】解：连接DE．
在直角三角形CDE中，，，根据勾股定理，得．
∵，AE平分∠BAD，∴，
∴AE垂直平分BD，．∴．
∵，∴，∴，
∴，∴，∴四边形ABED是菱形，
由勾股定理得出，∴，
故选：D．
6．【分析】连接AC，由菱形的性质推出，，判定，得到，求出，由三角形中位线定理推出，得到，即可求出．
【解答】解：连接AC，
∵四边形ABCD是菱形，∴，，
∵，∴，∴，
∵，∴，
∵E，F分别是AD，CD的中点，∴EF是△DAC的中位线，∴，
∴，∴，
故选：C．
7．【分析】求出OG，每秒旋转45°，8次一个循环，，第2024秒时，矩形的对角线交点G在第一象限，由此可得结论．
【解答】解：∵四边形ABCO是矩形，∴，，，
∴，∴，
∵每秒旋转45°，8次一个循环，，∴点G在第一象限，∴点G的坐标为．
故选：C．
8．【分析】根据翻折的性质可得，，，然后利用“HL”证明Rt△ABG和Rt△AFG全等，判断出①正确；根据全等三角形对应边相等可得，再根据“”求出DE的长，然后设，表示出CG、EG，然后利用勾股定理列出方程求出x，从而求出，判断出②正确；根据等边对等角可得，根据全等三角形对应角相等可得，再根据三角形的一个外角等于与它不相邻的两个内角的和可得，然后求出，再根据同位角相等，两直线平行可得，判断出③正确；然后求出△CEG的面积，再根据等高的三角形的面积的比等于底边的比求出△CGF的面积，判断出④错误．
【解答】解：∵△ADE沿AE对折至△AFE，∴，，，
∵四边形ABCD是正方形，∴，∴，
在Rt△ABG和Rt△AFG中，，∴，故①正确；
∴，
∵，，∴，，
设，则，，
在Rt△CEG中，，即，解得，
∴，故②正确；
∴，
由Rt△ABG和Rt△AFG得，，
由三角形的外角性质，，∴，∴，故③正确；
△CEG的面积，∴△CGF的面积，故④错误；
综上所述，正确的是①②③共3个．
故选：C．
9．【分析】由平行四边形的性质可得，，可得，即可求解．
【解答】解：∵四边形ABCD是平行四边形，∴，，∴，
∵，∴，∴，
故答案为：135°．
10．【分析】直接利用菱形的面积公式得出答案．
【解答】解：∵在菱形ABCD中，对角线AC、BD相交于点O，，，
∴菱形ABCD的面积是：．
故答案为：24．
11．【分析】先根据题意得到，，再根据等腰三角形的性质和三角形内角和定理进行解答即可．
【解答】解：由题意可知：，，
∵，∴，
∵，∴，
∴，
故答案为：50°．
12．【分析】根据等腰直角三角形的性质求出AD，根据正弦的定义求出AC，根据三角形这中位线定理计算即可．
【解答】解：在Rt△ADB中，，，
∴，则，
∵E，F分别为AB，BC的中点，∴EF是△ABC的中位线，∴，
故答案为：4．
13．【分析】由平行线的性质可得，由外角的性质可求∠BAD的度数．
【解答】解：如图，设AD与BC交于点F，
∵，∴，
∵，∴
故答案为：30°．
14．【分析】连接AC交BD于点H，先证，再证，得，即可得出答案．
【解答】解：如图，连接AC交BD于点H
∵四边形ABCD是菱形，，∴，，，，，
∴，，，
∵，∴，
∵，∴，∴，∴，
在△CDH和△CDF中，，∴，
∴，∴，
故答案为：12．
15．【分析】连接EG，根据AG垂直平分EF，即可得出，设，则，，再根据Rt△CEG中，，即可得到CE的长．
【解答】解：如图所示，连接EG，
由旋转可得，，∴，，
又∵，∴H为EF的中点，∴AG垂直平分EF，∴，
设，则，，∴，
∵，∴Rt△CEG中，，即，解得，
∴CE的长为，故答案为：．
16．【分析】先得出点Q是直线上的动点，再将转化成，考虑将军饮马．
【解答】解：A（-1，0），B（0，2），点P是x轴上一动点，四边形ABPQ是平行四边形，根据平移的性质得，∴点Q是直线上的动点，
作B（0，2）关于直线的对称点B′，连接B′Q、AB′，则B′（0，-6），
∵四边形ABPQ是平行四边形，∴，∴，
设直线AB′的表达式为，代入A（-1，0）得，，∴，
令，得，∴点Q的坐标为，
故答案为：．
17．【分析】由题意推出，所以，，，，再运用勾股定理，求得，即推出．
【解答】解：根据题意，得，∴，，
∵，∴，∵，∴，
在Rt△ABC中，根据勾股定理，得．∴．
18．【分析】（1）证出，则可得出答案；
（2）根据（1）可知，，同理可证：，则可求出答案．
【解答】解：（1）四边形ABCD是平行四边形，
∴，，∴，
∵BE平分∠ABC，∴，∴，∴，
∵，∴，
∴□ABCD的周长是：；
（2）根据（1）可知，，同理可证：，
则．
19．【分析】（1）利用平移变换的性质分别作出A，B，C的对应点，，即可；
（2）利用中心对称变换的性质分别作出，，的对应点，，即可；
（3）对应点连线的交点即为旋转中心．
【解答】解：（1）如图，即为所求；
（2）如图，即为所求；
（3）旋转中心Q的坐标为（-3，0），
故答案为：（-3，0）．
20．【分析】（1）根据三角形中位线定理得到，根据直角三角形的性质得到，等量代换证明结论；
（2）连接DF、EF，根据三角形中位线定理得到，，证明四边形ADFE是矩形，根据矩形的对角线相等证明即可．
【解答】解：（1）∵DE是△ABC的中位线，∴，
∵AF是△ABC的中线，，∴，∴；
故答案为：；．
（2）连接DF、EF，
∵DE是△ABC的中位线，AF是△ABC的中线，∴DF、EF是△ABC的中位线，
∴，，∴四边形ADFE是平行四边形，
∵，∴四边形ADFE是矩形，∴．
21．【分析】（1）连接BD，根据菱形的性质可得，从而可得△ABD是等边三角形，然后利用等边三角形的性质可得，最后进行计算，即可解答；
（2）根据已知可得△ABD是等腰直角三角形，从而可得，然后进行计算即可解答．
【解答】解：（1）连接BD，
∵四边形ABCD是菱形，∴，
∵，∴△ABD是等边三角形，∴，
∴，
∵大门的总宽度为10.3m，∴大门打开的宽度，∴大门打开了4m；
（2）该车不能直接通过，
理由：∵，，∴，
∴
∵大门的总宽度为10.3m，∴大门打开的宽度，
∵，∴该车不能直接通过．
22．【分析】（1）连接MN，作MN的垂直平分线交直线l于P，交MN于O点，然后截取，则四边形MPNQ满足条件；
（2）设菱形的边长为x，根据菱形的性质得到，，，根据菱形的面积公式得到，则，接着在Rt△OPM中利用勾股定理得到，然后解方程即可．
【解答】解：（1）如图，菱形MPNQ为所作；
（2）如图，设菱形的边长为x，
∵四边形MPNQ为菱形，，，，
∵点M到直线l的距离为4，MN的长为5，∴，∴，∴，，
在Rt△OPM中，，解得，
即这个菱形的边长为．
23．【分析】（1）根据有一个角是60°的等腰三角形是等边三角形即可判断；
（2）分三种情形分别求解即可解决问题；
【解答】解：（1）∵图形旋转后，，∴△BCD是等边三角形；
故答案为：等边三角形．
（2）①当时，在Rt△AHO中，，∴H（4，3）．
②当时，，∴H（2.5，3）．
③当时，，，∴H（1，3）
综上所述，点的坐标是（1，3）（2.5，3）（4，3）．
24．【分析】（1）先证，再证四边形AEFD是平行四边形，然后证，即可得出结论；
（2）由菱形的性质和直角三角形斜边上的中线性质得，，再由勾股定理得，则，然后由菱形面积公式即可解决问题．
【解答】（1）证明：∵四边形ABCD是菱形，∴且，
∵，∴，即，∴，
∵，∴四边形AEFD是平行四边形，
又∵，∴，∴平行四边形AEFD是矩形；
（2）解：∵四边形ABCD是菱形，，∴，，，，
∵，∴，∴，，
∴，∴，
∵菱形ABCD的面积，即，解得：．
25．【分析】（1）作于P，于Q，证明，得到；
（2）通过计算发现E是AC中点，点F与C重合，△CDG是等腰直角三角形，由此即可解决问题．
（3）分两种情形考虑问题即可；
【解答】（1）证明：作于P，于Q，
∵，∴，
∵，，∴，
在Rt△EQF和Rt△EPD中，，∴，∴，
（2）解：如图2中，在Rt△ABC中．，
∵，∴，∴点F与C重合，此时△DCG是等腰直角三角形，易知．
（3）解：①当DE与AD的夹角为30°时，点F在BC边上，，则，
在四边形CDEF中，由四边形内角和定理得：，
②当DE与DC的夹角为30°时，点F在BC的延长线上，，如图3所示：
∵，，∴，
综上所述，．
26．【分析】（1）由“双直四边形”的定义依次判断可求解；
（2）由“SAS”可证，可得，由余角的性质可证，可得结论；
（3）先求出BH的解析式，分两种情况讨论，将点D横坐标代入，即可求解．
【解答】（1）解：∵有一个内角是直角，且对角线互相垂直的四边形称为“双直四边形”，
∴正方形是“双直四边形”，“双直四边形”的面积等于对角线乘积的一半，故②正确；
∴“双直四边形”的对角线可能相等，故①错误
∵中心对称的四边形是平行四边形，且有一个内角是直角，对角线互相垂直，
∴这样的“双直四边形”是正方形，故③正确；
故答案为：②③；
（2）证明：设BF与CE交于点O，
∵四边形ABCD是正方形，∴，，
∵，∴，∴，∴，
∵，∴，∴，∴，
又∵，∴四边形BCFE为“双直四边形”；
（3）解：如图，设BD与AC交于点H，
∵点A（0，6），C（8，0），∴，，
∵，，∴，∴，
∴，∴点，
∵四边形ABCD为“双直四边形”，∴，
∵，∴，即点H是AC的中点，
∵点A（0，6），C（8，0），∴点H（4，3），
设直线BH的解析式为，∴，∴，
∴直线BH的解析式为，
当时，点D的横坐标为8，∴，∴点，
当时，∵，，∴BD是AC的垂直平分线，∴，
又∵，∴，∴，∴点，
当时，过点D作于E，于F，
同理可求点D（7，7），
综上所述：点D的坐标或（7，7）．
27．【分析】初步思考（1）当点P与点A重合时，EF是AD的中垂线，，当点E与点A重合时，此时；
深入探究（2）当点E在AB上，点F在DC上时，EF是PD的中垂线，，，四边形ABCD是矩形，，，四边形DEPF是平行四边形，□DEPF为菱形，当时，设菱形的边长为x，则，，由勾股定理得：，进而求得AP；
拓展延伸（3）情况一：，，设，则，则，，求得AE；情况二，，，设，则，则，，，求得AE．
【解答】初步思考
（1）当点P与点A重合时，如图1，
∴EF是AD的中垂线，∴，
当点E与点A重合时，如图2，
此时，
故答案为：90，45；
深入探究
（2）当点E在AB上，点F在DC上时，如图3，
∵EF是PD的中垂线，∴，，
∵四边形ABCD是矩形，∴，∴，
∵，∴，∴，
∵，∴四边形DEPF是平行四边形，
∵，∴□DEPF为菱形，
当时，设菱形的边长为x，则，，
在Rt△ADE中，由勾股定理得：，
∴，∴，∴时的菱形EPFD的边长为：；
拓展延伸
（3）存在，
情况一：如图4，连接EM，
∵，∴，
设，则，则，
∵，，∴，∴，解得：；
情况二，如图5，
∵，∴，
设，则，则，，
则，，，∴，解得：，
综上，线段AE的长为：或．证法1：∵DE是△ABC的中位线，
∴________．
∵AF是△ABC的中线，，
∴________，
∴．