1.3探索三角形全等的条件(1)课件PPT

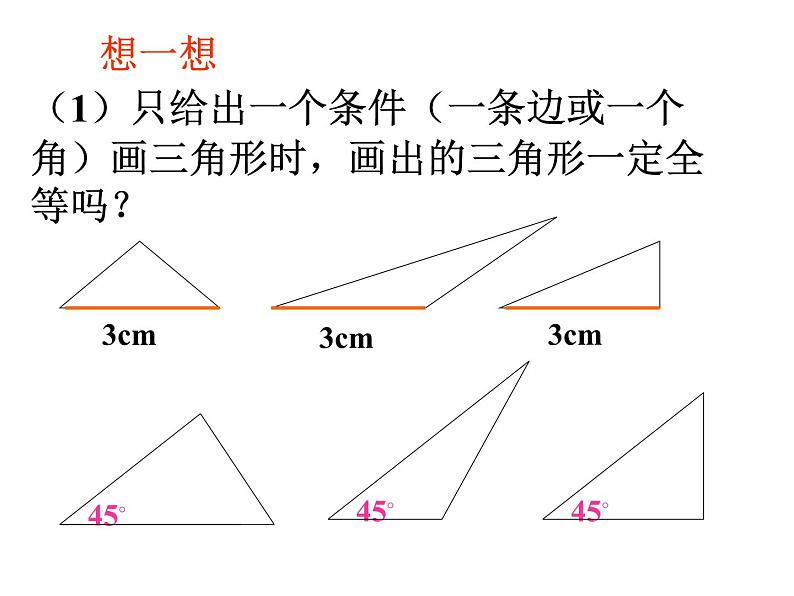
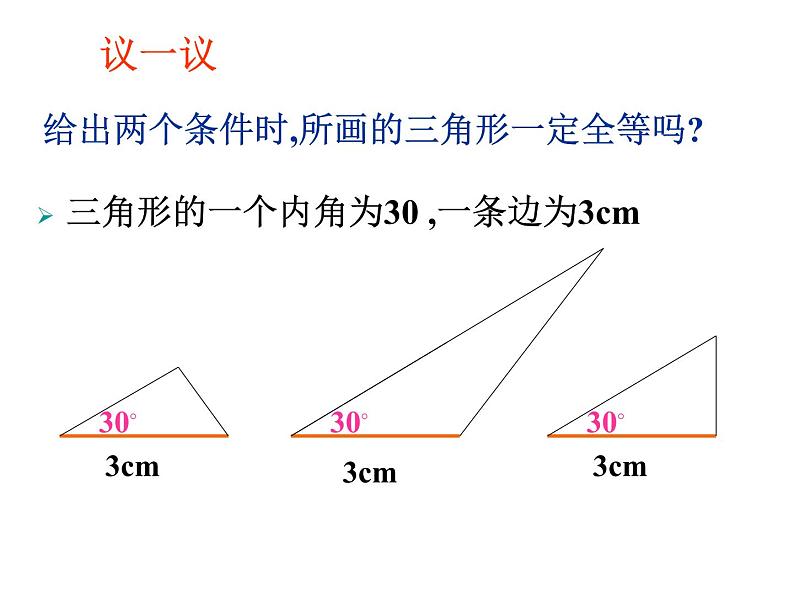
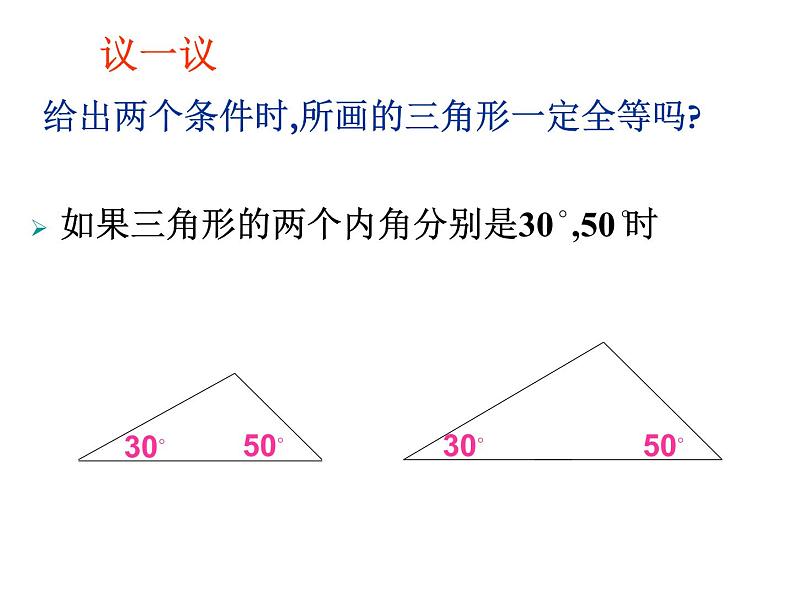
1.3 探索三角形全等的条件（1）问题引入小颖作业本上画的三角形被墨迹污染了，她想画一个与原来完全一样的三角形，她该怎么办？请你帮助小颖想一个办法，并说明你的理由？注意：与原来完全一样的三角形，即是与原来三角形全等的三角形. 要画一个三角形与小颖画的三角形全等.需要几个与边或角的大小有关的条件？只知道一个条件（一角或一边）行吗？两个条件呢？三个条件呢？让我们一起来探索三角形全等的条件想一想（1）只给出一个条件（一条边或一个角）画三角形时，画出的三角形一定全等吗？想一想1)三角形的一个内角为30°，一条边为3cm;2) 三角形的两个内角分别为30°和45°;3）三角形的两条边分别为4cm和6cm. 按下面的条件画三角形，画完后小组内交流，看所画的三角形是否全等.(其它条件不确定） （2）给出两个条件画三角形时，有几种可能的情况？每种情况下作出的三角形一定全等吗？想一想三角形的一个内角为30 ,一条边为3cm30◦给出两个条件时,所画的三角形一定全等吗?议一议给出两个条件时,所画的三角形一定全等吗?如果三角形的两个内角分别是30 ,50 时30◦30◦50◦50◦议一议给出两个条件时,所画的三角形一定全等吗?如果三角形的两边分别为4cm，6cm 时6cm6cm4cm4cm议一议30°只给两个条件作出三角形，不能保证所画出的三角形一定全等. 综上所述，只给出一个条件或两个条件时，都不能保证所画出的三角形一定全等. 想一想：如果给出三个条件画三角形时，你能说出有哪几种可能的情况吗？有四种可能：三条边、三个角、两边一角和两角一边.归纳总结1）与小组内的同学比较各自手中的三角尺，有没有三个内角对应相等的三角形，它们一定全等吗？和老师手中的三角板相比较呢？2）已知一个三角形的三条边分别为4cm、5cm、7cm，你能画出这个三角形吗？　　看老师的作图示范，再画出这个三角形，并与同伴画的三角形进行比较？它们一定全等吗？　　这说明有三个角对应相等的两个三角形不一定全等做一做 由此得出定理：三边对应相等的两个三角形全等，简写为“边边边”或“SSS” 这个定理说明，只要三角形的三边的长度确定了，这个三角形的形状和大小就完全确定了，这也是三角形具有稳定性的原理.　归纳总结 当我们同时给四边形和三角形外力时，会发现四边形要变形，而三角形不变形. 这就是三角形的特性－三角形的稳定性. 你能找出三角形的稳定性在生活中的应用吗？练习:如图，AB＝AC，BD＝CD，BH＝CH，图中有几组全等的三角形？它们全等的条件是什么？HDCBA解：有三组.在△ABH和△ACH中，因为AB=AC，BH=CH，AH=AH，所以△ABH≌△ACH（SSS）；在△ABH和△ACH中，因为AB=AC，BD=CD，AD=AD，所以△ABD≌△ACD（SSS）；在△ABH和△ACH中，因为BD=CD，BH=CH，DH=DH所以△DBH≌△DCH（SSS）．　课内练习 今天我们经历了画图验证两个三角形全等的过程，探索出两个三角形全等的条件之一“三边对应相等的两个三角形全等”，我们可以利用它来判别两个三角形是否全等.　　我们还知道了三角形具有稳定性，只要三角形的三边长度确定了，这个三角形的形状和大小就确定了.在生活中，三角形的稳定性有广泛的应用.小结