

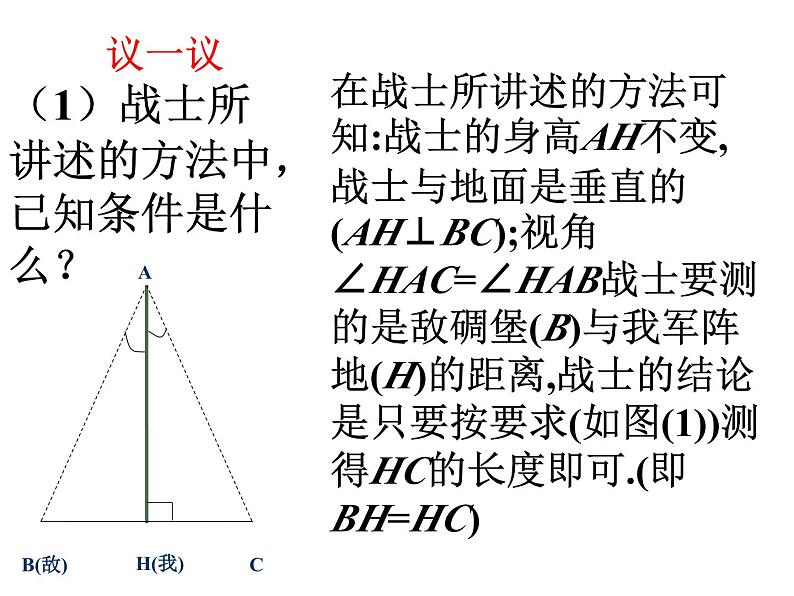
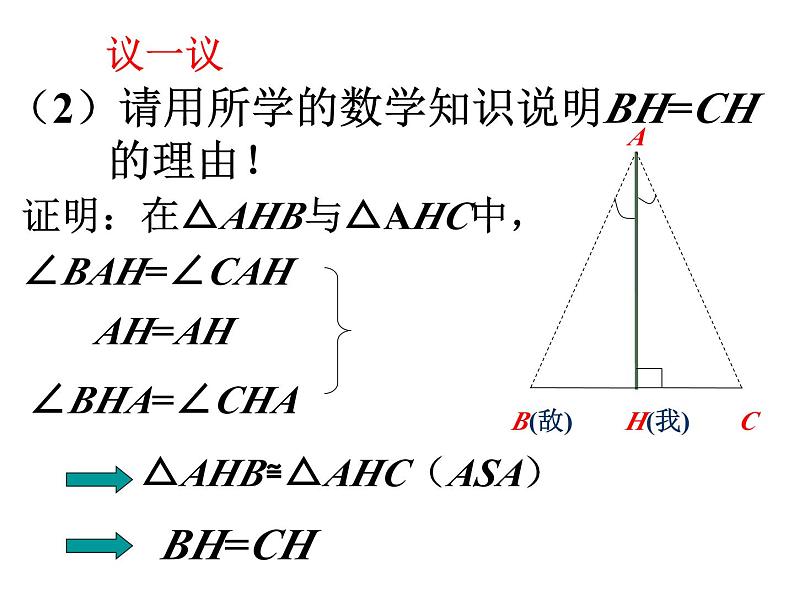

1.5 利用三角形全等测距离
展开1.5 利用三角形全等测距离复习回顾1、要证明两个三角形全等应有哪些必要条件?(1)“SSS”:三边对应相等的两个三角形全等.(2)“ASA”:两角和它们的夹边对应相等的两个三角 形全等.(3)“AAS”:两角和其中一角的对边对应相等的两个 三角形全等.(4)“SAS”:两边和它们的夹角对应相等的两个三角 形全等.在战士所讲述的方法可知:战士的身高AH不变,战士与地面是垂直的(AH⊥BC);视角∠HAC=∠HAB战士要测的是敌碉堡(B)与我军阵地(H)的距离,战士的结论是只要按要求(如图(1))测得HC的长度即可.(即BH=HC)AB(敌)CH(我)(1)战士所讲述的方法中,已知条件是什么?议一议(2)请用所学的数学知识说明BH=CH 的理由!证明:在△AHB与△AHC中,议一议方案1:方案2:方案3:2、已知:A、B两点被一个池塘隔开,无法直接测量,但两点可以到达,请你给出一个合适可行的方案,画出设计图说明依据.议一议先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.方案一方案二如图,先作三角形ABC,再找一点D,使AD∥BC,并使AD=BC,连结CD,量CD的长即得AB的长方案三如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长.所以 BA = BC补充练习设计方案:补充练习(2)运用所学有关知识设计合适可行的方案,并进行说明理由的过程(1)应用三角形全等测量距离(构造全等三角形)(3)数学知识源于生活实际,而用于实际的重大意义课内小结






