

还剩36页未读,
继续阅读
成套系列资料,整套一键下载
八年级数学上册章节重点复习考点讲义(北师大版)第3章《位置与坐标》(原卷版+解析)
展开
这是一份八年级数学上册章节重点复习考点讲义(北师大版)第3章《位置与坐标》(原卷版+解析),共39页。
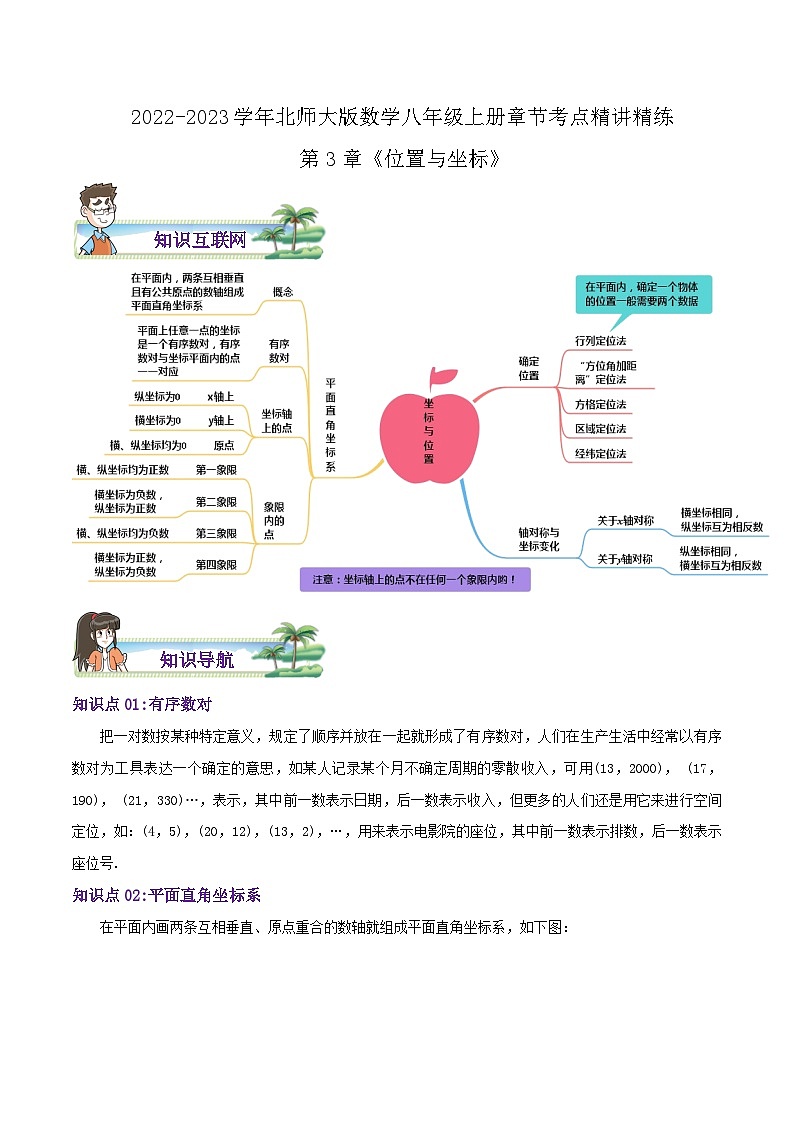
2022-2023学年北师大版数学八年级上册章节考点精讲精练第3章《位置与坐标》知识互联网知识导航知识点01:有序数对把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000), (17,190), (21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.知识点02:平面直角坐标系 在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系,如下图:细节剖析:(1)坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限,这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化.(3)要熟记坐标系中一些特殊点的坐标及特征:① x轴上的点纵坐标为零;y轴上的点横坐标为零.② 平行于x轴直线上的点横坐标不相等,纵坐标相等;平行于y轴直线上的点横坐标相等,纵坐标不相等. ③ 关于x轴对称的点横坐标相等,纵坐标互为相反数; 关于y轴对称的点纵坐标相等,横坐标互为相反数; 关于原点对称的点横、纵坐标分别互为相反数.④ 象限角平分线上的点的坐标特征: 一、三象限角平分线上的点横、纵坐标相等; 二、四象限角平分线上的点横、纵坐标互为相反数.注:反之亦成立.(4)理解坐标系中用坐标表示距离的方法和结论: ① 坐标平面内点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|. ② x轴上两点A(x1,0)、B(x2,0)的距离为AB=|x1 - x2|; y轴上两点C(0,y1)、D(0,y2)的距离为CD=|y1 - y2|.③ 平行于x轴的直线上两点A(x1,y)、B(x2,y)的距离为AB=|x1 - x2|; 平行于y轴的直线上两点C(x,y1)、D(x,y2)的距离为CD=|y1 - y2|.(5)利用坐标系求一些知道关键点坐标的几何图形的面积:切割、拼补知识点03:坐标方法的简单应用1.用坐标表示地理位置 (1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向; (2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度; (3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.细节剖析: (1)我们习惯选取向东、向北分别为x轴、y轴的正方向,建立坐标系的关键是确定原点的位置. (2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.2.用坐标表示平移 (1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).细节剖析:上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换. (2)图形的平移 在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.细节剖析:平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.考点提优练考点01:坐标与图形性质1.(2022春•海安市期中)如图,在平面直角坐标系中,三角形ABC三个顶点A、B、C的坐标A(0,4),B(﹣1,b),C(2,c),BC经过原点O,且CD⊥AB,垂足为点D,则AB•CD的值为( )A.10 B.11 C.12 D.142.(2022春•如东县期中)在下列四点中,与点(﹣3,4)所连的直线不与y轴相交的是( )A.(﹣2,3) B.(2,﹣3) C.(3,2) D.(﹣3,2)3.(2022春•鼓楼区校级期中)在平面直角坐标系中,点A(x,y),B(4,3),AB=4,且AB∥y轴,则A点的坐标为( )A.(4,7) B.(4,﹣1) C.(0,3),或(8,3) D.(4,7),或(4,﹣1)4.(2022春•朝阳区校级月考)教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,有两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4).利用以上结论解决问题:平面直角坐标系中,若E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于y轴上,且到x轴的距离是1,则4a+b的值等于 .5.(2022春•海沧区校级期末)在平面直角坐标系内,若点A(1,3),B(m2+2,3),M(2,3),N(1﹣m2,3),P(m2,3),Q(2﹣m2,3).当m>1时,则M,N,P,Q这四点中在线段AB上的点是 .6.(2022春•东莞市校级期中)已知点Q(2m﹣6,m+2),试分别根据下列条件,求出m的值并写出点Q的坐标.(1)若点Q在y轴上,求点Q的坐标.(2)若点Q在∠xOy(即第一象限)角平分线上,求点Q的坐标.7.(2022春•商南县期末)如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动(1)求点B的坐标.(2)当点P移动4秒时,请求出点P的坐标.(3)当点P移动到距离x轴5个单位长度时,求点P移动的时间.8.(2022春•海淀区期末)在平面直角坐标系xOy中,对于点A(x1,y1),点B(x2,y2),定义|x1﹣x2|+|y1﹣y2|为点A,B的“绝对距离”,记为d(A,B).特别地,当|x1﹣x2|=|y1﹣y2|时,规定d(A,B)=|x1﹣x2|,将平面内的一些点分为I,Ⅱ两类,每类至少包含两个点,记第I任意两点的绝对距离的最大值为d1,第Ⅱ类中任意两点的绝对距离的最大值为d2,称d1与d2的较大值为分类系数.如图,点A,B,C,D,E的横、纵坐标都是整数.(1)若将点A,C分为第I类,点B,D,E分为第Ⅱ类,则d1= ,d2= ,因此,这种分类方式的分类系数为 ;(2)将点A,B,C,D,E分为两类,求分类系数d的最小值:(3)点F的坐标为(m,2),已知将6个点A,B,C,D,E,F分为两类的分类系数的最小值是5,直接写出m的取值范围.考点02:两点间的距离公式9.(2022春•忠县期末)当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限10.(2022春•河西区期末)在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)11.(2023春•海淀区校级期末)A(0,a),B(3,5)是平面直角坐标系中的两点,线段AB长度的最小值为 .12.(2019春•新余期末)对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”,例如:P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P′(9,6).若点P在x轴的正半轴上,点P的“k属派生点”为点P′,且线段PP′的长度为线段OP长度的5倍,则k的值为 .13.(2023秋•射阳县校级期末)阅读下列一段文字,然后回答下列问题:已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:MN=.例如:已知P(3,1)、Q(1,﹣2),则这两点的距离PQ==.特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1﹣x2|或|y1﹣y2|.(1)已知A(1,2)、B(﹣2,﹣3),试求A、B两点间的距离;(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离;(3)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.14.(2023•张家界模拟)问题情境:在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;【应用】:(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .【拓展】:我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.解决下列问题:(1)如图2,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .15.(2023•安徽模拟)先阅读下列一段文字,在回答后面的问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.考点03:关于x轴、y轴对称的点的坐标16.(2023秋•历下区期末)已知有序数对(a,b)及常数k,我们称有序数对(ka+b,a﹣b)为有序数对(a,b)的“k阶结伴数对”.如(3,2)的“1阶结伴数”对为(1×3+2,3﹣2)即(5,1).若有序数对(a,b)(b≠0)与它的“k阶结伴数对”关于y轴对称,则此时k的值为( )A.﹣2 B.﹣ C.0 D.﹣17.(2022春•洛江区期末)点P(﹣5,3)关于x轴对称点P的坐标为( )A.(﹣5,﹣3) B.(5,3) C.(5,﹣3) D.(3,﹣5 )18.(2022•皇姑区二模)若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在第 象限.19.(2023秋•温州期末)在平面直角坐标系中,点(﹣1,2)关于y轴对称的点的坐标是 .20.(2019秋•昌平区校级期末)如图,请作出△PQR关于y轴对称的△P1Q1R1,写出它们的坐标P1 ,Q1 ,R1 21.(2016秋•天桥区期末)如图,已知△ABC的顶点坐标分别为A(﹣2,4),B(﹣6,0),C(﹣1,0).请将点A,B,C的横坐标分别乘以﹣1,纵坐标保持不变,分别得到点A′,B′,C′,并依次连接A′,B′,C′,得△A′B′C′;并求出△A′B′C′的面积.22.(2018秋•东湖区校级期中)如图,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连OB、OC.(1)判断△AOG的形状,并予以证明;(2)若点B、C关于y轴对称,求证:AO⊥BO.23.(2019秋•台山市期中)如图是一个平面直角坐标系,按要求完成下列各小题.(1)写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标;(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.考点04:坐标与图形变化-对称24.(2022•邗江区校级一模)如图,点A、B的坐标分别为(0,4)、(6,8),点P为x轴上的动点,若点B关于直线AP的对称点B'恰好落在x轴上,则点P的坐标是( )A. B. C.(2,0) D.(3,0)25.(2023秋•武城县期末)明明和乐乐下棋,明明执圆形棋子,乐乐执方形棋子,如图,棋盘中心的方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示,明明将第4枚圆形棋子放入棋盘后,所有的棋子构成轴对称图形,则明明放的位置可能是( )A.(﹣1,2) B.(﹣1,3) C.(0,2) D.(﹣1,1)26.(2023秋•丰台区期末)在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点.如图,点A的坐标为(2,4),点B的坐标为(1,1),点C为第一象限内的整点.若不共线的A,B,C三点构成轴对称图形,则点C的坐标可以是 (写出一个即可),满足题意的点C的个数为 .27.(2023秋•盐田区校级期末)欣欣和佳佳下棋,欣欣持圆形棋子,佳佳持方形棋子.若棋盘正中方形棋子的位置用(2,2)表示,右上角方形棋子的位置用(3,3)表示,要使棋盘上所有棋子组成轴对称图形,则欣欣下一枚圆形棋子的位置是 .28.(2023•黄石港区校级模拟)如图,点A坐标为(0,4),点B坐标为(4,2).直线BC垂直于y轴于点C.点D在直线BC上,点B关于直线AD的对称点在y轴上,则点D的坐标为 .29.(2023秋•江阴市期中)在平面直角坐标系xOy中,点A(2+2m,1),点B(2﹣m,4),其中m为实数,点O关于直线AB的对称点为C,则AB的最小值为 ,点P(﹣2,0)到点C的最大距离为 .30.(2022•和平区校级开学)如图,已知P(﹣2,4),M(﹣1,1),请根据每一问的要求填空:(1)写出P关于y轴的对称点Q的坐标 ,M关于y轴的对称点N的坐标 ;(2)写出P关于x=1的对称点R的坐标 ,则PR的距离为 ;(3)写出M关于x轴的对称点T的坐标 ,则NT的距离为 .31.(2023秋•峡江县期末)如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;(2)写出点A′,B′,C′的坐标.32.(2023秋•建阳区期中)如图,P,M关于直线x=1的对称点为P′,M′.(1)写出P′的坐标 ,M′的坐标 ;(2)思考,写出P(﹣2,4)关于直线x=﹣1的对称点坐标 ;写出N′(5,﹣2)关于直线x=2的对称点坐标 ;(3)思考,写出点(a,b)关于直线x=n的对称点坐标 .33.(2019秋•咸丰县期末)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长. 2022-2023学年北师大版数学八年级上册章节考点精讲精练第3章《位置与坐标》知识互联网知识导航知识点01:有序数对把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000), (17,190), (21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.知识点02:平面直角坐标系 在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系,如下图:细节剖析:(1)坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限,这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化.(3)要熟记坐标系中一些特殊点的坐标及特征:① x轴上的点纵坐标为零;y轴上的点横坐标为零.② 平行于x轴直线上的点横坐标不相等,纵坐标相等;平行于y轴直线上的点横坐标相等,纵坐标不相等. ③ 关于x轴对称的点横坐标相等,纵坐标互为相反数; 关于y轴对称的点纵坐标相等,横坐标互为相反数; 关于原点对称的点横、纵坐标分别互为相反数.④ 象限角平分线上的点的坐标特征: 一、三象限角平分线上的点横、纵坐标相等; 二、四象限角平分线上的点横、纵坐标互为相反数.注:反之亦成立.(4)理解坐标系中用坐标表示距离的方法和结论: ① 坐标平面内点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|. ② x轴上两点A(x1,0)、B(x2,0)的距离为AB=|x1 - x2|; y轴上两点C(0,y1)、D(0,y2)的距离为CD=|y1 - y2|.③ 平行于x轴的直线上两点A(x1,y)、B(x2,y)的距离为AB=|x1 - x2|; 平行于y轴的直线上两点C(x,y1)、D(x,y2)的距离为CD=|y1 - y2|.(5)利用坐标系求一些知道关键点坐标的几何图形的面积:切割、拼补知识点03:坐标方法的简单应用1.用坐标表示地理位置 (1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向; (2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度; (3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.细节剖析: (1)我们习惯选取向东、向北分别为x轴、y轴的正方向,建立坐标系的关键是确定原点的位置. (2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.2.用坐标表示平移 (1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).细节剖析:上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换. (2)图形的平移 在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.细节剖析:平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.考点提优练考点01:坐标与图形性质1.(2022春•海安市期中)如图,在平面直角坐标系中,三角形ABC三个顶点A、B、C的坐标A(0,4),B(﹣1,b),C(2,c),BC经过原点O,且CD⊥AB,垂足为点D,则AB•CD的值为( )A.10 B.11 C.12 D.14解:∵A(0,4),∴OA=4,∵B(﹣1,b),C(2,c),∴点B,C到y轴的距离分别为1,2,∵S△ABO+S△ACO=S△ABC,∴×4×1+×4×2=×AB•CD,∴AB•CD=12,故答案为:C.2.(2022春•如东县期中)在下列四点中,与点(﹣3,4)所连的直线不与y轴相交的是( )A.(﹣2,3) B.(2,﹣3) C.(3,2) D.(﹣3,2)解:点(﹣3,4)在第二象限,点(﹣3,2)也在第二象限,两点的连接线段与x轴,y轴都不相交.故选:D.3.(2022春•鼓楼区校级期中)在平面直角坐标系中,点A(x,y),B(4,3),AB=4,且AB∥y轴,则A点的坐标为( )A.(4,7) B.(4,﹣1) C.(0,3),或(8,3) D.(4,7),或(4,﹣1)解:∵AB∥y轴,∴A、B两点的横坐标相同,又∵AB=4,∴B点纵坐标为:3+4=7或3﹣4=﹣1,∴B点的坐标为:(4,7)或(4,﹣1).故选:D.4.(2022春•朝阳区校级月考)教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,有两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4).利用以上结论解决问题:平面直角坐标系中,若E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于y轴上,且到x轴的距离是1,则4a+b的值等于 4或0 .解:根据题意得:G(,),∵线段EF的中点G恰好位于y轴上,且到x轴的距离是1,∴,解得:4a+b=4或0.故答案为:4或0.5.(2022春•海沧区校级期末)在平面直角坐标系内,若点A(1,3),B(m2+2,3),M(2,3),N(1﹣m2,3),P(m2,3),Q(2﹣m2,3).当m>1时,则M,N,P,Q这四点中在线段AB上的点是 M,P .解:∵这六个点的纵坐标都是3,∴它们都在直线AB上,与x轴平行,∵m>1,∴m2>1,∴1<2<m2+2,1﹣m2<0,1<m2<m2+2,2﹣m2<1,∴M,N,P,Q这四点中在线段AB上的点是M,P.故答案为:M,P.6.(2022春•东莞市校级期中)已知点Q(2m﹣6,m+2),试分别根据下列条件,求出m的值并写出点Q的坐标.(1)若点Q在y轴上,求点Q的坐标.(2)若点Q在∠xOy(即第一象限)角平分线上,求点Q的坐标.解:(1)点Q在y轴上,则2m﹣6=0,解得m=3.所以m+2=5,故Q点的坐标是(0,5);(2)当点Q在∠xOy(即第一象限)角平分线上,有2m﹣6=m+2,解得m=8.所以2m﹣6=10.故Q点的坐标是(10,10).7.(2022春•商南县期末)如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动(1)求点B的坐标.(2)当点P移动4秒时,请求出点P的坐标.(3)当点P移动到距离x轴5个单位长度时,求点P移动的时间.解:(1)∵a、b满足+|b﹣6|=0,∴a﹣4=0,b﹣6=0,解得a=4,b=6,∴点B的坐标是(4,6);(2)∵点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动,∴点P的路程:2×4=8,∵OA=4,OC=6,∴当点P移动4秒时,在线段AB上,AP=8﹣4=4,即当点P移动4秒时,此时点P的坐标是(4,4);(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况,第一种情况,当点P在OC上时,点P移动的时间是:[2(4+6)﹣5]÷2=7.5(秒),第二种情况,当点P在BA上时.点P移动的时间是:(5+4)÷2=4.5(秒),故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是4.5秒或7.5秒.8.(2022春•海淀区期末)在平面直角坐标系xOy中,对于点A(x1,y1),点B(x2,y2),定义|x1﹣x2|+|y1﹣y2|为点A,B的“绝对距离”,记为d(A,B).特别地,当|x1﹣x2|=|y1﹣y2|时,规定d(A,B)=|x1﹣x2|,将平面内的一些点分为I,Ⅱ两类,每类至少包含两个点,记第I任意两点的绝对距离的最大值为d1,第Ⅱ类中任意两点的绝对距离的最大值为d2,称d1与d2的较大值为分类系数.如图,点A,B,C,D,E的横、纵坐标都是整数.(1)若将点A,C分为第I类,点B,D,E分为第Ⅱ类,则d1= 2 ,d2= 5 ,因此,这种分类方式的分类系数为 5 ;(2)将点A,B,C,D,E分为两类,求分类系数d的最小值:(3)点F的坐标为(m,2),已知将6个点A,B,C,D,E,F分为两类的分类系数的最小值是5,直接写出m的取值范围.解:(1)观察坐标图,根据题意得知:d1=d(A,C)=|xA﹣xC|=2;d2=d(B,E)=|yB﹣yE|=5;因为d2>d1,所以分类系数为5;故答案为:2;5;5;(2)共有十种分类方法:若将点A,B分为第I类,点C,D,E分为第Ⅱ类:d1=d(A,B)=|yA﹣yB|=4,d2=d(D,E)=|yD﹣yE|=3,因为 d1>d2,所以分类系数为4;若将点A,C分为第I类,点B,D,E分为第Ⅱ类:分类系数为5;若将点A,D分为第I类,点B,C,E分为第Ⅱ类:d1=d(A,D)=|xA﹣xD|=3,d2=d(B,E)=|yB﹣yE|=5,因为d2>d1,所以分类系数为5;若将点A,E分为第I类,点B,C,D分为第Ⅱ类:d1=d(A,E)=|xA﹣xE|=4,d2=d(B,C)=|yB﹣yC|=4,因为d1=d2,所以分类系数为4;若将点B,C分为第I类,点A,D,E分为第Ⅱ类:d1=d(B,C)=|yB﹣yC|=4,d2=d(A,E)=|xA﹣xE|=4,因为d1=d2,所以分类系数为4;若将点B,D分为第I类,点A,C,E分为第Ⅱ类:d1=d(B,D)=|xB﹣xD|=2,d2=d(A,E)=|xA﹣xE|=4,因为d2>d1,所以分类系数为4;若将点B,E分为第I类,点A,C,D分为第Ⅱ类:d1=d(B,E)=|yB﹣yE|=5,d2=d(A,D)=|xA﹣xD|=3,因为d1>d2,所以分类系数为5;若将点C,D分为第I类,点A,B,E分为第Ⅱ类:d1=d(C,D)=|yC﹣yD|=2,d2=d(B,E)=|yB﹣yE|=5,因为d2>d1,所以分类系数为5;若将点C,E分为第I类,点A,B,D分为第Ⅱ类:d1=d(C,E)=|xC﹣xE|=2,d2=d(A,B)=|yA﹣yB|=4,因为d2>d1,所以分类系数为4;若将点D,E分为第I类,点A,B,C分为第Ⅱ类:d1=d(D,E)=|yD﹣yE|=3,d2=d(A,B)=|yA﹣yB|=4,因为d2>d1,所以分类系数为4;比较得:分类系数d的最小值为4;(3)当点F在点E的右边时,|xF﹣xA|≤5,m﹣1≤5;当点F在点A的左边时,|xF﹣xE|≤5,5﹣m≤5,得0≤m≤6.故m的取值范围是:0≤m≤6.考点02:两点间的距离公式9.(2022春•忠县期末)当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限解:根据题意得AB==,∵(x+1)2≥0,(2y+2)2≥0,∴当x+1=0,2y+2=0时,AB最小,解得x=﹣1,y=﹣1,∴点P的坐标为(﹣1,﹣1),∴P点在第三象限.故选:C.10.(2022春•河西区期末)在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)解:依题意可得:∵AC∥x轴,A(﹣3,2)∴y=2,根据垂线段最短,当BC⊥AC于点C时,点B到AC的距离最短,即BC的最小值=5﹣2=3,此时点C的坐标为(3,2),故选:D.11.(2023春•海淀区校级期末)A(0,a),B(3,5)是平面直角坐标系中的两点,线段AB长度的最小值为 3 .解:如图.∵A(0,a),∴A在y轴上.∴线段AB的长度为B点到y轴上点的距离.若使得线段AB长度的最小,由垂线段最短,∴当A在(0,5)时,即AB⊥y轴,线段AB长度最小.∴(dAB)min=3.故答案为:3.12.(2019春•新余期末)对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”,例如:P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P′(9,6).若点P在x轴的正半轴上,点P的“k属派生点”为点P′,且线段PP′的长度为线段OP长度的5倍,则k的值为 ±5 .解:设P(m,0)(m>0),由题意:P′(m,mk),∵PP′=5OP,∴|mk|=5m,∵m>0,∴|k|=5,∴k=±5.故答案为:±5.13.(2023秋•射阳县校级期末)阅读下列一段文字,然后回答下列问题:已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:MN=.例如:已知P(3,1)、Q(1,﹣2),则这两点的距离PQ==.特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1﹣x2|或|y1﹣y2|.(1)已知A(1,2)、B(﹣2,﹣3),试求A、B两点间的距离;(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离;(3)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.解:(1)AB==;(2)AB=5﹣(﹣1)=6;(3)△ABC为直角三角形.理由如下:∵AB==,AC==2,BC==5,∴AB2+AC2=BC2,∴△ABC为直角三角形.14.(2023•张家界模拟)问题情境:在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;【应用】:(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 3 .(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 (1,2)或(1,﹣2) .【拓展】:我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.解决下列问题:(1)如图2,已知E(2,0),若F(﹣1,﹣2),则d(E,F) =5 ;(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= 2或﹣2 .(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= 4或8 .解:【应用】:(1)AB的长度为|﹣1﹣2|=3.故答案为:3.(2)由CD∥y轴,可设点D的坐标为(1,m),∵CD=2,∴|0﹣m|=2,解得:m=±2,∴点D的坐标为(1,2)或(1,﹣2).故答案为:(1,2)或(1,﹣2).【拓展】:(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.故答案为:=5.(2)∵E(2,0),H(1,t),d(E,H)=3,∴|2﹣1|+|0﹣t|=3,解得:t=±2.故答案为:2或﹣2.(3)由点Q在x轴上,可设点Q的坐标为(x,0),∵三角形OPQ的面积为3,∴|x|×3=3,解得:x=±2.当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.故答案为:4或8.15.(2023•安徽模拟)先阅读下列一段文字,在回答后面的问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.解:(1)∵A(2,4)、B(﹣3,﹣8),∴|AB|==13,即A、B两点间的距离是13;(2)∵A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,∴|AB|=|﹣1﹣5|=6,即A、B两点间的距离是6;(3)△ABC是等腰三角形,理由如下:∵一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),∴AB=5,BC=6,AC=5,∴AB=AC,∴△ABC是等腰三角形.考点03:关于x轴、y轴对称的点的坐标16.(2023秋•历下区期末)已知有序数对(a,b)及常数k,我们称有序数对(ka+b,a﹣b)为有序数对(a,b)的“k阶结伴数对”.如(3,2)的“1阶结伴数”对为(1×3+2,3﹣2)即(5,1).若有序数对(a,b)(b≠0)与它的“k阶结伴数对”关于y轴对称,则此时k的值为( )A.﹣2 B.﹣ C.0 D.﹣解:有序数对(a,b)(b≠0)它的“k阶结伴数对”为(ka+b,a﹣b),∵(a,b)与(ka+b,a﹣b)关于y轴对称,∴a=﹣ka﹣b,b=a﹣b,解得k=﹣,故选:B.17.(2022春•洛江区期末)点P(﹣5,3)关于x轴对称点P的坐标为( )A.(﹣5,﹣3) B.(5,3) C.(5,﹣3) D.(3,﹣5 )解:点P(﹣5,3)关于x轴对称点P的坐标为(﹣5,﹣3),故选:A.18.(2022•皇姑区二模)若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在第 四 象限.解:由题意,得a﹣2=1,b+5=3,解得a=3,b=﹣2,点C(a,b)在第四象限,故答案为:四.19.(2023秋•温州期末)在平面直角坐标系中,点(﹣1,2)关于y轴对称的点的坐标是 (1,2) .解:由点(﹣1,2)关于y轴对称的点的坐标是(1,2).故答案为:(1,2).20.(2019秋•昌平区校级期末)如图,请作出△PQR关于y轴对称的△P1Q1R1,写出它们的坐标P1 (4,﹣1) ,Q1 (1,4) ,R1 (﹣1,1) 解:如图,△P1Q1R1即为所求.观察图象可知:P1(4,﹣1)、Q1(1,4)、R1(﹣1,1),故答案为(4,﹣1),(1,4),(﹣1,1).21.(2016秋•天桥区期末)如图,已知△ABC的顶点坐标分别为A(﹣2,4),B(﹣6,0),C(﹣1,0).请将点A,B,C的横坐标分别乘以﹣1,纵坐标保持不变,分别得到点A′,B′,C′,并依次连接A′,B′,C′,得△A′B′C′;并求出△A′B′C′的面积.解:如图所示,△A′B′C′即为所求,△A′B′C′的面积为×5×4=10.22.(2018秋•东湖区校级期中)如图,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连OB、OC.(1)判断△AOG的形状,并予以证明;(2)若点B、C关于y轴对称,求证:AO⊥BO.解:(1)△AOG是等腰三角形;证明:∵AC∥y轴,∴∠CAO=∠AOG,∵AO平分∠BAC,∴∠CAO=∠GAO,∴∠GAO=∠AOG,∴AG=GO,∴△AOG是等腰三角形;(2)证明:连接BC交y轴于K,过A作AN⊥y轴于N,∵AC∥y轴,点B、C关于y轴对称,∴AN=CK=BK,在△ANG和△BKG中,,∴△ANG≌△BKG,(AAS)∴AG=BG,∵AG=OG,(1)中已证,∴AG=OG=BG,∴∠BOG=∠OBG,∠OAG=∠AOG,∵∠OAG+∠AOG+∠BOG+∠OBG=180°,∴∠AOG+∠BOG=90°,∴AO⊥BO.23.(2019秋•台山市期中)如图是一个平面直角坐标系,按要求完成下列各小题.(1)写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标;(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.解:(1)点A的坐标为(﹣2,0),点B的坐标为(0,﹣3),点D的坐标为(4,0),点F的坐标为(0,3);(2)点B与点C的纵坐标相等,线段BC平行于x轴;(3)点E关于y轴的对称点的坐标为(﹣3,3),它与点C关于原点对称.考点04:坐标与图形变化-对称24.(2022•邗江区校级一模)如图,点A、B的坐标分别为(0,4)、(6,8),点P为x轴上的动点,若点B关于直线AP的对称点B'恰好落在x轴上,则点P的坐标是( )A. B. C.(2,0) D.(3,0)解:如图,连接AB、AB′,∵A(0,4),B(6,8),∴AB==2,∵点B与B′关于直线AP对称,∴AB′=AB=2,在Rt△AOB′中,B′O===6,∴B′点坐标为(﹣6,0)或(6,0),∵A(0,4),点B(6,8)关于直线AP的对称点B′恰好落在x轴上,∴点B(6,8)关于直线AP的对称点B′(﹣6,0),∴B′点坐标为(6,0)不合题意舍去,设直线BB′方程为y=kx+b将B(6,8),B′(﹣6,0)代入得,解得k=,b=4,∴直线BB′的解析式为:y=x+4,∴直线AP的解析式为:y=﹣x+4,当yAP=0时,﹣x+4=0,解得:x=,∴点P的坐标为:(,0);故选:A.25.(2023秋•武城县期末)明明和乐乐下棋,明明执圆形棋子,乐乐执方形棋子,如图,棋盘中心的方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示,明明将第4枚圆形棋子放入棋盘后,所有的棋子构成轴对称图形,则明明放的位置可能是( )A.(﹣1,2) B.(﹣1,3) C.(0,2) D.(﹣1,1)解:将第4枚圆形放在中心方形棋子的正上方一格处,即(﹣1,1)处,构成以过点(﹣1,0),(0,﹣1)的直线为对称轴的轴对称图形.故选:D.26.(2023秋•丰台区期末)在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点.如图,点A的坐标为(2,4),点B的坐标为(1,1),点C为第一象限内的整点.若不共线的A,B,C三点构成轴对称图形,则点C的坐标可以是 (3.1)(答案不唯一) (写出一个即可),满足题意的点C的个数为 6 .解:由不共线的A,B,C三点构成轴对称图形,则△ABC是等腰三角形,如图,共有符合要求的点C有6个.其中点C坐标为(3,1)(答案不唯一),故答案为:(3,1)(不唯一),6.27.(2023秋•盐田区校级期末)欣欣和佳佳下棋,欣欣持圆形棋子,佳佳持方形棋子.若棋盘正中方形棋子的位置用(2,2)表示,右上角方形棋子的位置用(3,3)表示,要使棋盘上所有棋子组成轴对称图形,则欣欣下一枚圆形棋子的位置是 (2,1) .解:第八枚圆形棋子放在位置,如图所示,坐标为(2,1).故答案为:(2,1).28.(2023•黄石港区校级模拟)如图,点A坐标为(0,4),点B坐标为(4,2).直线BC垂直于y轴于点C.点D在直线BC上,点B关于直线AD的对称点在y轴上,则点D的坐标为 (﹣1,2)或(﹣﹣1,2) .解:∵点A坐标为(0,4),点B坐标为(4,2),∴AB==2,∵由题意点D在∠CAB的角平分线或∠CAB的外角平分线上,作DH⊥AB于H.∵DC⊥AC,DH⊥AB,AD平分∠BAC,∴DC=DH,设DC=DH=m,则有•AC•BC=•AC•DC+•AB•DH,∴2×4=2m+2m,∴m=﹣1,∴D(﹣1,2),当D′在∠CAB的外角平分线上时,同法可得CD′=+1,∴D′(﹣﹣1,2)故答案为:(﹣1,2)或(﹣﹣1,2).29.(2023秋•江阴市期中)在平面直角坐标系xOy中,点A(2+2m,1),点B(2﹣m,4),其中m为实数,点O关于直线AB的对称点为C,则AB的最小值为 3 ,点P(﹣2,0)到点C的最大距离为 5+ .解:∵A(2+2m,1),点B(2﹣m,4),∴点A在直线y=1上,点B在直线y=4上,∴AB的最小值为3,如图,设直线AB的解析式为y=kx+b.则有,解得,∴直线AB的解析式为y=﹣•x+3+,∵x=2时,y=3,∴直线AB经过定点D(2,3),连接PD,CD,OD,∵P(﹣2,0),∵PD==5,OD==,∵O,C关于直线AB对称,∴DC=OD=,∴PC≤PD+CD=5+,∴PC的最大值为5+.故答案为:3,5+.30.(2022•和平区校级开学)如图,已知P(﹣2,4),M(﹣1,1),请根据每一问的要求填空:(1)写出P关于y轴的对称点Q的坐标 (2,4) ,M关于y轴的对称点N的坐标 (1,1) ;(2)写出P关于x=1的对称点R的坐标 (4,4) ,则PR的距离为 6 ;(3)写出M关于x轴的对称点T的坐标 (﹣1,﹣1) ,则NT的距离为 2 .解:(1)如图,点Q,点N即为所求,Q(2,4),N(1,1).故答案为:(2,4),(1,1);(2)如图,点R即为所求,R(4,4),PR=6.故答案为:(4,4),6;(3)如图,点T即为所求.T(﹣1,﹣1),NT==2.故答案为:(﹣1,﹣1),2.31.(2023秋•峡江县期末)如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;(2)写出点A′,B′,C′的坐标.解:(1)如图,(2)点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1).32.(2023秋•建阳区期中)如图,P,M关于直线x=1的对称点为P′,M′.(1)写出P′的坐标 (4,4) ,M′的坐标 (3,1) ;(2)思考,写出P(﹣2,4)关于直线x=﹣1的对称点坐标 (0,4) ;写出N′(5,﹣2)关于直线x=2的对称点坐标 (﹣1,﹣2) ;(3)思考,写出点(a,b)关于直线x=n的对称点坐标 (2n﹣a,b) .解:(1)由题意,P′(4,4),M′(3,1),故答案为:(4,4),(3,1);(2)P(﹣2,4)关于直线x=﹣1的对称点坐标(0,4);N′(5,﹣2)关于直线x=2的对称点坐标(﹣1,﹣2).故答案为:(0,4),(﹣1,﹣2);(3)设对称点坐标为(x,y),则有=n,y=b,x=2n﹣a,∴点(a,b)关于直线x=n的对称点坐标(2n﹣a,b).故答案为:(2n﹣a,b).33.(2019秋•咸丰县期末)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);(2)如图1,当0<a<3时,∵P与P1关于y轴对称,P(﹣a,0),∴P1(a,0),又∵P1与P2关于l:直线x=3对称,设P2(x,0),可得:=3,即x=6﹣a,∴P2(6﹣a,0),则PP2=6﹣a﹣(﹣a)=6﹣a+a=6.
2022-2023学年北师大版数学八年级上册章节考点精讲精练第3章《位置与坐标》知识互联网知识导航知识点01:有序数对把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000), (17,190), (21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.知识点02:平面直角坐标系 在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系,如下图:细节剖析:(1)坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限,这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化.(3)要熟记坐标系中一些特殊点的坐标及特征:① x轴上的点纵坐标为零;y轴上的点横坐标为零.② 平行于x轴直线上的点横坐标不相等,纵坐标相等;平行于y轴直线上的点横坐标相等,纵坐标不相等. ③ 关于x轴对称的点横坐标相等,纵坐标互为相反数; 关于y轴对称的点纵坐标相等,横坐标互为相反数; 关于原点对称的点横、纵坐标分别互为相反数.④ 象限角平分线上的点的坐标特征: 一、三象限角平分线上的点横、纵坐标相等; 二、四象限角平分线上的点横、纵坐标互为相反数.注:反之亦成立.(4)理解坐标系中用坐标表示距离的方法和结论: ① 坐标平面内点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|. ② x轴上两点A(x1,0)、B(x2,0)的距离为AB=|x1 - x2|; y轴上两点C(0,y1)、D(0,y2)的距离为CD=|y1 - y2|.③ 平行于x轴的直线上两点A(x1,y)、B(x2,y)的距离为AB=|x1 - x2|; 平行于y轴的直线上两点C(x,y1)、D(x,y2)的距离为CD=|y1 - y2|.(5)利用坐标系求一些知道关键点坐标的几何图形的面积:切割、拼补知识点03:坐标方法的简单应用1.用坐标表示地理位置 (1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向; (2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度; (3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.细节剖析: (1)我们习惯选取向东、向北分别为x轴、y轴的正方向,建立坐标系的关键是确定原点的位置. (2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.2.用坐标表示平移 (1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).细节剖析:上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换. (2)图形的平移 在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.细节剖析:平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.考点提优练考点01:坐标与图形性质1.(2022春•海安市期中)如图,在平面直角坐标系中,三角形ABC三个顶点A、B、C的坐标A(0,4),B(﹣1,b),C(2,c),BC经过原点O,且CD⊥AB,垂足为点D,则AB•CD的值为( )A.10 B.11 C.12 D.142.(2022春•如东县期中)在下列四点中,与点(﹣3,4)所连的直线不与y轴相交的是( )A.(﹣2,3) B.(2,﹣3) C.(3,2) D.(﹣3,2)3.(2022春•鼓楼区校级期中)在平面直角坐标系中,点A(x,y),B(4,3),AB=4,且AB∥y轴,则A点的坐标为( )A.(4,7) B.(4,﹣1) C.(0,3),或(8,3) D.(4,7),或(4,﹣1)4.(2022春•朝阳区校级月考)教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,有两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4).利用以上结论解决问题:平面直角坐标系中,若E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于y轴上,且到x轴的距离是1,则4a+b的值等于 .5.(2022春•海沧区校级期末)在平面直角坐标系内,若点A(1,3),B(m2+2,3),M(2,3),N(1﹣m2,3),P(m2,3),Q(2﹣m2,3).当m>1时,则M,N,P,Q这四点中在线段AB上的点是 .6.(2022春•东莞市校级期中)已知点Q(2m﹣6,m+2),试分别根据下列条件,求出m的值并写出点Q的坐标.(1)若点Q在y轴上,求点Q的坐标.(2)若点Q在∠xOy(即第一象限)角平分线上,求点Q的坐标.7.(2022春•商南县期末)如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动(1)求点B的坐标.(2)当点P移动4秒时,请求出点P的坐标.(3)当点P移动到距离x轴5个单位长度时,求点P移动的时间.8.(2022春•海淀区期末)在平面直角坐标系xOy中,对于点A(x1,y1),点B(x2,y2),定义|x1﹣x2|+|y1﹣y2|为点A,B的“绝对距离”,记为d(A,B).特别地,当|x1﹣x2|=|y1﹣y2|时,规定d(A,B)=|x1﹣x2|,将平面内的一些点分为I,Ⅱ两类,每类至少包含两个点,记第I任意两点的绝对距离的最大值为d1,第Ⅱ类中任意两点的绝对距离的最大值为d2,称d1与d2的较大值为分类系数.如图,点A,B,C,D,E的横、纵坐标都是整数.(1)若将点A,C分为第I类,点B,D,E分为第Ⅱ类,则d1= ,d2= ,因此,这种分类方式的分类系数为 ;(2)将点A,B,C,D,E分为两类,求分类系数d的最小值:(3)点F的坐标为(m,2),已知将6个点A,B,C,D,E,F分为两类的分类系数的最小值是5,直接写出m的取值范围.考点02:两点间的距离公式9.(2022春•忠县期末)当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限10.(2022春•河西区期末)在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)11.(2023春•海淀区校级期末)A(0,a),B(3,5)是平面直角坐标系中的两点,线段AB长度的最小值为 .12.(2019春•新余期末)对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”,例如:P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P′(9,6).若点P在x轴的正半轴上,点P的“k属派生点”为点P′,且线段PP′的长度为线段OP长度的5倍,则k的值为 .13.(2023秋•射阳县校级期末)阅读下列一段文字,然后回答下列问题:已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:MN=.例如:已知P(3,1)、Q(1,﹣2),则这两点的距离PQ==.特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1﹣x2|或|y1﹣y2|.(1)已知A(1,2)、B(﹣2,﹣3),试求A、B两点间的距离;(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离;(3)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.14.(2023•张家界模拟)问题情境:在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;【应用】:(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .【拓展】:我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.解决下列问题:(1)如图2,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .15.(2023•安徽模拟)先阅读下列一段文字,在回答后面的问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.考点03:关于x轴、y轴对称的点的坐标16.(2023秋•历下区期末)已知有序数对(a,b)及常数k,我们称有序数对(ka+b,a﹣b)为有序数对(a,b)的“k阶结伴数对”.如(3,2)的“1阶结伴数”对为(1×3+2,3﹣2)即(5,1).若有序数对(a,b)(b≠0)与它的“k阶结伴数对”关于y轴对称,则此时k的值为( )A.﹣2 B.﹣ C.0 D.﹣17.(2022春•洛江区期末)点P(﹣5,3)关于x轴对称点P的坐标为( )A.(﹣5,﹣3) B.(5,3) C.(5,﹣3) D.(3,﹣5 )18.(2022•皇姑区二模)若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在第 象限.19.(2023秋•温州期末)在平面直角坐标系中,点(﹣1,2)关于y轴对称的点的坐标是 .20.(2019秋•昌平区校级期末)如图,请作出△PQR关于y轴对称的△P1Q1R1,写出它们的坐标P1 ,Q1 ,R1 21.(2016秋•天桥区期末)如图,已知△ABC的顶点坐标分别为A(﹣2,4),B(﹣6,0),C(﹣1,0).请将点A,B,C的横坐标分别乘以﹣1,纵坐标保持不变,分别得到点A′,B′,C′,并依次连接A′,B′,C′,得△A′B′C′;并求出△A′B′C′的面积.22.(2018秋•东湖区校级期中)如图,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连OB、OC.(1)判断△AOG的形状,并予以证明;(2)若点B、C关于y轴对称,求证:AO⊥BO.23.(2019秋•台山市期中)如图是一个平面直角坐标系,按要求完成下列各小题.(1)写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标;(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.考点04:坐标与图形变化-对称24.(2022•邗江区校级一模)如图,点A、B的坐标分别为(0,4)、(6,8),点P为x轴上的动点,若点B关于直线AP的对称点B'恰好落在x轴上,则点P的坐标是( )A. B. C.(2,0) D.(3,0)25.(2023秋•武城县期末)明明和乐乐下棋,明明执圆形棋子,乐乐执方形棋子,如图,棋盘中心的方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示,明明将第4枚圆形棋子放入棋盘后,所有的棋子构成轴对称图形,则明明放的位置可能是( )A.(﹣1,2) B.(﹣1,3) C.(0,2) D.(﹣1,1)26.(2023秋•丰台区期末)在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点.如图,点A的坐标为(2,4),点B的坐标为(1,1),点C为第一象限内的整点.若不共线的A,B,C三点构成轴对称图形,则点C的坐标可以是 (写出一个即可),满足题意的点C的个数为 .27.(2023秋•盐田区校级期末)欣欣和佳佳下棋,欣欣持圆形棋子,佳佳持方形棋子.若棋盘正中方形棋子的位置用(2,2)表示,右上角方形棋子的位置用(3,3)表示,要使棋盘上所有棋子组成轴对称图形,则欣欣下一枚圆形棋子的位置是 .28.(2023•黄石港区校级模拟)如图,点A坐标为(0,4),点B坐标为(4,2).直线BC垂直于y轴于点C.点D在直线BC上,点B关于直线AD的对称点在y轴上,则点D的坐标为 .29.(2023秋•江阴市期中)在平面直角坐标系xOy中,点A(2+2m,1),点B(2﹣m,4),其中m为实数,点O关于直线AB的对称点为C,则AB的最小值为 ,点P(﹣2,0)到点C的最大距离为 .30.(2022•和平区校级开学)如图,已知P(﹣2,4),M(﹣1,1),请根据每一问的要求填空:(1)写出P关于y轴的对称点Q的坐标 ,M关于y轴的对称点N的坐标 ;(2)写出P关于x=1的对称点R的坐标 ,则PR的距离为 ;(3)写出M关于x轴的对称点T的坐标 ,则NT的距离为 .31.(2023秋•峡江县期末)如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;(2)写出点A′,B′,C′的坐标.32.(2023秋•建阳区期中)如图,P,M关于直线x=1的对称点为P′,M′.(1)写出P′的坐标 ,M′的坐标 ;(2)思考,写出P(﹣2,4)关于直线x=﹣1的对称点坐标 ;写出N′(5,﹣2)关于直线x=2的对称点坐标 ;(3)思考,写出点(a,b)关于直线x=n的对称点坐标 .33.(2019秋•咸丰县期末)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长. 2022-2023学年北师大版数学八年级上册章节考点精讲精练第3章《位置与坐标》知识互联网知识导航知识点01:有序数对把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000), (17,190), (21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.知识点02:平面直角坐标系 在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系,如下图:细节剖析:(1)坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限,这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化.(3)要熟记坐标系中一些特殊点的坐标及特征:① x轴上的点纵坐标为零;y轴上的点横坐标为零.② 平行于x轴直线上的点横坐标不相等,纵坐标相等;平行于y轴直线上的点横坐标相等,纵坐标不相等. ③ 关于x轴对称的点横坐标相等,纵坐标互为相反数; 关于y轴对称的点纵坐标相等,横坐标互为相反数; 关于原点对称的点横、纵坐标分别互为相反数.④ 象限角平分线上的点的坐标特征: 一、三象限角平分线上的点横、纵坐标相等; 二、四象限角平分线上的点横、纵坐标互为相反数.注:反之亦成立.(4)理解坐标系中用坐标表示距离的方法和结论: ① 坐标平面内点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|. ② x轴上两点A(x1,0)、B(x2,0)的距离为AB=|x1 - x2|; y轴上两点C(0,y1)、D(0,y2)的距离为CD=|y1 - y2|.③ 平行于x轴的直线上两点A(x1,y)、B(x2,y)的距离为AB=|x1 - x2|; 平行于y轴的直线上两点C(x,y1)、D(x,y2)的距离为CD=|y1 - y2|.(5)利用坐标系求一些知道关键点坐标的几何图形的面积:切割、拼补知识点03:坐标方法的简单应用1.用坐标表示地理位置 (1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向; (2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度; (3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.细节剖析: (1)我们习惯选取向东、向北分别为x轴、y轴的正方向,建立坐标系的关键是确定原点的位置. (2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.2.用坐标表示平移 (1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).细节剖析:上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换. (2)图形的平移 在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.细节剖析:平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.考点提优练考点01:坐标与图形性质1.(2022春•海安市期中)如图,在平面直角坐标系中,三角形ABC三个顶点A、B、C的坐标A(0,4),B(﹣1,b),C(2,c),BC经过原点O,且CD⊥AB,垂足为点D,则AB•CD的值为( )A.10 B.11 C.12 D.14解:∵A(0,4),∴OA=4,∵B(﹣1,b),C(2,c),∴点B,C到y轴的距离分别为1,2,∵S△ABO+S△ACO=S△ABC,∴×4×1+×4×2=×AB•CD,∴AB•CD=12,故答案为:C.2.(2022春•如东县期中)在下列四点中,与点(﹣3,4)所连的直线不与y轴相交的是( )A.(﹣2,3) B.(2,﹣3) C.(3,2) D.(﹣3,2)解:点(﹣3,4)在第二象限,点(﹣3,2)也在第二象限,两点的连接线段与x轴,y轴都不相交.故选:D.3.(2022春•鼓楼区校级期中)在平面直角坐标系中,点A(x,y),B(4,3),AB=4,且AB∥y轴,则A点的坐标为( )A.(4,7) B.(4,﹣1) C.(0,3),或(8,3) D.(4,7),或(4,﹣1)解:∵AB∥y轴,∴A、B两点的横坐标相同,又∵AB=4,∴B点纵坐标为:3+4=7或3﹣4=﹣1,∴B点的坐标为:(4,7)或(4,﹣1).故选:D.4.(2022春•朝阳区校级月考)教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,有两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4).利用以上结论解决问题:平面直角坐标系中,若E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于y轴上,且到x轴的距离是1,则4a+b的值等于 4或0 .解:根据题意得:G(,),∵线段EF的中点G恰好位于y轴上,且到x轴的距离是1,∴,解得:4a+b=4或0.故答案为:4或0.5.(2022春•海沧区校级期末)在平面直角坐标系内,若点A(1,3),B(m2+2,3),M(2,3),N(1﹣m2,3),P(m2,3),Q(2﹣m2,3).当m>1时,则M,N,P,Q这四点中在线段AB上的点是 M,P .解:∵这六个点的纵坐标都是3,∴它们都在直线AB上,与x轴平行,∵m>1,∴m2>1,∴1<2<m2+2,1﹣m2<0,1<m2<m2+2,2﹣m2<1,∴M,N,P,Q这四点中在线段AB上的点是M,P.故答案为:M,P.6.(2022春•东莞市校级期中)已知点Q(2m﹣6,m+2),试分别根据下列条件,求出m的值并写出点Q的坐标.(1)若点Q在y轴上,求点Q的坐标.(2)若点Q在∠xOy(即第一象限)角平分线上,求点Q的坐标.解:(1)点Q在y轴上,则2m﹣6=0,解得m=3.所以m+2=5,故Q点的坐标是(0,5);(2)当点Q在∠xOy(即第一象限)角平分线上,有2m﹣6=m+2,解得m=8.所以2m﹣6=10.故Q点的坐标是(10,10).7.(2022春•商南县期末)如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动(1)求点B的坐标.(2)当点P移动4秒时,请求出点P的坐标.(3)当点P移动到距离x轴5个单位长度时,求点P移动的时间.解:(1)∵a、b满足+|b﹣6|=0,∴a﹣4=0,b﹣6=0,解得a=4,b=6,∴点B的坐标是(4,6);(2)∵点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动,∴点P的路程:2×4=8,∵OA=4,OC=6,∴当点P移动4秒时,在线段AB上,AP=8﹣4=4,即当点P移动4秒时,此时点P的坐标是(4,4);(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况,第一种情况,当点P在OC上时,点P移动的时间是:[2(4+6)﹣5]÷2=7.5(秒),第二种情况,当点P在BA上时.点P移动的时间是:(5+4)÷2=4.5(秒),故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是4.5秒或7.5秒.8.(2022春•海淀区期末)在平面直角坐标系xOy中,对于点A(x1,y1),点B(x2,y2),定义|x1﹣x2|+|y1﹣y2|为点A,B的“绝对距离”,记为d(A,B).特别地,当|x1﹣x2|=|y1﹣y2|时,规定d(A,B)=|x1﹣x2|,将平面内的一些点分为I,Ⅱ两类,每类至少包含两个点,记第I任意两点的绝对距离的最大值为d1,第Ⅱ类中任意两点的绝对距离的最大值为d2,称d1与d2的较大值为分类系数.如图,点A,B,C,D,E的横、纵坐标都是整数.(1)若将点A,C分为第I类,点B,D,E分为第Ⅱ类,则d1= 2 ,d2= 5 ,因此,这种分类方式的分类系数为 5 ;(2)将点A,B,C,D,E分为两类,求分类系数d的最小值:(3)点F的坐标为(m,2),已知将6个点A,B,C,D,E,F分为两类的分类系数的最小值是5,直接写出m的取值范围.解:(1)观察坐标图,根据题意得知:d1=d(A,C)=|xA﹣xC|=2;d2=d(B,E)=|yB﹣yE|=5;因为d2>d1,所以分类系数为5;故答案为:2;5;5;(2)共有十种分类方法:若将点A,B分为第I类,点C,D,E分为第Ⅱ类:d1=d(A,B)=|yA﹣yB|=4,d2=d(D,E)=|yD﹣yE|=3,因为 d1>d2,所以分类系数为4;若将点A,C分为第I类,点B,D,E分为第Ⅱ类:分类系数为5;若将点A,D分为第I类,点B,C,E分为第Ⅱ类:d1=d(A,D)=|xA﹣xD|=3,d2=d(B,E)=|yB﹣yE|=5,因为d2>d1,所以分类系数为5;若将点A,E分为第I类,点B,C,D分为第Ⅱ类:d1=d(A,E)=|xA﹣xE|=4,d2=d(B,C)=|yB﹣yC|=4,因为d1=d2,所以分类系数为4;若将点B,C分为第I类,点A,D,E分为第Ⅱ类:d1=d(B,C)=|yB﹣yC|=4,d2=d(A,E)=|xA﹣xE|=4,因为d1=d2,所以分类系数为4;若将点B,D分为第I类,点A,C,E分为第Ⅱ类:d1=d(B,D)=|xB﹣xD|=2,d2=d(A,E)=|xA﹣xE|=4,因为d2>d1,所以分类系数为4;若将点B,E分为第I类,点A,C,D分为第Ⅱ类:d1=d(B,E)=|yB﹣yE|=5,d2=d(A,D)=|xA﹣xD|=3,因为d1>d2,所以分类系数为5;若将点C,D分为第I类,点A,B,E分为第Ⅱ类:d1=d(C,D)=|yC﹣yD|=2,d2=d(B,E)=|yB﹣yE|=5,因为d2>d1,所以分类系数为5;若将点C,E分为第I类,点A,B,D分为第Ⅱ类:d1=d(C,E)=|xC﹣xE|=2,d2=d(A,B)=|yA﹣yB|=4,因为d2>d1,所以分类系数为4;若将点D,E分为第I类,点A,B,C分为第Ⅱ类:d1=d(D,E)=|yD﹣yE|=3,d2=d(A,B)=|yA﹣yB|=4,因为d2>d1,所以分类系数为4;比较得:分类系数d的最小值为4;(3)当点F在点E的右边时,|xF﹣xA|≤5,m﹣1≤5;当点F在点A的左边时,|xF﹣xE|≤5,5﹣m≤5,得0≤m≤6.故m的取值范围是:0≤m≤6.考点02:两点间的距离公式9.(2022春•忠县期末)当点A(x﹣1,3)到点B(﹣2,2y+5)的距离最短时,点P(x,y)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限解:根据题意得AB==,∵(x+1)2≥0,(2y+2)2≥0,∴当x+1=0,2y+2=0时,AB最小,解得x=﹣1,y=﹣1,∴点P的坐标为(﹣1,﹣1),∴P点在第三象限.故选:C.10.(2022春•河西区期末)在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)解:依题意可得:∵AC∥x轴,A(﹣3,2)∴y=2,根据垂线段最短,当BC⊥AC于点C时,点B到AC的距离最短,即BC的最小值=5﹣2=3,此时点C的坐标为(3,2),故选:D.11.(2023春•海淀区校级期末)A(0,a),B(3,5)是平面直角坐标系中的两点,线段AB长度的最小值为 3 .解:如图.∵A(0,a),∴A在y轴上.∴线段AB的长度为B点到y轴上点的距离.若使得线段AB长度的最小,由垂线段最短,∴当A在(0,5)时,即AB⊥y轴,线段AB长度最小.∴(dAB)min=3.故答案为:3.12.(2019春•新余期末)对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”,例如:P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P′(9,6).若点P在x轴的正半轴上,点P的“k属派生点”为点P′,且线段PP′的长度为线段OP长度的5倍,则k的值为 ±5 .解:设P(m,0)(m>0),由题意:P′(m,mk),∵PP′=5OP,∴|mk|=5m,∵m>0,∴|k|=5,∴k=±5.故答案为:±5.13.(2023秋•射阳县校级期末)阅读下列一段文字,然后回答下列问题:已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:MN=.例如:已知P(3,1)、Q(1,﹣2),则这两点的距离PQ==.特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1﹣x2|或|y1﹣y2|.(1)已知A(1,2)、B(﹣2,﹣3),试求A、B两点间的距离;(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离;(3)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.解:(1)AB==;(2)AB=5﹣(﹣1)=6;(3)△ABC为直角三角形.理由如下:∵AB==,AC==2,BC==5,∴AB2+AC2=BC2,∴△ABC为直角三角形.14.(2023•张家界模拟)问题情境:在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;【应用】:(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 3 .(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 (1,2)或(1,﹣2) .【拓展】:我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.解决下列问题:(1)如图2,已知E(2,0),若F(﹣1,﹣2),则d(E,F) =5 ;(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= 2或﹣2 .(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= 4或8 .解:【应用】:(1)AB的长度为|﹣1﹣2|=3.故答案为:3.(2)由CD∥y轴,可设点D的坐标为(1,m),∵CD=2,∴|0﹣m|=2,解得:m=±2,∴点D的坐标为(1,2)或(1,﹣2).故答案为:(1,2)或(1,﹣2).【拓展】:(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.故答案为:=5.(2)∵E(2,0),H(1,t),d(E,H)=3,∴|2﹣1|+|0﹣t|=3,解得:t=±2.故答案为:2或﹣2.(3)由点Q在x轴上,可设点Q的坐标为(x,0),∵三角形OPQ的面积为3,∴|x|×3=3,解得:x=±2.当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.故答案为:4或8.15.(2023•安徽模拟)先阅读下列一段文字,在回答后面的问题.已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.解:(1)∵A(2,4)、B(﹣3,﹣8),∴|AB|==13,即A、B两点间的距离是13;(2)∵A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,∴|AB|=|﹣1﹣5|=6,即A、B两点间的距离是6;(3)△ABC是等腰三角形,理由如下:∵一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),∴AB=5,BC=6,AC=5,∴AB=AC,∴△ABC是等腰三角形.考点03:关于x轴、y轴对称的点的坐标16.(2023秋•历下区期末)已知有序数对(a,b)及常数k,我们称有序数对(ka+b,a﹣b)为有序数对(a,b)的“k阶结伴数对”.如(3,2)的“1阶结伴数”对为(1×3+2,3﹣2)即(5,1).若有序数对(a,b)(b≠0)与它的“k阶结伴数对”关于y轴对称,则此时k的值为( )A.﹣2 B.﹣ C.0 D.﹣解:有序数对(a,b)(b≠0)它的“k阶结伴数对”为(ka+b,a﹣b),∵(a,b)与(ka+b,a﹣b)关于y轴对称,∴a=﹣ka﹣b,b=a﹣b,解得k=﹣,故选:B.17.(2022春•洛江区期末)点P(﹣5,3)关于x轴对称点P的坐标为( )A.(﹣5,﹣3) B.(5,3) C.(5,﹣3) D.(3,﹣5 )解:点P(﹣5,3)关于x轴对称点P的坐标为(﹣5,﹣3),故选:A.18.(2022•皇姑区二模)若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在第 四 象限.解:由题意,得a﹣2=1,b+5=3,解得a=3,b=﹣2,点C(a,b)在第四象限,故答案为:四.19.(2023秋•温州期末)在平面直角坐标系中,点(﹣1,2)关于y轴对称的点的坐标是 (1,2) .解:由点(﹣1,2)关于y轴对称的点的坐标是(1,2).故答案为:(1,2).20.(2019秋•昌平区校级期末)如图,请作出△PQR关于y轴对称的△P1Q1R1,写出它们的坐标P1 (4,﹣1) ,Q1 (1,4) ,R1 (﹣1,1) 解:如图,△P1Q1R1即为所求.观察图象可知:P1(4,﹣1)、Q1(1,4)、R1(﹣1,1),故答案为(4,﹣1),(1,4),(﹣1,1).21.(2016秋•天桥区期末)如图,已知△ABC的顶点坐标分别为A(﹣2,4),B(﹣6,0),C(﹣1,0).请将点A,B,C的横坐标分别乘以﹣1,纵坐标保持不变,分别得到点A′,B′,C′,并依次连接A′,B′,C′,得△A′B′C′;并求出△A′B′C′的面积.解:如图所示,△A′B′C′即为所求,△A′B′C′的面积为×5×4=10.22.(2018秋•东湖区校级期中)如图,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连OB、OC.(1)判断△AOG的形状,并予以证明;(2)若点B、C关于y轴对称,求证:AO⊥BO.解:(1)△AOG是等腰三角形;证明:∵AC∥y轴,∴∠CAO=∠AOG,∵AO平分∠BAC,∴∠CAO=∠GAO,∴∠GAO=∠AOG,∴AG=GO,∴△AOG是等腰三角形;(2)证明:连接BC交y轴于K,过A作AN⊥y轴于N,∵AC∥y轴,点B、C关于y轴对称,∴AN=CK=BK,在△ANG和△BKG中,,∴△ANG≌△BKG,(AAS)∴AG=BG,∵AG=OG,(1)中已证,∴AG=OG=BG,∴∠BOG=∠OBG,∠OAG=∠AOG,∵∠OAG+∠AOG+∠BOG+∠OBG=180°,∴∠AOG+∠BOG=90°,∴AO⊥BO.23.(2019秋•台山市期中)如图是一个平面直角坐标系,按要求完成下列各小题.(1)写出图中的多边形ABCDEF顶点在坐标轴上的点的坐标;(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.解:(1)点A的坐标为(﹣2,0),点B的坐标为(0,﹣3),点D的坐标为(4,0),点F的坐标为(0,3);(2)点B与点C的纵坐标相等,线段BC平行于x轴;(3)点E关于y轴的对称点的坐标为(﹣3,3),它与点C关于原点对称.考点04:坐标与图形变化-对称24.(2022•邗江区校级一模)如图,点A、B的坐标分别为(0,4)、(6,8),点P为x轴上的动点,若点B关于直线AP的对称点B'恰好落在x轴上,则点P的坐标是( )A. B. C.(2,0) D.(3,0)解:如图,连接AB、AB′,∵A(0,4),B(6,8),∴AB==2,∵点B与B′关于直线AP对称,∴AB′=AB=2,在Rt△AOB′中,B′O===6,∴B′点坐标为(﹣6,0)或(6,0),∵A(0,4),点B(6,8)关于直线AP的对称点B′恰好落在x轴上,∴点B(6,8)关于直线AP的对称点B′(﹣6,0),∴B′点坐标为(6,0)不合题意舍去,设直线BB′方程为y=kx+b将B(6,8),B′(﹣6,0)代入得,解得k=,b=4,∴直线BB′的解析式为:y=x+4,∴直线AP的解析式为:y=﹣x+4,当yAP=0时,﹣x+4=0,解得:x=,∴点P的坐标为:(,0);故选:A.25.(2023秋•武城县期末)明明和乐乐下棋,明明执圆形棋子,乐乐执方形棋子,如图,棋盘中心的方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示,明明将第4枚圆形棋子放入棋盘后,所有的棋子构成轴对称图形,则明明放的位置可能是( )A.(﹣1,2) B.(﹣1,3) C.(0,2) D.(﹣1,1)解:将第4枚圆形放在中心方形棋子的正上方一格处,即(﹣1,1)处,构成以过点(﹣1,0),(0,﹣1)的直线为对称轴的轴对称图形.故选:D.26.(2023秋•丰台区期末)在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点.如图,点A的坐标为(2,4),点B的坐标为(1,1),点C为第一象限内的整点.若不共线的A,B,C三点构成轴对称图形,则点C的坐标可以是 (3.1)(答案不唯一) (写出一个即可),满足题意的点C的个数为 6 .解:由不共线的A,B,C三点构成轴对称图形,则△ABC是等腰三角形,如图,共有符合要求的点C有6个.其中点C坐标为(3,1)(答案不唯一),故答案为:(3,1)(不唯一),6.27.(2023秋•盐田区校级期末)欣欣和佳佳下棋,欣欣持圆形棋子,佳佳持方形棋子.若棋盘正中方形棋子的位置用(2,2)表示,右上角方形棋子的位置用(3,3)表示,要使棋盘上所有棋子组成轴对称图形,则欣欣下一枚圆形棋子的位置是 (2,1) .解:第八枚圆形棋子放在位置,如图所示,坐标为(2,1).故答案为:(2,1).28.(2023•黄石港区校级模拟)如图,点A坐标为(0,4),点B坐标为(4,2).直线BC垂直于y轴于点C.点D在直线BC上,点B关于直线AD的对称点在y轴上,则点D的坐标为 (﹣1,2)或(﹣﹣1,2) .解:∵点A坐标为(0,4),点B坐标为(4,2),∴AB==2,∵由题意点D在∠CAB的角平分线或∠CAB的外角平分线上,作DH⊥AB于H.∵DC⊥AC,DH⊥AB,AD平分∠BAC,∴DC=DH,设DC=DH=m,则有•AC•BC=•AC•DC+•AB•DH,∴2×4=2m+2m,∴m=﹣1,∴D(﹣1,2),当D′在∠CAB的外角平分线上时,同法可得CD′=+1,∴D′(﹣﹣1,2)故答案为:(﹣1,2)或(﹣﹣1,2).29.(2023秋•江阴市期中)在平面直角坐标系xOy中,点A(2+2m,1),点B(2﹣m,4),其中m为实数,点O关于直线AB的对称点为C,则AB的最小值为 3 ,点P(﹣2,0)到点C的最大距离为 5+ .解:∵A(2+2m,1),点B(2﹣m,4),∴点A在直线y=1上,点B在直线y=4上,∴AB的最小值为3,如图,设直线AB的解析式为y=kx+b.则有,解得,∴直线AB的解析式为y=﹣•x+3+,∵x=2时,y=3,∴直线AB经过定点D(2,3),连接PD,CD,OD,∵P(﹣2,0),∵PD==5,OD==,∵O,C关于直线AB对称,∴DC=OD=,∴PC≤PD+CD=5+,∴PC的最大值为5+.故答案为:3,5+.30.(2022•和平区校级开学)如图,已知P(﹣2,4),M(﹣1,1),请根据每一问的要求填空:(1)写出P关于y轴的对称点Q的坐标 (2,4) ,M关于y轴的对称点N的坐标 (1,1) ;(2)写出P关于x=1的对称点R的坐标 (4,4) ,则PR的距离为 6 ;(3)写出M关于x轴的对称点T的坐标 (﹣1,﹣1) ,则NT的距离为 2 .解:(1)如图,点Q,点N即为所求,Q(2,4),N(1,1).故答案为:(2,4),(1,1);(2)如图,点R即为所求,R(4,4),PR=6.故答案为:(4,4),6;(3)如图,点T即为所求.T(﹣1,﹣1),NT==2.故答案为:(﹣1,﹣1),2.31.(2023秋•峡江县期末)如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;(2)写出点A′,B′,C′的坐标.解:(1)如图,(2)点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1).32.(2023秋•建阳区期中)如图,P,M关于直线x=1的对称点为P′,M′.(1)写出P′的坐标 (4,4) ,M′的坐标 (3,1) ;(2)思考,写出P(﹣2,4)关于直线x=﹣1的对称点坐标 (0,4) ;写出N′(5,﹣2)关于直线x=2的对称点坐标 (﹣1,﹣2) ;(3)思考,写出点(a,b)关于直线x=n的对称点坐标 (2n﹣a,b) .解:(1)由题意,P′(4,4),M′(3,1),故答案为:(4,4),(3,1);(2)P(﹣2,4)关于直线x=﹣1的对称点坐标(0,4);N′(5,﹣2)关于直线x=2的对称点坐标(﹣1,﹣2).故答案为:(0,4),(﹣1,﹣2);(3)设对称点坐标为(x,y),则有=n,y=b,x=2n﹣a,∴点(a,b)关于直线x=n的对称点坐标(2n﹣a,b).故答案为:(2n﹣a,b).33.(2019秋•咸丰县期末)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);(2)如图1,当0<a<3时,∵P与P1关于y轴对称,P(﹣a,0),∴P1(a,0),又∵P1与P2关于l:直线x=3对称,设P2(x,0),可得:=3,即x=6﹣a,∴P2(6﹣a,0),则PP2=6﹣a﹣(﹣a)=6﹣a+a=6.
相关资料
更多









