2023年中考数学压轴真题汇编(全国通用)4.5多边形和圆的初步认识(分层练习)(原卷版+解析)

这是一份2023年中考数学压轴真题汇编(全国通用)4.5多边形和圆的初步认识(分层练习)(原卷版+解析)，共16页。试卷主要包含了5 多边形和圆的初步认识，14）．，28     6等内容，欢迎下载使用。

精选练习
基础篇
一、单选题
1．（2022·湖北·武汉二中广雅中学八年级阶段练习）六边形的对角线共有（ ）条．
A．5B．9C．12D．14
2．（2022·河北· 沧州渤海新区京师学校八年级阶段练习）用三个不同的正多边形能够铺满地面的是（ ）
A．正三角形、正方形、正五边形B．正三角形、正方形、正六边形
C．正三角形、正方形、正七边形D．正三角形、正方形、正八边形
3．（2020·山东淄博·期中）下列判断：（1）各边长相等的多边形是正多边形；（2）各角都相等的多边形是正多边形；（3）等边三角形是正多边形：（4）长方形是正多边形．其中正确的有（ ）
A．1个B．2个C．3个D．4个
4．（2022·全国·七年级专题练习）下面几何图形中，不属于平面图形的是( )
A．圆锥B．正方形C．扇形D．五角星
5．（2022·四川乐山·七年级期末）一个正多边形每个内角都等于，若用这种多边形拼接地板，需与下列选项中哪种正多边形组合（ ）
A．正三角形B．正四边形C．正五边形D．正六边形
6．（2022·吉林长春·七年级期末）下列正多边形中和正三角形组合，不能铺满地面的是（ ）
A．正方形B．正八边形C．正十二边形D．正六边形
二、填空题
7．（2022·河北· 沧州渤海新区京师学校八年级阶段练习）从边形的一个顶点出发可引______条对角线，它们将n边形分为______个三角形．
8．（2021·山东·泰安市泰山区大津口中学七年级阶段练习）已知从九边形的一个顶点出发，可引出条对角线，这些对角线可以把这个九边形分成个三角形，则________；十三边形的共有________条对角线．
9．（2022·广东湛江·八年级期中）从多边形的一个顶点出发，连接这个点和其他顶点，把多边形分割成16个三角形，则这个多边形的边数是 _____．
10．（2022·安徽·定远县程桥学校七年级阶段练习）如图，图中阴影部分的面积可以用字母表示为 _____．
三、解答题
11．（2021·吉林·乾安县教师进修学校八年级期中）一个多边形的内角和是它的外角和的4倍，求这个多边形的边数和对角线条数．
12．（2022·湖北·大悟县实验中学七年级阶段练习）求出下图阴影部分的周长和面积．单位：厘米（圆周率用π表示）
提升篇
一、填空题
1．（2022·陕西汉中·七年级期末）用等边三角形和正方形作平面镶嵌，则在它的每个顶点周围有个等边三角形和______ 个正方形．
2．（2022·山东威海·七年级期中）已知：从边形的一个顶点出发共有条对角线；从边形的一个顶点出发的所有对角线把边形分成个三角形；正边形的边长为，周长为．则的值为________．
3．（2021·全国·八年级专题练习）正多边形的一个外角是40°，则这个正多边形从一个顶点出发有__条对角线．
4．（2021·全国·九年级专题练习）一个n边形共有n条对角线，将这个n边形截去一个角后它的边数为__．
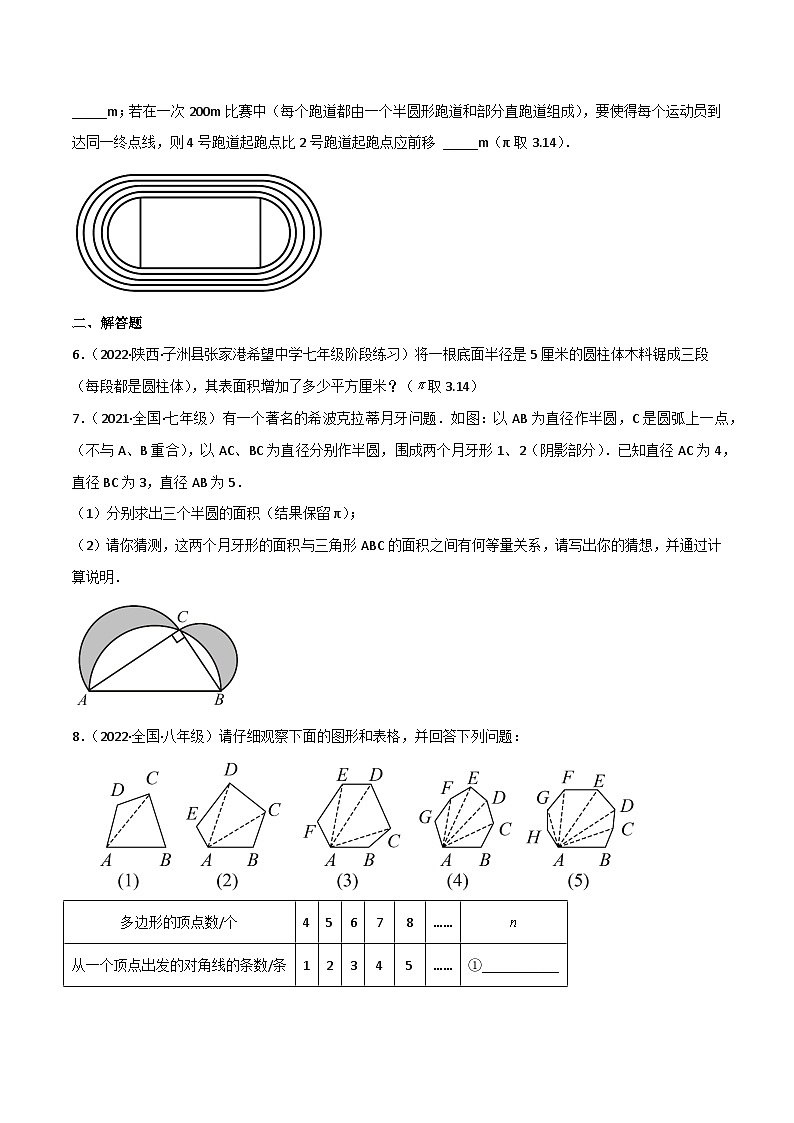
5．（2022·湖北武汉·九年级期末）如图，是编号为1、2、3、4的400m跑道，每条跑道由两条直的跑道和两端是半圆形的跑道组成，每条跑道宽1m，内侧的1号跑道长度为400m，则2号跑道比1号跑道长 _____m；若在一次200m比赛中（每个跑道都由一个半圆形跑道和部分直跑道组成），要使得每个运动员到达同一终点线，则4号跑道起跑点比2号跑道起跑点应前移 _____m（π取3.14）．
二、解答题
6．（2022·陕西·子洲县张家港希望中学七年级阶段练习）将一根底面半径是5厘米的圆柱体木料锯成三段（每段都是圆柱体），其表面积增加了多少平方厘米？（取3.14）
7．（2021·全国·七年级）有一个著名的希波克拉蒂月牙问题．如图：以AB为直径作半圆，C是圆弧上一点，（不与A、B重合），以AC、BC为直径分别作半圆，围成两个月牙形1、2（阴影部分）．已知直径AC为4，直径BC为3，直径AB为5．
（1）分别求出三个半圆的面积（结果保留π）；
（2）请你猜测，这两个月牙形的面积与三角形ABC的面积之间有何等量关系，请写出你的猜想，并通过计算说明．
8．（2022·全国·八年级）请仔细观察下面的图形和表格，并回答下列问题：
（1）观察探究：请自己观察上面的图形和表格，并用含的代数式将上面的表格填写完整，其中①______________________；②______________________；
（2）实际应用：数学社团共分为6个小组，每组有3名同学．同学们约定，大年初一时不同组的两位同学之间要打一个电话拜年，请问，按照此约定，数学社团的同学们一共将拨打电话多少个？
多边形的顶点数/个
4
5
6
7
8
……
从一个顶点出发的对角线的条数/条
1
2
3
4
5
……
①___________
多边形对角线的总条数/条
2
5
9
14
20
……
②___________
第四章 基本平面图形
4.5 多边形和圆的初步认识
精选练习
基础篇
一、单选题
1．（2022·湖北·武汉二中广雅中学八年级阶段练习）六边形的对角线共有（ ）条．
A．5B．9C．12D．14
【答案】B
【分析】根据多边形的对角线有条，即可求解．
【详解】解：六边形的对角线共有条，
故选B．
【点睛】本题考查了多边形对角线条数，掌握多边形的对角线有条是解题的关键．
2．（2022·河北· 沧州渤海新区京师学校八年级阶段练习）用三个不同的正多边形能够铺满地面的是（ ）
A．正三角形、正方形、正五边形B．正三角形、正方形、正六边形
C．正三角形、正方形、正七边形D．正三角形、正方形、正八边形
【答案】B
【分析】先分别求出正三角形、正方形、正五边形、正六边形、正七边形、正八边形的每个内角，然后根据平面镶嵌的条件解答即可．
【详解】解：用公式分别解出正三角形的内角是60°，正方形的内角是90°，正五边形的内角是108°，正六边形内角是120°，正七边形内角是129°，正八边形内角是135°，
A、正三角形、正方形、正五边形内角分别为60°、90°、108°，显然不能构成360°的周角，故不能铺满；
B、正三角形、正方形、正六边形内角分别为60°、90°、120°，当60°+90°+90°+120°=360°，故能铺满；
C、正三角形、正方形、正七边形内角分别为60°、90°、129°，显然不能构成360°的周角，故不能铺满；
D、正三角形、正方形、正八边形内角分别为60°、90°、135°，显然不能构成360°的周角，故不能铺满．
故选：B．
【点睛】本题主要考查了镶嵌的条件，镶嵌的条件是看位于同一顶点处的几个角之和能否为360°．
3．（2020·山东淄博·期中）下列判断：（1）各边长相等的多边形是正多边形；（2）各角都相等的多边形是正多边形；（3）等边三角形是正多边形：（4）长方形是正多边形．其中正确的有（ ）
A．1个B．2个C．3个D．4个
【答案】A
【分析】各个角都相等，各个边都相等的多边形叫做正多边形．依据正多边形的概念进行判断即可．
【详解】解：（1）菱形各边相等，但不是正四边形，故说法错误；
（2）长方形各角都相等，但不是正四边形，故说法错误；
（3）等边三角形三条边都相等，三个角都相等，是正多边形，故说法正确；
（4）长方形的四个角相等，但长与宽不一定相等，所以不一定是正多边形，故说法错误．
故正确的有：1个．
故说：A．
【点睛】本题考查了正多边形的概念，各个角都相等，各个边都相等的多边形叫做正多边形．
4．（2022·全国·七年级专题练习）下面几何图形中，不属于平面图形的是( )
A．圆锥B．正方形C．扇形D．五角星
【答案】A
【分析】根据几何图形的定义逐项分析即可．
【详解】解：A．圆锥各部分不在同一平面上，是立体图形，不是平面图形；
B．正方形 的各部分都在同一平面内，是平面图形；
C．扇形的各部分都在同一平面内，是平面图形；
D．五角星的各部分都在同一平面内，是平面图形；
故选A．
【点睛】本题考查了几何图形的定义，几何图形分为立体图形和平面图形，各部分不在同一平面内的图形叫做立体图形；各部分都在同一平面内的图形叫做平面图形．点、直线、线段、射线、三角形、四边形等为平面图形；长方体、圆球、圆锥等为立体图形．
5．（2022·四川乐山·七年级期末）一个正多边形每个内角都等于，若用这种多边形拼接地板，需与下列选项中哪种正多边形组合（ ）
A．正三角形B．正四边形C．正五边形D．正六边形
【答案】A
【分析】正多边形镶嵌有三个条件限制：①边长相等；②顶点公共；③在一个顶点处各正多边形的内角之和为360°，根据镶嵌的条件解答即可．
【详解】解：一个正多边形每个内角都等于，
，
需要正三角形，
故选：．
【点睛】此题考查平面图形镶嵌，关键是根据在一个顶点处各正多边形的内角之和为360°解答．
6．（2022·吉林长春·七年级期末）下列正多边形中和正三角形组合，不能铺满地面的是（ ）
A．正方形B．正八边形C．正十二边形D．正六边形
【答案】B
【分析】根据判断一种或几种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能判断即可．
【详解】解：A选项，正方形的每个内角等于90°，90°×2+60°×3=360°，故该选项不符合题意；
B选项，正八边形的每个内角等于135°，与正三角形不能铺满地面，故该选项符合题意；
C选项，正十二边形的每个内角等于150°，150°×2+60°=360°，故该选项不符合题意；
D选项，正六边形的每个内角等于120°，120°×2+60°×2=360°，故该选项不符合题意；
故选：B．
【点睛】本题考查了平面镶嵌（密铺），掌握“判断一种或几种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能”是解题的关键．
二、填空题
7．（2022·河北· 沧州渤海新区京师学校八年级阶段练习）从边形的一个顶点出发可引______条对角线，它们将n边形分为______个三角形．
【答案】 ##（2+n） ##（3+n）
【分析】根据多边形的对角线的条数，以及对角线分割三角形的个数的计算公式进行计算即可．
【详解】解：从边形的一个顶点出发有：条对角线，把边形分割成：个三角形；
∴边形的一个顶点出发可引：条对角线，把边形分割成：个三角形；
故答案为：；．
【点睛】本题考查多边形的对角线的条数以及多边形的对角线分割三角形的个数．熟练掌握相关公式是解题的关键．
8．（2021·山东·泰安市泰山区大津口中学七年级阶段练习）已知从九边形的一个顶点出发，可引出条对角线，这些对角线可以把这个九边形分成个三角形，则________；十三边形的共有________条对角线．
【答案】 -1 65
【分析】根据边数为a条边的多边形的任意一点连其他各点得到的对角线条数为（a-3）；组成的三角形的个数为（a-2），分别求出m、n的值即可得出；根据边数为a条边的多边形的对角线条数为，求出十三边形对角线条数即可．
【详解】解：∵边数为a条边的多边形的任意一点连其他各点得到的对角线条数为（a-3）；组成的三角形的个数为（a-2），
∴从九边形的一个顶点出发，对角线共有条，分成个三角形，
即，，
∴；
十三边形的对角线共有：（条）．
故答案为：-1；65．
【点睛】本题主要考查了多边形的对角线问题，熟记n边形的任意一点连其他各点得到的对角线条数为（n-3）及组成的三角形的个数为（n-2），是解题的关键．
9．（2022·广东湛江·八年级期中）从多边形的一个顶点出发，连接这个点和其他顶点，把多边形分割成16个三角形，则这个多边形的边数是 _____．
【答案】18
【分析】从一个n边形的某个顶点出发，可以引（n-3）条对角线，把n边形分为（n-2）个三角形．
【详解】解：由题意可知，n-2=16，
解得n=18．
则这个多边形的边数为18．
故答案为：18．
【点睛】此题主要考查了多边形，关键是掌握从一个n边形的某个顶点出发，可以把n边形分为（n-2）个三角形．
10．（2022·安徽·定远县程桥学校七年级阶段练习）如图，图中阴影部分的面积可以用字母表示为 _____．
【答案】
【分析】先计算出圆的面积，再计算出三角形的面积，阴影部分的面积等于圆的面积减去三角形的面积．
【详解】解：圆的面积为，
由题意得三角形为等腰直角三角形，
∴三角形的面积为，
∴阴影部分的面积为，
故答案为：．
【点睛】本题考查圆和等腰直角三角形的性质，解题的关键是掌握圆和等腰直角三角形的相关知识．
三、解答题
11．（2021·吉林·乾安县教师进修学校八年级期中）一个多边形的内角和是它的外角和的4倍，求这个多边形的边数和对角线条数．
【答案】10，35
【详解】解：设这个多边形的边数是n，则（n-2）×180°=360°×4．n-2=8，n=10．
对角线共有×10×（10-3）=35条，
答：这个多边形的边数是10，对角线条数为35．
【点睛】本题主要考查多边形内角与外角的知识点，此题比较简单，只要结合多边形的内角和公式寻求等量关系，构建方程求解即可．从n边形一个顶点可以引n−3条对角线．
12．（2022·湖北·大悟县实验中学七年级阶段练习）求出下图阴影部分的周长和面积．单位：厘米（圆周率用π表示）
【答案】阴影部分的周长为（6π+16）厘米，面积为（48-9π）平方厘米
【分析】根据阴影部分的周长＝一个圆的周长+矩形长的2倍，阴影部分的面积＝矩形的面积﹣一个圆面积计算即可．
【详解】解：由题意知，周长＝π×6+2×8＝6π+16（厘米）；
面积＝8×6﹣π×＝48﹣9π（平方厘米），
答：阴影部分的周长为（6π+16）厘米，面积为（48-9π）平方厘米．
【点睛】本题主要考查圆的周长和面积公式，熟练掌握圆的周长和面积公式是解题的关键．
提升篇
一、填空题
1．（2022·陕西汉中·七年级期末）用等边三角形和正方形作平面镶嵌，则在它的每个顶点周围有个等边三角形和______ 个正方形．
【答案】
【分析】根据正多边形的组合能镶嵌成平面的条件可知，位于同一顶点处的几个角之和为如果设用个正三角形，个正四边形，则有，求出此方程的正整数解即可．
【详解】解：设用个正三角形，个正四边形能进行平面镶嵌．
由题意，有，
解得，
当时，．
故在它的每个顶点周围，有个正三角形和个正方形．
故答案为：．
【点睛】本题考查了平面镶嵌密铺几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．
2．（2022·山东威海·七年级期中）已知：从边形的一个顶点出发共有条对角线；从边形的一个顶点出发的所有对角线把边形分成个三角形；正边形的边长为，周长为．则的值为________．
【答案】-1
【分析】根据题意，由多边形的周长及性质“从n边形的一个顶点出发，能引出(n﹣3)条对角线，一共有条对角线，经过多边形的一个顶点的所有对角线把多边形分成(n﹣2)个三角形”，分析出m、n、t的值并代入计算即可得到答案．
【详解】解：由题意可知，，，，
∴．
故答案为：-1．
【点睛】本题主要考查了多边形的性质，理解并掌握多边形的相关性质是解题关键．
3．（2021·全国·八年级专题练习）正多边形的一个外角是40°，则这个正多边形从一个顶点出发有__条对角线．
【答案】6
【分析】利用多边形的外角和是360°，正多边形的每个外角都是40°，即可求出这个正多边形的边数，再根据n边形从一个顶点出发可引出（n﹣3）条对角线可求答案．
【详解】解： 360°÷40°＝9，
9﹣3＝6．
故这个正多边形从一个顶点出发可以作的对角线条数是6．
故答案为：6．
【点睛】本题考查的是正多边形的外角和定理，多边形的对角线，掌握利用多边形的外角和求解多边形的边数是解题的关键．
4．（2021·全国·九年级专题练习）一个n边形共有n条对角线，将这个n边形截去一个角后它的边数为__．
【答案】6、5、4
【分析】根据一个n边形对角线条数公式共有n条对角线，列等式，求出边数，再利用分类将五边形截去一个角的情形求解即可．
【详解】解：由这个n边形共有n条对角线，可得，
解得n＝5或0（不合题意，舍去），
所以这个多边形是五边形，
将一个五边形截去一个角，根据截法不同可以有三种情况如图，
其结果分别是6、5、4条边，
故答案为：6、5、4．
【点睛】本题考查由对角线条数与边关，分类思想，数形结合思想截取一个角实质看边是否减少是解题关键．
5．（2022·湖北武汉·九年级期末）如图，是编号为1、2、3、4的400m跑道，每条跑道由两条直的跑道和两端是半圆形的跑道组成，每条跑道宽1m，内侧的1号跑道长度为400m，则2号跑道比1号跑道长 _____m；若在一次200m比赛中（每个跑道都由一个半圆形跑道和部分直跑道组成），要使得每个运动员到达同一终点线，则4号跑道起跑点比2号跑道起跑点应前移 _____m（π取3.14）．
【答案】 6.28 6.28
【分析】利用各跑道直线跑道相等，每条跑道宽1m，两个半圆相加得一个整圆列出式子对比即可．
【详解】解：设直线部分长为l米
1号：
2号：
3号：
4号：
2号比1号长：
4号起点比2号起点前移：
故答案为：6.28，6.28
【点睛】本题考查了列代数式，圆的周长公式，整式的加减等知识点，熟练掌握是解题的关键．
二、解答题
6．（2022·陕西·子洲县张家港希望中学七年级阶段练习）将一根底面半径是5厘米的圆柱体木料锯成三段（每段都是圆柱体），其表面积增加了多少平方厘米？（取3.14）
【答案】314平方厘米
【分析】将圆柱体木料锯成三段表面积增加了4个圆柱的底面圆面积，据此列式计算即可．
【详解】解：圆柱截成三段后，表面积增加了4个圆柱的底面圆面积．
所以（平方厘米）．
答：表面积增加了314平方匣米．
【点睛】本题主要考查了圆的面积，明确将圆柱体木料锯成三段表面积增加了4个圆柱的底面圆面积是解答本题的关键．
7．（2021·全国·七年级）有一个著名的希波克拉蒂月牙问题．如图：以AB为直径作半圆，C是圆弧上一点，（不与A、B重合），以AC、BC为直径分别作半圆，围成两个月牙形1、2（阴影部分）．已知直径AC为4，直径BC为3，直径AB为5．
（1）分别求出三个半圆的面积（结果保留π）；
（2）请你猜测，这两个月牙形的面积与三角形ABC的面积之间有何等量关系，请写出你的猜想，并通过计算说明．
【答案】（1）π，2π，π；（2）两个月牙形的面积之和等于三角形ABC的面积，理由见解析
【分析】（1）由圆的直径可得圆的半径，根据圆的面积公式求解即可；
（2）可设四个月牙的面积依次为S1，S2，S3，S4，则半圆的面积可用月牙形的面积之和表示出来，由（1）又可得SAB为直径＝SAC为直径＋SBC为直径＝π，将半圆的面积代入整理可得结论；
【详解】解：（1）以AB为直径的半圆：
SAB为直径＝π×（）2＝π，
以AC为直径的半圆：
SAC为直径＝π×22＝2π，
以BC为直径的半圆：
SBC为直径＝π×（）2＝π，
（2）两个月牙形的面积之和等于三角形ABC的面积．
设四个月牙的面积依次为S1，S2，S3，S4，如图，
于是，S1＋S2＝SBC为直径＝π，S3＋S4＝SBC为直径＝2π，
∴S1＋S2＋S3＋S4＝SBC为直径＋SBC为直径
SAB为直径＝S2＋S4＋S△ABC，
又由（1）可得：∴SAB为直径＝SAC为直径＋SBC为直径＝π，
S1＋S2＋S3＋S4＝S2＋S4＋S△ABC
∴S1＋S3＝S△ABC，
即：两个月牙形的面积之和等于三角形ABC的面积．
【点睛】本题主要考查圆的面积计算公式，熟练运用数形结合的思想进行图形面积之间的转化是解题的关键．
8．（2022·全国·八年级）请仔细观察下面的图形和表格，并回答下列问题：
（1）观察探究：请自己观察上面的图形和表格，并用含的代数式将上面的表格填写完整，其中①______________________；②______________________；
（2）实际应用：数学社团共分为6个小组，每组有3名同学．同学们约定，大年初一时不同组的两位同学之间要打一个电话拜年，请问，按照此约定，数学社团的同学们一共将拨打电话多少个？
【答案】（1）①；②；（2）135个
【分析】（1）观察表可知从一个顶点出发的对角线的条数是多边形的顶点数减3，即得n-3，由此可完成①；从一个顶点可以引出n－3条对角线，则n个顶点可以引出n(n-3)条，其中每一条都重复算了一次，则可完成②；
（2）把6个组共18名学生看成18边形的顶点，不同组的两位同学之间打一个电话是这个多边形的对角线，因此问题转化为有多少条对角线的问题，由（1）中结论即可完成。
【详解】（1）由表可得，当多边形的顶点数为n时，从一个顶点出发的对角线的条数为n-3；从一个顶点可以引出n－3条对角线，则n个顶点可以引出n(n-3)条，其中每一条都重复算了一次，因此实际的对角线条数为．
故答案为：①；②
（2）因为（名），18名学生看成是顶点数为18的多边形，不同组的两位同学之间打一个电话是这个多边形的对角线，则由（1）可得，数学社团的同学们一共将拨打电话为（个）．
【点睛】本题考查了多边形对角线规律及其应用，难点是理解这个规律的应用：同组三个人之间不能打电话，对应多边形的一个顶点不能与相邻的两个顶点连成对角线，因此18个人对应18个顶点，不同组的两位同学间打一个电话对应连接两顶点的一条对角线.
多边形的顶点数/个
4
5
6
7
8
……
从一个顶点出发的对角线的条数/条
1
2
3
4
5
……
①___________
多边形对角线的总条数/条
2
5
9
14
20
……
②___________