6.3一次函数的图象（1）课件PPT

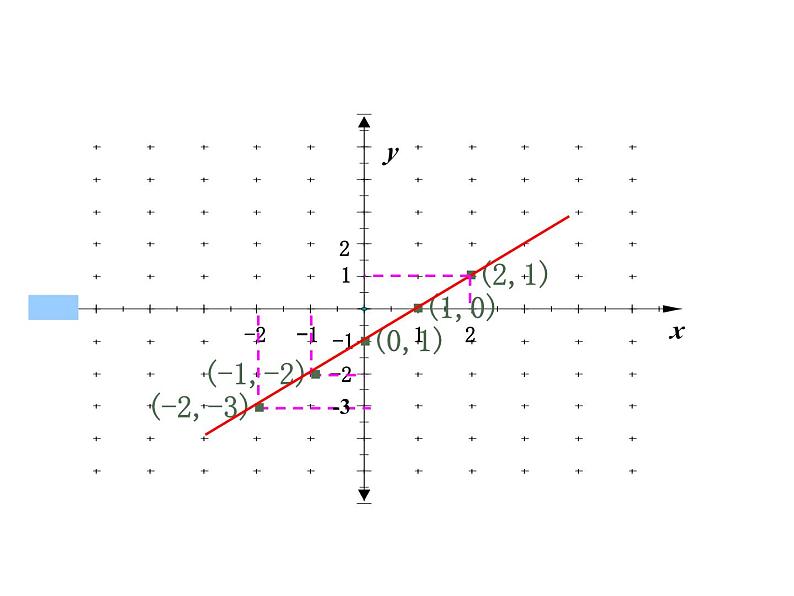
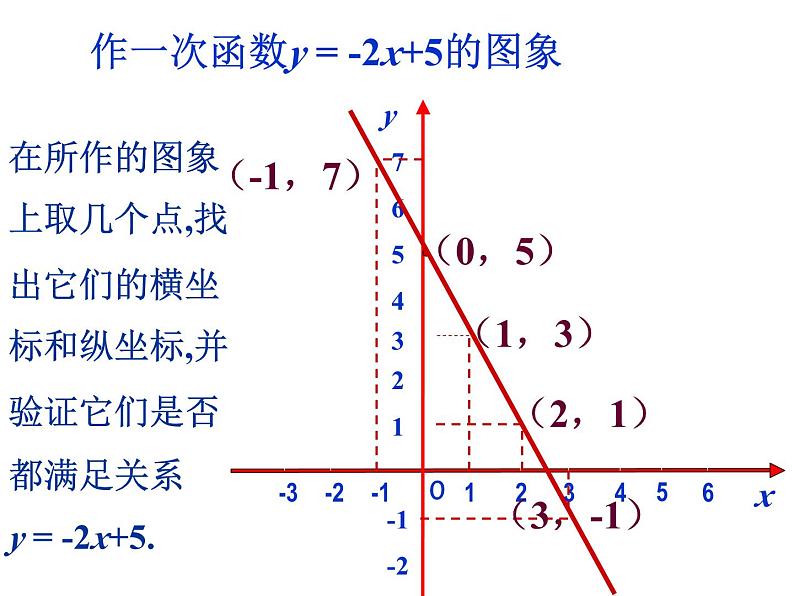
6.3 一次函数的图象(1) 在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.1.什么叫函数?复习回顾2.若两个变量x ,y间的关系式可以表示成_________(k,b为_____且k _____)形式,则称y是x的一次函数(x为_______,y为_______)特别地,当b=___时,称y是x的正比例函数.y=kx+b常数自变量因变量0(1)(2)(5)(6)(2)2．下列函数中，一次函数有 ，正比例函数有 .3．对于一次函数当x=0时，y=_____;当x=1时，y=_____；当x=2时，y=_____;当x=-1时，y=_____；当x=-2时，y=_____.（0，-1）（1，0 ）（2， 1 ）（-1，-2）-101-2-3大家一起来（-2，-3）12-1-2-1-221▪(0,1)▪(1,0)▪(2,1)(-1,-2)▪(-2,-3)▪-3xy把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象.函数图象概念:y0x3（-1，7）（0，5）（1，3）（2，1）（3，-1）作一次函数y = -2x+5的图象在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否都满足关系y = -2x+5. 2． 在所作的图象上取几个点，找出它们的横坐标和纵坐标，并验证它们是否满足关系y= -2x+5 ？1．满足关系式y= -2x+5的x，y所对应的点（x，y）都在一次函数的图象上吗？图象上所有的点都满足关系式.满足关系式的x，y所对应的点（x，y）都在图象上.探究一次函数的图象 所有的一次函数的图象都是一条直线. 由此结论可知做一次函数图象的另一方法：两点法一次函数y=kx+b图象，习惯上也称为直线y=kx+b作出下列一次函数的图象（1）（2）（3）1．已知直线y= (k+1)x＋1-2k，若直线与y轴交于（0，-1），则k=_____；若直线与x轴交于点（3，0），则k=_____.1-42．直线y=-3x+4与x轴的交点坐标是 ________， 与y轴的交点坐标是________.3．下列各点，不在一次函数y＝2x＋1图象上的是　　　　　　　　　　　　　　　　　（　　）A（1，3）B（－1，－1）C（0.5，2）D（0，2）　(0,4)D练一练作出下列两组一次函数的图象，根据所得的图象信息，能得出什么结论？第一组1．y＝2x2．y＝2x＋33．y＝2x－14．y＝3x＋25．y＝0.5x -1第二组1． y ＝－x＋12． y ＝－2x＋43． y ＝－2x－24． y ＝－0.5x－2试一试一次函数y=kx+b有下列性质⑴当k＞0时，y随x的增大而增大⑵当k＜0时，y随x的增大而减小注意：k值相同的一次函数，在图象上反映为它们的图象平行大家一起来归纳一下这节课所学的知识:⑴ 函数图象的概念⑵ 如何作一次函数图象,并能验证某些数据是否在函数图象⑶ 明确一次函数图象是一条直线因此在 作一次函数图象时, 不需要列表,只要确两点就可以了