6.5一次函数的应用（1）课件PPT

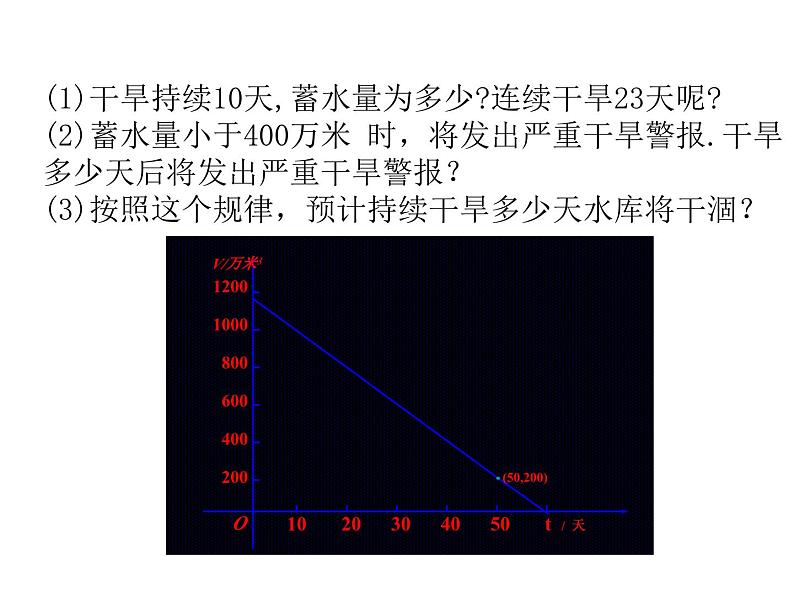
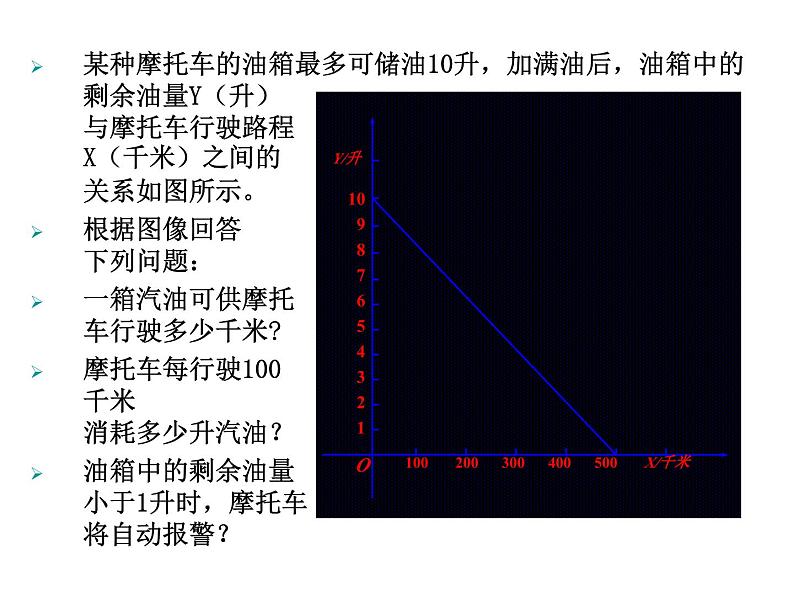
6.5 一次函数的应用(1)1、有哪些方法可以反映两个变量之间的关系？2、已知两点的坐标如何确定一次函数的表达式3、已知一次函数的表达式，如何画出它的图象忆一忆由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少.干旱持续时间T(天)与蓄水量V（万米 ）的关系如图所示，回答下列问题： 10 20 30 40 50 t / 天O(1)干旱持续10天,蓄水量为多少?连续干旱23天呢?(2)蓄水量小于400万米 时，将发出严重干旱警报.干旱多少天后将发出严重干旱警报？(3)按照这个规律，预计持续干旱多少天水库将干涸？某种摩托车的油箱最多可储油10升，加满油后，油箱中的剩余油量Y（升）与摩托车行驶路程X（千米）之间的关系如图所示。根据图像回答下列问题：一箱汽油可供摩托车行驶多少千米?摩托车每行驶100千米消耗多少升汽油？油箱中的剩余油量小于1升时，摩托车将自动报警？100 200 300 400 500 X/千米O解法1：观察图像，得当Y=0时，X=500.一次一箱汽油可供摩托车行驶500千米.X从0增加到100时，Y从10减少到8，减少了2，因此摩托车每行驶100千米消耗2升汽油.当Y=1时，X=450，因此行驶了450千米后，摩托车将自动报警.100 200 300 400 500 X/千米O你会这样做吗？解法：设y=kx+b,把（0,10）（500,0）代入上式 (1) 将y=0代入上式 解得 x=500(2) 将x=100代入上式 解得 y=8 10-8＝2(3)将y=1代入上式 解得 x=450x=____-220131、看图填空：123-1-2-3-1-2-3（1）当y=0时，（2）当x=0时，y=____xy练一练19练一练631215182124y/cml2468101214t/天某植物t天后的高度为ycm,图中的l 反映了y与t之间的关系，根据图象回答下列问题：(1)植物刚栽的时候多高？2）3天后该植物高度为多少？3）几天后该植物高度可达21cm?（4）先写出y与t的关系式，再计算长到100cm需几天？ 一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系？ 从上面的例题和练习不难得出下面的答案：1、从“数”的方面看，当一次函数y=0.5x+1的因变量的值为0时，相应的自变量的值即为方程0.5x+1=0的解.2、从“形”的方面看，函数y=0.5x+1与x轴交点的横坐标，即为方程0.5x+1=0的解.2013123-1-2-3-1-2-3xy议一议2、本节课主要运用什么方法来解决一些简单的实际问题？1、经过本节课的学习，你有哪些收获？小 结