3.1 探索勾股定理（1）课件PPT

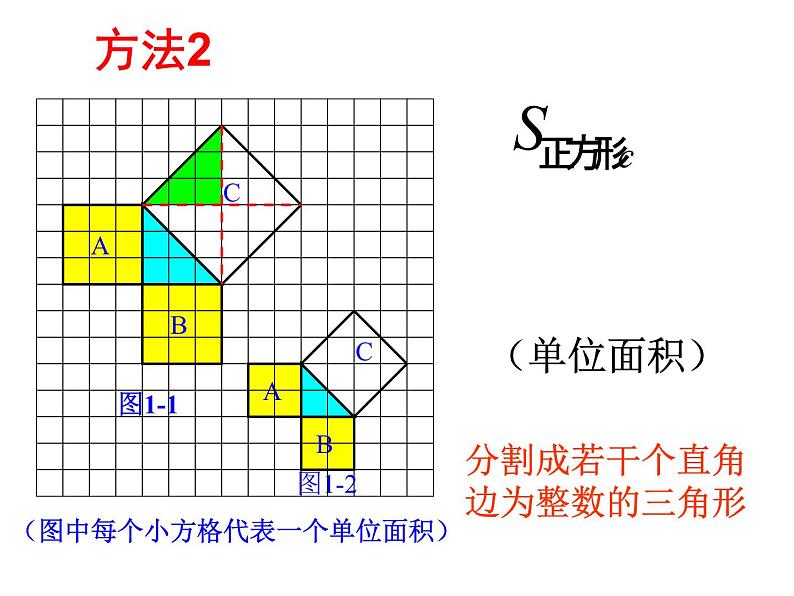
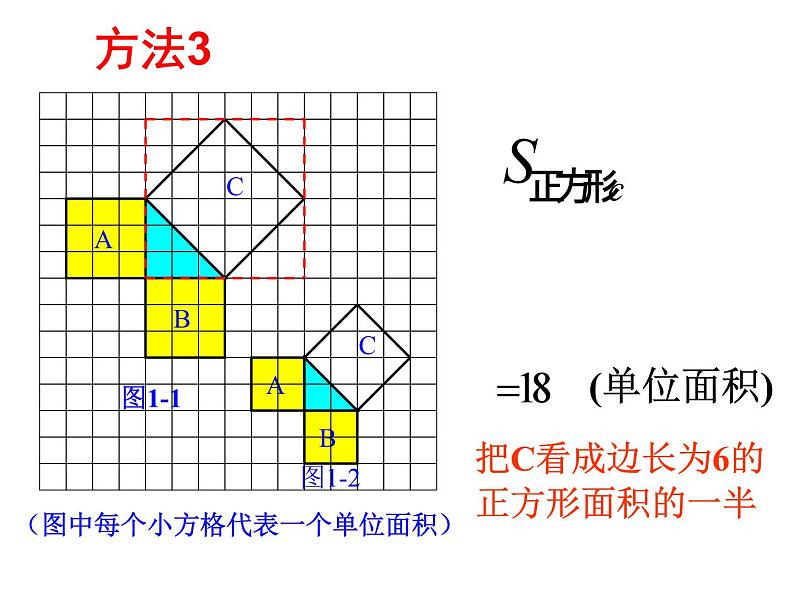
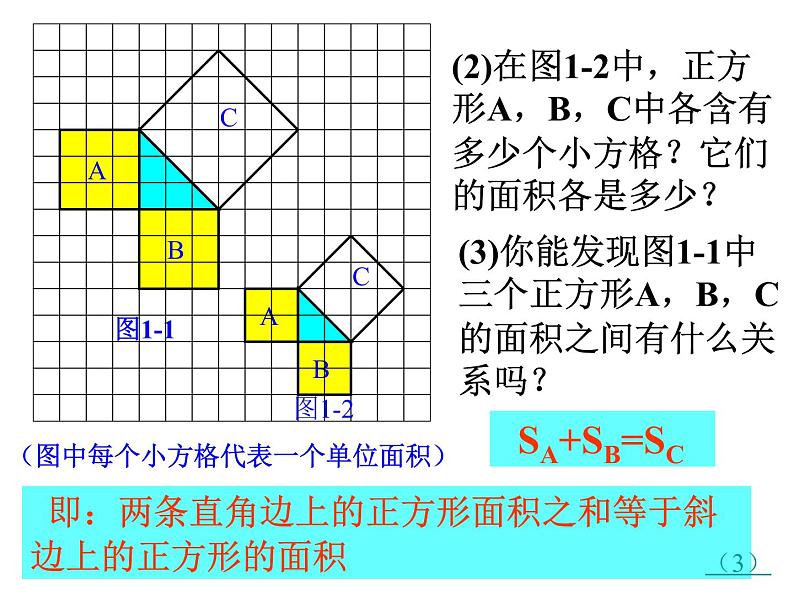
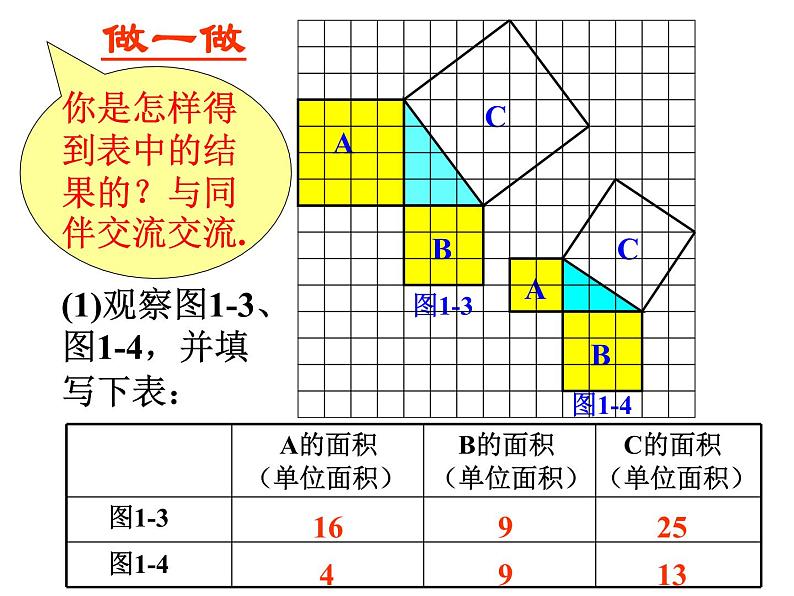
3.1 探索勾股定理（1）思考 如图，从电线杆离地面8 m处向地面拉一条钢索，若这条钢索在地面的固定点距离电线杆底部6 m，那么需要多长的钢索？ 想一想，你需要求哪些线段长度，这些长度能确定吗？(1)观察图1-1 正方形A中含有 . 个小方格，即A的面积是 个单位面积. 正方形B的面积是 个单位面积.正方形C的面积是 个单位面积.99918你是怎样得到上面的结果的？与同伴交流.（2）做一做正方形周边上的格点数a=12正方形内部的格点数b=13图1-1图1-2方法1分割成若干个直角边为整数的三角形（单位面积）方法2(单位面积)把C看成边长为6的正方形面积的一半方法3(2)在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？(3)你能发现图1-1中三个正方形A，B，C的面积之间有什么关系吗？ SA+SB=SC 即：两条直角边上的正方形面积之和等于斜边上的正方形的面积（3）(1)观察图1-3、图1-4，并填写下表： A的面积（单位面积） B的面积（单位面积） C的面积（单位面积）图1-3图1-4169254913做一做分割成若干个直角边为整数的三角形(面积单位)(2)三个正方形A，B，C的面积之间有什么关系？SA+SB=SC即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积(1)你能用三角形的边长表示正方形的面积吗？(2)你能发现直角三角形三边长度之间存在什么关系吗？与同伴进行交流.(3)分别以5厘米、12厘米为直角边作出一个直角三角形，并测量斜边的长度.(2)中的规律对这个三角形仍然成立吗？议一议勾股定理（gou-gu theorem) 如果直角三角形两直角边分别为a、b,斜边为c，那么即 直角三角形两直角边的平方和等于斜边的平方.勾股弦结论 小明的妈妈买了一部29英寸(74厘米)的电视机. 小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了. 你能解释这是为什么吗？∴售货员没搞错∵荧屏对角线大约为74厘米做一做说说这节课你有什么收获？ 内容总结：探索直角三角形两直角边的平方和等于斜边的平方；利用勾股定理解决实际问题.方法总结：① 数方格看图找关系，利用面积不变的方法；② 用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形，再验证自己的发现.小结延伸拓展1、情境引入中的“围地”问题.2、如图，一艘船在A处要到达小岛B处，但AB之间有暗礁，为了行船安全，船先向正西方向行驶了400海里，再向正南方向行驶了300海里便到达了小岛B，请你计算A与B之间的直线距离是多少.3、高速公路上有A、B两站相距25 km，C、D为两个小集镇，DA⊥AB与A，CB⊥AB与B,已知DA＝15 km，CB＝10 km，现在要在公路AB边上建设一个土特产收购站E，使得C、D两镇到E站的距离相等，则E站应建在距A站多少千米处？D一、课后习题二、准备4张全等的直角三角形纸片作业怎样寻找勾股数：1、牢记几组常用的勾股数2、利用公式来推导x=m2-n2 y=2mn z=m2+n2(m、n是任意两个正整数，且m＞n)