专题02：复数-2024年新高考数学新题型试卷结构冲刺讲义

这是一份专题02：复数-2024年新高考数学新题型试卷结构冲刺讲义，文件包含专题二复数解析版docx、专题二复数docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
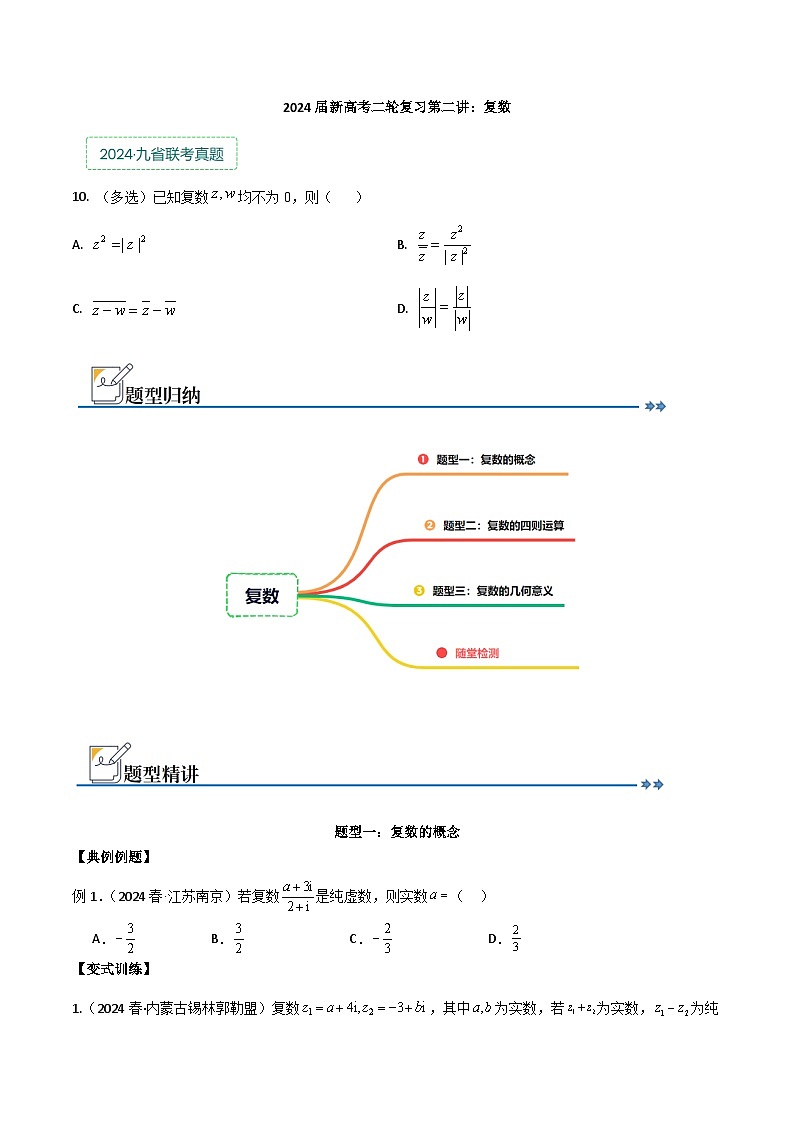
10. 已知复数均不为0，则（ ）
A. B.
C. D.
【答案】BCD
【解析】
【详解】设、；
对A：设，则，
，故A错误；
对B： ，又，即有，故B正确；
对C：，则，
，，则，
即有，故C正确；
对D：
，
，
故，故D正确.
故选：BCD.
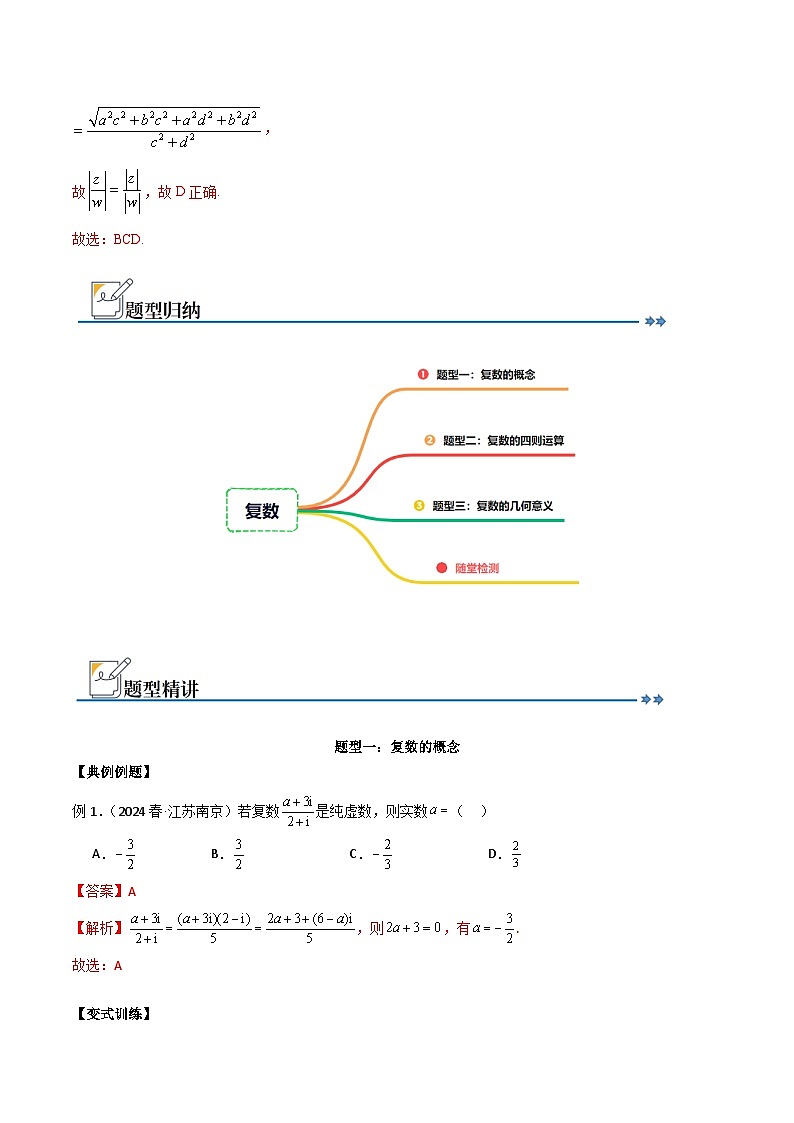
题型一：复数的概念
【典例例题】
例1．（2024春·江苏南京）若复数是纯虚数，则实数（ ）
A．B．C．D．
【答案】A
【解析】，则，有.
故选：A
【变式训练】
1.（2024春·内蒙古锡林郭勒盟）复数，其中为实数，若为实数，为纯虚数，则（ ）
A．6B．C．D．7
【答案】C
【详解】复数，为实数，则，
由为实数，得，解得，又，
显然，由为纯虚数，得，解得，
所以.
故选：C
2．（2024上·河南焦作）已知复数满足，则的虚部为（ ）
A．5B．C．D．
【答案】B
【详解】由题意可得：，
所以的虚部为．
故选：B.
3.（2024春·江苏南通）已知，是方程的两个复根，则（ ▲ ）.
A. 2B. 4C. 2iD. 4i
【答案】B
4.（2024春·上海·高三开学考试）下列命题不正确的为（ ）
A．若复数，的模相等，则，是共轭复数
B．，都是复数，若是虚数，则不是的共轭复数
C．复数是实数的充要条件是
D．，，则对应的点的轨迹为线段
【答案】A
【详解】对于A，若复数，的模相等，则，还可能是相等的复数，故A错误；
对于B，若和是共轭复数，则相加为实数，不会为虚数，故B正确；
对于C，若复数是实数，则，从而，所以，
反之若，则由得，所以，
所以复数是实数的充要条件是，故C正确；
对于D，设，
由复数的几何意义可知表示点到点和距离之和为2，
而点和之间距离为2，所以对应的点的轨迹为线段，故D正确.
故选：A
题型二：复数的四则运算
【典例例题】
例1.（2024春·新高考）（多选）已知复数，满足，，则（ ）
A．B．
C．D．
【答案】ABD
【详解】，，
，，
所以，，
故选:ABD
【变式训练】
1.（2024春·江苏南通）（多选）已知复数，设，当x取大于0的一组实数、、、、时、所得的y值依次为另一组实数、、、、，则（ ▲ ）.
A. 两组数据的中位数相同B. 两组数据的极差相同
C. 两组数据的方差相同D. 两组数据的均值相同
【答案】BC
2.（2024春·广东省）设复数z满足，则（ ）
A．B．C．2D．8
【答案】B
【解析】，
，
因此．
故选：B
3．（2024春·云南保山）（多选）已知，则下列正确的是（ ）
A．B．在复平面内所对应的点在第二象限
C．D．
【答案】AC
【详解】对于A，由，所以，故A正确；
对于B，由，所以，故在复平面内所对应的点为，
在第三象限，故B错误；
对于C，，所以，
则，故C正确；
对于D，，所以，故，故D错误，
故选：AC.
4.（2024·全国·模拟预测）（多选）已知是两个虚数，则下列结论中正确的是（ ）
A．若，则与均为实数B．若与均为实数，则
C．若均为纯虚数，则为实数D．若为实数，则均为纯虚数
【答案】ABC
【详解】设，．，．
若，则，，所以，，所以A正确；
若与均为实数，则，且，又，，所以，所以B正确；
若，均为纯虚数，则，所以，所以C正确；
取，，则为实数，但，不是纯虚数，所以D错误．
故选：ABC．
题型三：复数的几何意义
【典例例题】
例1.（2024春·湖北省）（多选）设为复数，则下列命题中正确的是（ ）
A. B. 若，则复平面内对应的点位于第二象限
C. D. 若，则的最大值为2
【答案】ABD
【解析】
【详解】对于A，设，故，则，，故成立，故A正确，
对于B，，，显然复平面内对应的点位于第二象限，故B正确，
对于C，易知，，当时，，故C错误，
对于D，若，则，而，易得当时，最大，此时，故D正确.
故选：ABD
【变式训练】
1.（2024春·北京海淀）如图，在复平面内，复数，对应的点分别为，，则复数的虚部为（ ）

A．B．C．D．
【答案】D
【详解】在复平面内，复数，对应的点分别为，，
则，，得，
所以复数的虚部为.
故选：D
2.（2024春·江苏常州）在复平面内，复数对应的向量为，复数对应的向量为，那么向量对应的复数是（ ）
A．1B．C．D．
【答案】A
【详解】由题意得，，，
则对应复数1.
故选：A．
3.（2024春·湖南长沙）（多选）已知复数z1，z2在复平面上对应的点分别为A，B，且O为复平面原点若．z1=32+12i（i为虚数单位），向量OA绕原点逆时针方向旋转90°，且模伸长为原来的2倍后与向量OB重合，则（ ）
A．z2的虚部为32B．点B在第二象限
C．z1+z2=2D．z2z1=2
【答案】BD
【详解】因为z1=32+12i， 所以z1对应的坐标为32,12，z1=1，
OA向量与x轴夹角为θ,tanθ=1232=33,θ=π6,

由题意可知，z2=2,且OB=2csθ+π2,sinθ+π2=−1,3，选项B正确；
z2=−1+3i，z2的虚部为3，选项A错误；
z1+z2=32−1+12+3i，所以z1+z2=32−12+12+32=5，选项C错误；
z2z1=z2z1=2，选项D正确；
故选：BD.
4.（2024春·湖北武汉）已知复数z满足（i为虚数单位），则的最小值为______．
【答案】
【解析】
【解答】
解：设，，
由，
即，
则的轨迹为点，连线的中垂线：，
设，，
则的最小值等价于求的最小值，
点关于的对称点，
所以，
故答案为．
单项选择
1．（2024春·湖南衡阳）在复数范围内，是方程的两个不同的复数根，则的值为（ ）
A．1B．C．2D．或2
【答案】D
【详解】由，
得.
因为，所以或，
当或，；
当或，.
故选：D
2．（2024春·山西朔州）是虚数单位，设复数满足，则的共轭复数对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】C
【详解】因为，得.
则.则其在第三象限.
故选：C
3．（2024春·重庆长寿）设复数，则复数的共轭复数的模为（ ）
A．7B．1C．5D．25
【答案】C
【详解】复数，则，
所以.
故选：C.
4．（2024春·全国·模拟预测）已知复数z满足，则z的实部为（ ）
A．B．C．3D．4
【答案】A
【详解】由题意可得，
所以z的实部为．
故选：A．
5．（2024春·河南·模拟预测）（ ）
A．B．C．3D．5
【答案】B
【详解】因为，
所以.
故选：B.
6．（2024春·河北保定）若虚数是关于的方程的一个根，且，则（ ）
A．6B．4C．2D．1
【答案】C
【详解】依题意，设（且），
代入方程，得，
整理得．
所以，解得，
因为，即，所以．
故选：C．
7．（2024春·河南）复数的实部与虚部之和为（ ）
A．0B．2C．4D．8
【答案】C
【详解】，
所以实部与虚部之和为.
故选：C
8．（2024春·黑龙江哈尔滨）已知为虚数单位，若复数，则（ ）
A．复数实部为1 B．复数虚部为0
C． D．在复平面内对应的点位于第二象限
【答案】B
【详解】由题意得：，
所以复数z的实部为，虚部为0，即A错误，B正确；
，故C错误，在复平面内z对应的点为，故D错误，
故选：B.
多项选择
9.（2024春·广东省）已知是复数的共轭复数，则下列说法正确的是（ ）
A． B．若，则
C． D．若，则的最小值为1
【答案】CD
【详解】对于A，设，则，但，故A错误；
对于B，令，满足，故B错误；
对于C，设，则所以，则，所以，故C正确；
对于D，设，则，
即，表示以为圆心，半径为1的圆，
表示圆上的点到的距离，故的最小值为，故D正确.
故选：CD
10.（2024春·江西省）若复数，则（ ）
A．的共轭复数B．
C．复数的虚部为D．复数在复平面内对应的点在第四象限
【答案】ABD
【详解】，则，故正确；
，故正确；复数的虚部为，故错误；
复数在复平面内对应的点为，在第四象限，故正确.
故选：ABD
11.（2024春·九省联考模拟）（多选）已知复数，，则下列结论正确的有（ ）
A. B. C. D.
【答案】BC
【解析】
【详解】设，，其中.
对于选项A: ，所以与不一定相等，故选项A错误；
对于选项B: 因为，
所以，
因为，
所以,故选项B正确；
对于选项C: 因为,
所有
因为，
所以,故选项C正确；
对于选项D:因为，所以
，而与不一定相等,故选项D错误；
故选：BC.
12.（2024春·重庆）已知复数的共轭复数为，则下列命题正确的是（ ）
A． B．为纯虚数
C． D．
【答案】ACD
【详解】设复数，则，故，A正确；
，当时，为实数，B错误；
，则，C正确；
，
，故，
则，D正确，
故选：ACD
13．（2024春·江西宜春）设为复数，则下列命题中正确的是（ ）
A．B．若，则复平面内对应的点位于第二象限
C．D．若，则的最大值为2
【答案】ABD
【详解】对于A，设，故，则，，故成立，故A正确，
对于B，，，显然复平面内对应的点位于第二象限，故B正确，
对于C，易知，，当时，，故C错误，
对于D，若，则，而，易得当时，最大，此时，故D正确.
故选：ABD