北师大版八年级数学下册《高分突破•培优新方法》专题10巧用旋转进行计算(原卷版+解析)

这是一份北师大版八年级数学下册《高分突破•培优新方法》专题10巧用旋转进行计算(原卷版+解析)，共43页。

将一个图形绕着某一点旋转一个角度的图形变换叫做旋转，由旋转的性质可知旋转前后的图形全等，对应点到旋转中心的连线所组成的夹角等于旋转角。旋转法是在图形具有公共端点的相等的线段特征时，可以把图形的某部分绕相等的线段的公共端点，旋转另一位置的引辅助线的方法，主要用途是把分散的元素通过旋转集中起来，从而为证题创造必要的条件。旋转方法常用于等腰三角形、等边三角形及正方形等图形中。
典例分析
【考点1 利用旋转结合等腰(边)三角形、垂直、平行的性质求角度】
【典例1】（2021九上·番禺期末）如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到的△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′．若∠CC′B′＝20°，则∠B的大小是（ ）
A．70°B．65°C．60°D．55°
【变式1-1】（2021九上·上高月考）如图，将△AOB绕着点O顺时针旋转70°，得到△COD，若∠COD=40°，则∠BOC的度数为（ ）
A．10°B．20°C．30°D．40°
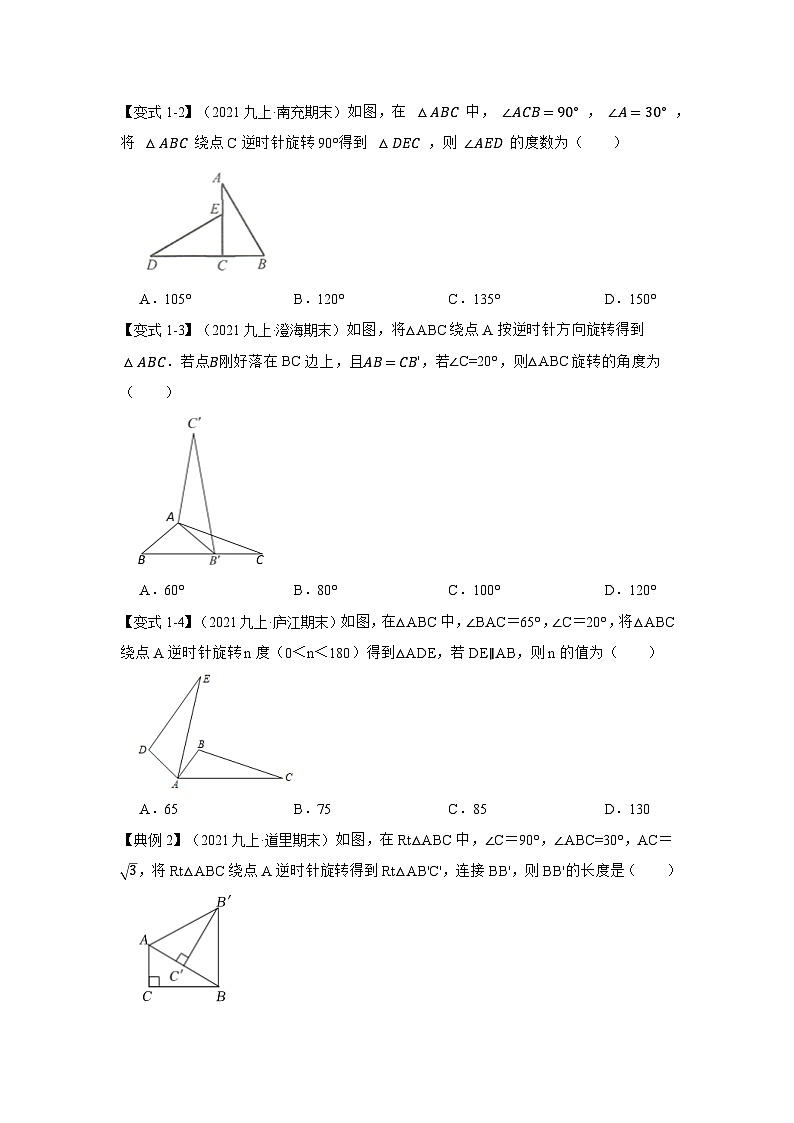
【变式1-2】（2021九上·南充期末）如图，在 △ABC 中， ∠ACB=90° ， ∠A=30° ，将 △ABC 绕点C逆时针旋转90°得到 △DEC ，则 ∠AED 的度数为（ ）
A．105°B．120°C．135°D．150°
【变式1-3】（2021九上·澄海期末）如图，将△ABC绕点A按逆时针方向旋转得到△ABC．若点B刚好落在BC边上，且AB=CB'，若∠C=20°，则△ABC旋转的角度为（ ）
A．60°B．80°C．100°D．120°
【变式1-4】（2021九上·庐江期末）如图，在△ABC中，∠BAC＝65°，∠C＝20°，将△ABC绕点A逆时针旋转n度（0＜n＜180）得到△ADE，若DE∥AB，则n的值为（ ）
A．65B．75C．85D．130
【典例2】（2021九上·道里期末）如图，在Rt△ABC中，∠C＝90°，∠ABC=30°，AC＝3，将Rt△ABC绕点A逆时针旋转得到Rt△AB'C'，连接BB'，则BB'的长度是（ ）
A．1B．3C．3D．23
【变式2-1】（2021九上·香坊期末）如图，将RtΔABC绕点A按顺时针旋转一定角度得到RtΔADE，点B的对应点点D恰好落在边BC上，若AC=23，∠ABC=60°，则CD的长为（ ）
A．3B．2C．3D．1
【变式2-2】（2021秋•韶关期末）如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB＝3cm，则BE等于（ ）
A．2cmB．3cmC．4cmD．5cm
【变式2-3】（2021秋•邓州市期末）如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝1，将△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在AB边上，连结BB'，则△A'BB'的周长为（ ）
A．B．1+C．2+D．3+
【典例3】（2021秋•岳池县期末）如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，连接OD，OA．
（1）求∠ODC的度数；
（2）试判断AD与OD的位置关系，并说明理由；
（3）若OB＝2，OC＝3，求AO的长（直接写出结果）．
【变式3-1】（2021九上·中山期末）如图，在Rt△ABC中，∠C＝90°，将△ABC绕着点B逆时针旋转得到△FBE，点C，A的对应点分别为E，F．点E落在BA上，连接AF．
（1）若∠BAC＝40°，求∠BAF的度数；
（2）若AC＝8，BC＝6，求AF的长．
【变式3-2】（2021九上·谷城期中）如图，P是正三角形ABC内的一点，且PA＝6，PB＝8，PC＝10，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数．
【考点2 利用旋转计算面积】
【典例4】（2021九上·鄞州月考）如图，在△ABC中，AB＝4，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分的面积为 .
【变式4-1】（2022•瑞金市模拟）如图，将边长为的正方形绕点B逆时针旋转30°，那么图中阴影部分的面积为（ ）
A．3B．C．D．
【变式4-2】（2021秋•丰泽区校级期末）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2．将△ABC绕点C按顺时针方向旋转到点D落在AB边上，此时得到△EDC，斜边DE交AC边于点F，则图中阴影部分的面积为（ ）
A．3B．1C．D．
【变式4-3】（2021秋•南丹县期末）如图，边长相等的两个正方形ABCD和OEFG，若将正方形OEFG绕点O按逆时针方向旋转120°，两个正方形的重叠部分四边形OMCN的面积（ ）
A．不变 B．先增大再减小 C．先减小再增大 D．不断增大
【考点3 坐标系中图形旋转的规律】
【典例5】（2021秋•阳东区期末）如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2020次得到正方形OA2020B2020C2020，如果点A的坐标为（1，0），那么点B2020的坐标为（ ）
A．（﹣1，1）B．C．（﹣1，﹣1）D．
【变式5-1】（2021九上·惠来月考）如图，在正方形ABCD中，顶点A，B，C，D在坐标轴上，且B(2，0)，以AB为边构造菱形ABEF．将菱形ABEF与正方形ABCD组成的图形绕点O逆时针旋转，每次旋转45°，则第2020次旋转结束时，点F2020的坐标为（ ）
A．(−2，22) B．(−2，−22) C．(22，−2) D．(−22，−2)
【变式5-2】（2021•张家界）如图，在平面直角坐标系中，将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2019次得到正方形OA2019B2019C2019，那么点A2019的坐标是（ ）
A．（，﹣）B．（1，0）C．（﹣，﹣）D．（0，﹣1）
【变式5-3】（2021秋•郧阳区期末）如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…，若点A（3，0），B（0，4），则点B2021的横坐标为（ ）
A．12120B．12128C．12123D．12125
夯实基础
1．（2021九上·海曙期末）如图， 在 △ABC 中， ∠BAC=75∘ ， 以点 A 为旋转中心， 将 △ABC 绕点 A 逆时针旋转得到 △ADE ， 点 B、C 的对应点分别为 D、E ， 连接 CE ， 若 CE//AB ， 则 ∠CAE 的值是( )
A．25∘B．30∘C．35∘D．45∘
2．（2021九上·虎林期末）如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1cm，将Rt△ABC绕点A逆时针旋转得到Rt△ABC，使点C落在AB边上，连接BB，则BB的长度是（ ）
A．1cmB．2cmC．3cmD．23cm
3．（2022春•泗县期中）如图所示，△ABC为直角三角形，BC为斜边，将△ABP绕点A逆时针旋转后，能与△ACP'重合．如果AP＝3，那么PP'的长等于（ ）
A．B．C．3D．4
4．（2021秋•甘井子区期末）如图，Rt△ABC中，∠ABC＝90°，∠BAC＝60°，AB＝1，将△ABC绕点B顺时针旋转得到△A'BC'，若直线A'C'经过点A，则CC'的长为（ ）
A．1B．2C．D．4
5（2022·呼和浩特）如图，△ABC中，∠ACB=90°，将△ABC绕点C顺时针旋转得到△EDC，使点B的对应点D恰好落在AB边上，AC、ED交于点F．若∠BCD=α，则∠EFC的度数是（用含α的代数式表示）（ ）
A．90°+12αB．90°−12αC．180°−32αD．32α
6．（2021九上·富裕期末）如图，点D是等边△ABC内一点，AD＝3，BD＝3，CD＝32，△ACE是由△ABD绕点A逆时针旋转得到的，则∠ADC的度数是（ ）
A．40°B．45°C．105°D．55°
7．（2022·益阳）如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（ ）
A．①②③ B．①②④ C．①③④D．②③④
8.（2021九上·集贤期末）如图，在△ABC中，∠C＝36°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，且AB′＝CB′，则旋转角为 度．
9．（2022春•通道县期末）已知，正方形ABCD的边长是4，正方形OMNE（OM＞AC）绕着正方形ABCD的对称中心O旋转，那么两正方形重叠部分的面积是 ．
10．（2022•新城区校级一模）如图，D是等边三角形ABC外一点，AD＝6，CD＝4，当BD长最大时，△ABC的面积为 ．
11.（2022春•高州市期末）如图，在△ABC中，AB＝8，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分面积为 ．
12.（2021九上·互助期中）如图将 △ABC 绕点A逆时针旋转得到 △ADE ，点C和点E是对应点，若 ∠CAE=90° ， AB=1 ，求BD的长．
13．如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.
（1）求证：△BDE≌△BCE；
（2）试判断四边形ABED的形状，并说明理由．
14.（涪陵期中）如图，P是正三角形ABC内的一点，且PA=5，PB=12，PC=13，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数．
15．（2022春•渭滨区期末）如图，O是等边△ABC内一点，连接OA、OB、OC，且OA＝3，OB＝4，OC＝5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．
（1）求线段OD的长；
（2）求∠BDC的度数．
16.（2022春•永丰县期中）如图，在△ABC中，BA＝BC，∠ABC＝40°，将△ABC绕点B按逆时针方向旋转110°，得到△DBE，连接AD，CE．
（1）求证：△ABD≌△CBE．
（2）求∠ACE的度数．
能力提升
17．（2021九上·龙江期末）如图，在平面直角坐标系中，四边形ABOC是正方形，点A的坐标为（1，1），AA1⌢是以点B为圆心，BA为半径的圆弧；A1A2⌢是以点O为圆心，OA1为半径的圆弧，A2A3⌢是以点C为圆心，CA2为半径的圆弧，A3A4⌢是以点A为圆心，AA3为半径的圆弧，继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”，那么点A2021的坐标是 ．
18.（2021九上·黔西南期末）如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A1BO1的位置，使点A的对应点A1落在直线y＝33x上，再将△A1BO1绕点A1顺时针旋转到△A1B1Q2的位置，使点O1的对应点O2落在直线y＝33x上，依次进行下去…，若点A的坐标是（0，1），点B的坐标是（3，1），则点A12的横坐标是 .
19．（2021九上·新乡期末）如图，△ABC的顶点A，B分别在x轴，y轴上，∠ABC＝90°，OA＝OB＝1，BC＝22，将△ABC绕点O顺时针旋转，每次旋转90°，则第2021次旋转结束时，点C的坐标为 .
专题解答题技巧
10 巧用旋转进行计算
将一个图形绕着某一点旋转一个角度的图形变换叫做旋转，由旋转的性质可知旋转前后的图形全等，对应点到旋转中心的连线所组成的夹角等于旋转角。旋转法是在图形具有公共端点的相等的线段特征时，可以把图形的某部分绕相等的线段的公共端点，旋转另一位置的引辅助线的方法，主要用途是把分散的元素通过旋转集中起来，从而为证题创造必要的条件。旋转方法常用于等腰三角形、等边三角形及正方形等图形中。
典例分析
【考点1 利用旋转结合等腰(边)三角形、垂直、平行的性质求角度】
【典例1】（2021九上·番禺期末）如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到的△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′．若∠CC′B′＝20°，则∠B的大小是（ ）
A．70°B．65°C．60°D．55°
【答案】B
【解答】解：∵将ΔABC绕点A顺时针旋转90°后得到的△AB'C'，
∴AC=AC，∠CAC=90°，∠B=∠ABC，
∴∠ACC=45°，
∴∠ABC=∠ACC+∠CCB=45°+20°=65°，
∴∠B=∠ABC=65°，
故答案为：B
【变式1-1】（2021九上·上高月考）如图，将△AOB绕着点O顺时针旋转70°，得到△COD，若∠COD=40°，则∠BOC的度数为（ ）
A．10°B．20°C．30°D．40°
【答案】C
【解答】解：∵将△AOB绕着点O顺时针旋转70°，得到△COD，
∴∠BOD=70°，
∵∠COD=40°，
∴∠BOC=∠BOD－∠COD=70°－40°=30°．
故答案为：C
【变式1-2】（2021九上·南充期末）如图，在 △ABC 中， ∠ACB=90° ， ∠A=30° ，将 △ABC 绕点C逆时针旋转90°得到 △DEC ，则 ∠AED 的度数为（ ）
A．105°B．120°C．135°D．150°
【答案】B
【解答】解：由旋转的性质可得：∠A=∠D=30°，∠ACB=∠DCE=90° ，
∴∠AED=∠D+∠DCE=120° ；
故答案为：B.
【变式1-3】（2021九上·澄海期末）如图，将△ABC绕点A按逆时针方向旋转得到△ABC．若点B刚好落在BC边上，且AB=CB'，若∠C=20°，则△ABC旋转的角度为（ ）
A．60°B．80°C．100°D．120°
【答案】C
【解答】解：∵AB=CB'，
∴∠B'AC=∠C，
由旋转前后对应线段相等可知：AB’=AB，
∴∠B=∠AB’B，
由三角形外角定理可知：∠AB’B=∠B’AC+∠C=2∠C=40°，
∴∠B=∠AB’B=40°，
∴△ABC旋转的角度为∠BAB’=180°-∠B-∠AB’B=180°-40°-40°=100°，
故答案为：C．
【变式1-4】（2021九上·庐江期末）如图，在△ABC中，∠BAC＝65°，∠C＝20°，将△ABC绕点A逆时针旋转n度（0＜n＜180）得到△ADE，若DE∥AB，则n的值为（ ）
A．65B．75C．85D．130
【答案】C
【解答】∵DE∥AB，
∴∠DAB＝180°－∠D，
∵∠D=∠B=180°－20°－65°=95°，
∴∠DAB=180°－95°=85°，
∴n=85°，
故答案为：C．
【典例2】（2021九上·道里期末）如图，在Rt△ABC中，∠C＝90°，∠ABC=30°，AC＝3，将Rt△ABC绕点A逆时针旋转得到Rt△AB'C'，连接BB'，则BB'的长度是（ ）
A．1B．3C．3D．23
【答案】D
【解答】解：∵在Rt△ABC中，∠C＝90°，∠ABC=30°，AC＝3，
∴∠BAC=90°－∠ABC=60°，AB=2AC=23，
∵将Rt△ABC绕点A逆时针旋转得到Rt△AB'C'，
∴∠BAB'=∠BAC=60°，AB=AB'，
∴△ABB'是等边三角形，
∴BB'=AB=23，
故答案为：D．
【变式2-1】（2021九上·香坊期末）如图，将RtΔABC绕点A按顺时针旋转一定角度得到RtΔADE，点B的对应点点D恰好落在边BC上，若AC=23，∠ABC=60°，则CD的长为（ ）
A．3B．2C．3D．1
【答案】B
【解答】解：∵AC=23，∠ABC=60°，∠BAC＝90°
∴∠C=90°-∠ABC=30°
∴BC＝2AB
∵BC2=AC2+AB2
∴AB＝2，BC＝2AB＝4，
∵Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，
∴AD＝AB，且∠B＝60°
∴△ADB是等边三角形
∴BD＝AB＝2，
∴CD＝BC−BD＝4−2＝2
故答案为：B．
【变式2-2】（2021秋•韶关期末）如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB＝3cm，则BE等于（ ）
A．2cmB．3cmC．4cmD．5cm
【答案】B
【解答】解：∵将△ABC绕点A顺时针旋转60°得到△AED，
∴AB＝AE＝3cm，∠BAE＝60°，
∴△ABE是等边三角形，
∴AB＝AE＝BE＝3cm，
故选：B
【变式2-3】（2021秋•邓州市期末）如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝1，将△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在AB边上，连结BB'，则△A'BB'的周长为（ ）
A．B．1+C．2+D．3+
【答案】D
【解答】解：∵∠ACB＝90°，∠A＝60°，AC＝1，
∴BC＝AC＝，AB＝2AC＝2，
∵△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在AB边上，
∴CA＝CA′，CB＝CB′，∠ACA′＝∠BAB′，
∵CA＝CA′，∠A＝60°，
∴△CAA′为等边三角形，
∴∠ACA′＝60°，AA′＝AC＝1，
∴A′B＝1，
∴∠BCB′＝60°，
∴△CBB′为等边三角形，
∴BB′＝CB＝，
∴△A'BB'的周长为A′B+AB′+BB′＝2+1+＝3+，
故选：D．
【典例3】（2021秋•岳池县期末）如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，连接OD，OA．
（1）求∠ODC的度数；
（2）试判断AD与OD的位置关系，并说明理由；
（3）若OB＝2，OC＝3，求AO的长（直接写出结果）．
【答案】（1）∠ODC＝60° （2）AD⊥OD （3）
【解答】解：（1）由旋转的性质得，CD＝CO，∠ACD＝∠BCO，
∴∠ACD+∠ACO＝∠BCO+∠ACO，即∠DCO＝∠ACB，
∵三角形ABC是等边三角形，
∴∠ACB＝60°，
∴∠DCO＝60°，
∴△OCD为等边三角形，
∴∠ODC＝60°；
（2）AD与OD的位置关系是：AD⊥OD，理由如下：
由（1）知∠ODC＝60°，
∵将△BOC绕点C按顺时针方向旋转一定的角度，得到△ADC，
∴∠ADC＝∠BOC＝150°，
∴∠ADO＝∠ADC﹣∠ODC＝90°，
∴AD⊥OD；
（3）由旋转的性质得，AD＝OB＝2，
∵△OCD为等边三角形，
∴OD＝OC＝3，
在Rt△AOD中，由勾股定理得：AO＝＝＝．
【变式3-1】（2021九上·中山期末）如图，在Rt△ABC中，∠C＝90°，将△ABC绕着点B逆时针旋转得到△FBE，点C，A的对应点分别为E，F．点E落在BA上，连接AF．
（1）若∠BAC＝40°，求∠BAF的度数；
（2）若AC＝8，BC＝6，求AF的长．
【答案】（1）解：在Rt△ABC中，∠C=90°，∠BAC=40°，
∴∠ABC=50°，
∵将△ABC绕着点B逆时针旋转得到△FBE，
∴∠EBF=∠ABC=50°，AB=BF，
∴∠BAF=∠BFA=12（180°-50°）=65°
（2）解：∵∠C=90°，AC=8，BC=6，
∴AB=10，
∵将△ABC绕着点B逆时针旋转得到△FBE，
∴BE=BC=6，EF=AC=8，
∴AE=AB-BE=10-6=4，
∴AF=AE2+EF2=42+82=45．
【变式3-2】（2021九上·谷城期中）如图，P是正三角形ABC内的一点，且PA＝6，PB＝8，PC＝10，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数．
【答案】解：∵△ABC为等边三角形，
∴AB=AC，∠BAC=60°，
∵△PAC绕点A逆时针旋转后，得到△P′AB，
∴AP′=AP，∠P′AP=∠BAC=60°，BP′=CP=10，
∴△AP′P为等边三角形，
∴P′P=AP=6，∠APP′=60°，
在△PBP′中，PP′=6，BP′=10，PB=8，
∵62+82=102，
∴P′P2+PB2=P′B2，
∴∠BPP′=90°，
∴∠APB=∠APP′+∠BPP′=60°+90°=150°．
故答案为6，150．
【考点2 利用旋转计算面积】
【典例4】（2021九上·鄞州月考）如图，在△ABC中，AB＝4，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分的面积为 .
【答案】4
【解答】解：∵在△ABC中，AB=4，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，∴△ABC≌△A1BC1，
∴A1B=AB=4，
∴△A1BA是等腰三角形，∠A1BA=30°，
∴SΔA1BA = 12 ×4×2=4.
又∵S阴影= SΔA1BA + SΔA1BC1 ﹣S△ABC， SΔA1BC1 =S△ABC，
∴S阴影= SΔA1BA =4.
故答案为：4.
【变式4-1】（2022•瑞金市模拟）如图，将边长为的正方形绕点B逆时针旋转30°，那么图中阴影部分的面积为（ ）
A．3B．C．D．
【解答】解：设C'D'与AD交于M，连接BM，如图：
∵边长为的正方形绕点B逆时针旋转30°，
∴AB＝BC'，∠A＝∠C'＝90°，∠CBC'＝30°，
∵BM＝BM，
∴△ABM≌△C'BM（HL），
∴∠ABM＝∠C'BM＝30°，
在Rt△ABM中，
AM＝＝1，
∴S△ABM＝AB•AM＝＝S△BC'M，
∴S阴影＝（）2﹣S△ABM﹣S△BC'M＝3﹣，
故选：C．
【变式4-2】（2021秋•丰泽区校级期末）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2．将△ABC绕点C按顺时针方向旋转到点D落在AB边上，此时得到△EDC，斜边DE交AC边于点F，则图中阴影部分的面积为（ ）
A．3B．1C．D．
【解答】解：∵△ABC是直角三角形，∠ACB＝90°，∠A＝30°，BC＝2，
∴∠B＝60°，AC＝BC＝2×＝2，AB＝2BC＝4，
∵△EDC是△ABC旋转而成，
∴BC＝CD＝AB＝2，
∵∠B＝60°，
∴△BCD是等边三角形，
∴∠BCD＝60°，
∴∠DCF＝30°，∠DFC＝90°，即DE⊥AC，
∴DE∥BC，
∵BD＝AB＝2，
∴DF是△ABC的中位线，
∴DF＝BC＝×2＝1，CF＝AC＝×2＝，
∴S阴影＝DF×CF＝×1×＝，
故选：D．
【变式4-3】（2021秋•南丹县期末）如图，边长相等的两个正方形ABCD和OEFG，若将正方形OEFG绕点O按逆时针方向旋转120°，两个正方形的重叠部分四边形OMCN的面积（ ）
A．不变B．先增大再减小
C．先减小再增大D．不断增大
【解答】解：∵四边形ABCD和四边形OEFG是正方形，
∴OB＝OC，∠BOC＝∠MON＝90°，∠OBC＝∠OCD＝45°，
∴∠BOM＝∠CON，
在△BOM和△CON中，
，
∴△BOM≌△CON（ASA），
∴S△BOM＝S△CON，
∴两个正方形的重叠部分四边形OMCN的面积为S△BOC＝S正方形ABCD，
故选：A
【考点3 坐标系中图形旋转的规律】
【典例5】（2021秋•阳东区期末）如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2020次得到正方形OA2020B2020C2020，如果点A的坐标为（1，0），那么点B2020的坐标为（ ）
A．（﹣1，1）B．C．（﹣1，﹣1）D．
【答案】C
【解答】解：∵四边形OABC是正方形，且OA＝1，
∴B（1，1），
连接OB，
由勾股定理得：OB＝，
由旋转得：OB＝OB1＝OB2＝OB3＝…＝，
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，
相当于将线段OB绕点O逆时针旋转45°，依次得到∠AOB＝∠BOB1＝∠B1OB2＝…＝45°，
∴B1（0，），B2（﹣1，1），B3（﹣，0），B4（﹣1，﹣1），…，
发现是8次一循环，所以2020÷8＝252…4，
∴点B2020的坐标为（﹣1，﹣1）
故选：C．
【变式5-1】（2021九上·惠来月考）如图，在正方形ABCD中，顶点A，B，C，D在坐标轴上，且B(2，0)，以AB为边构造菱形ABEF．将菱形ABEF与正方形ABCD组成的图形绕点O逆时针旋转，每次旋转45°，则第2020次旋转结束时，点F2020的坐标为（ ）
A．(−2，22) B．(−2，−22) C．(22，−2) D．(−22，−2)
【答案】D
【解答】∵点B的坐标为(2，0)，
∴OB=2，
由正方形的性质，得OA=2，
∴AB=22+22=22，
∵四边形ABEF为菱形，
∴AF=AB=22，
∴F(22，2)，
由题，可知旋转为每8次一个循环，2020÷8=252⋯4，
∴第2020次旋转结束时，点F2020与点F关于原点对称，
∴F2020(−22，−2)，
故答案为：D．
【变式5-2】（2021•张家界）如图，在平面直角坐标系中，将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2019次得到正方形OA2019B2019C2019，那么点A2019的坐标是（ ）
A．（，﹣）B．（1，0）C．（﹣，﹣）D．（0，﹣1）
【答案】A
【解答】解：∵四边形OABC是正方形，且OA＝1，
∴A（0，1），
∵将正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1，
∴A1（，），A2（1，0），A3（，﹣），…，
发现是8次一循环，所以2019÷8＝252…余3，
∴点A2019的坐标为（，﹣）
故选：A．
【变式5-3】（2021秋•郧阳区期末）如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…，若点A（3，0），B（0，4），则点B2021的横坐标为（ ）
A．12120B．12128C．12123D．12125
【答案】B
【解答】解：∵点A（3，0），B（0，4），
∴OA＝3，OB＝4，
∴AB＝＝5，
∴OA+AB1+B1C2＝3+5+4＝12，
观察图象可知，点B2020的纵坐标为4，
∵2020÷2＝1010，
∴点B2020的横坐标为1010×12＝12120，
12120+3+5＝12128
∴点B2021的坐标为（12128，0）．
故选：B．
夯实基础
1．（2021九上·海曙期末）如图， 在 △ABC 中， ∠BAC=75∘ ， 以点 A 为旋转中心， 将 △ABC 绕点 A 逆时针旋转得到 △ADE ， 点 B、C 的对应点分别为 D、E ， 连接 CE ， 若 CE//AB ， 则 ∠CAE 的值是( )
A．25∘B．30∘C．35∘D．45∘
【答案】B
【解答】解：∵CE∥AB，
∴∠BAC=∠ACE=75°；
∵ 以点 A 为旋转中心， 将 △ABC 绕点 A 逆时针旋转得到 △ADE ，
∴AE=AC，
∴∠AEC=∠ECA=75°；
∴∠CAE=180°-2×75°=30°.
故答案为：B.
2．（2021九上·虎林期末）如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1cm，将Rt△ABC绕点A逆时针旋转得到Rt△ABC，使点C落在AB边上，连接BB，则BB的长度是（ ）
A．1cmB．2cmC．3cmD．23cm
【答案】B
【解答】解：∵∠C=90°，∠ABC=30°，AC=1cm，
由直角三角形中，30°角所对的直角边等于斜边的一半可知，
∴AB=2AC=2cm，
又∠CAB=90°-∠ABC=90°-30°=60°，
由旋转的性质可知：∠CAB=∠BAB'=60∘，且AB=AB'，
∴ΔBAB'为等边三角形，
∴BB'=AB=2．
故答案为：B．
3．（2022春•泗县期中）如图所示，△ABC为直角三角形，BC为斜边，将△ABP绕点A逆时针旋转后，能与△ACP'重合．如果AP＝3，那么PP'的长等于（ ）
A．B．C．3D．4
【答案】A
【解答】解：∵△ABC是直角三角形，
∴∠BAC＝90°，
∵△ABP绕点A逆时针旋转后，能与△ACP′重合，
∴AP＝AP′，AB＝AC，∠PAP′＝∠BAC＝90°，
∴△APP′为等腰直角三角形，
∴PP′＝AP＝3，
故选：A．
4．（2021秋•甘井子区期末）如图，Rt△ABC中，∠ABC＝90°，∠BAC＝60°，AB＝1，将△ABC绕点B顺时针旋转得到△A'BC'，若直线A'C'经过点A，则CC'的长为（ ）
A．1B．2C．D．4
【答案】C
【解答】解：∵将△ABC绕点B顺时针旋转得到△A'BC'，
∴BA＝BA'，BC＝BC'，∠BAC＝∠BA'C'，
∵∠BAC＝60°，
∴∠A'＝60°，
∴△ABA'是等边三角形，
∴∠ABA'＝60°，
∴∠CBC'＝∠ABA'＝60°，
∴△BCC'是等边三角形，
∴CC'＝BC，
∵∠ABC＝90°，∠BAC＝60°，
∴∠ACB＝30°，
∴AC＝2AB＝2，
∴BC＝，
∴CC'＝BC＝，
故选：C
5（2022·呼和浩特）如图，△ABC中，∠ACB=90°，将△ABC绕点C顺时针旋转得到△EDC，使点B的对应点D恰好落在AB边上，AC、ED交于点F．若∠BCD=α，则∠EFC的度数是（用含α的代数式表示）（ ）
A．90°+12αB．90°−12αC．180°−32αD．32α
【答案】C
【解答】解：∵将△ABC绕点C顺时针旋转得到△EDC，且∠BCD=α
∴BC=DC，∠ACE=α，∠A=∠E，
∴∠B=∠BDC，
∴∠B=∠BDC=180°−α2=90°−α2，
∴∠A=∠E=90°−∠B=90°−90°+α2=α2，
∴∠A=∠E=α2，
∴∠EFC=180°−∠ACE−∠E=180°−α−α2=180°−32α，
故答案为：C．
6．（2021九上·富裕期末）如图，点D是等边△ABC内一点，AD＝3，BD＝3，CD＝32，△ACE是由△ABD绕点A逆时针旋转得到的，则∠ADC的度数是（ ）
A．40°B．45°C．105°D．55°
【答案】C
【解答】解：连接DE，如图：
∵ΔABC是等边三角形，
∴AB=AC，∠BAC=60°
∴∠BAD+∠CAD=60°
由旋转可得，ΔBAD≅ΔCAE
∴∠CAE=∠BAD，AD=AE=3，CE=BD=3
∴∠CAE+∠CAD=60°，即∠DAE=60°
∴ΔDAE是等边三角形，
∴DE=AD=3，∠ADE=60°
∵DE＝3，CE＝3，CD＝32，
∴DE2=9，CE2=9，CD2=18
∴DE2+CE2=CD2
∴△CDE是等腰直角三角形，
∴∠CDE=45°
∴∠ADC=∠ADE+∠CDE=60°+45°=105°
故答案为：C
7．（2022·益阳）如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（ ）
A．①②③B．①②④C．①③④D．②③④
【答案】B
【解答】解：∵△ABC绕A点逆时针旋转50°得到△AB′C′，
∴BC＝B′C′．故①正确；
∵△ABC绕A点逆时针旋转50°，
∴∠BAB′＝50°，
∴∠B′AC＝∠BAB′−∠CAB＝50°-20°=30°，
∵∠AB′C′＝∠ABC＝30°，
∴∠AB′C′＝∠B′AC，
∴AC∥C′B′．故②正确；
在△BAB′中，
∵AB＝AB′，∠BAB′＝50°，
∴∠AB′B＝∠ABB′＝12（180°−50°）＝65°，
∴∠BB′C′＝∠AB′B＋∠AB′C′＝65°＋30°＝95°，
∴C′B′与BB′不垂直．故③错误；
在△ACC′中，AC＝AC′，∠CAC′＝50°，
∴∠ACC′＝12（180°−50°）＝65°，
∴∠ABB′＝∠ACC′，故④正确.
∴正确结论的序号为：①②④.
故答案为：B.
8.（2021九上·集贤期末）如图，在△ABC中，∠C＝36°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，且AB′＝CB′，则旋转角为 度．
【答案】36
【解答】解：根据题意，可得∠BAB为旋转角，
∵AB′＝CB′
∴∠C=∠CAB=36°
∴∠ABB=2∠C=72°
由旋转的性质可得：AB=AB
∴∠B=∠ABB=72°
∴∠BAB=36°
故答案为：36
9．（2022春•通道县期末）已知，正方形ABCD的边长是4，正方形OMNE（OM＞AC）绕着正方形ABCD的对称中心O旋转，那么两正方形重叠部分的面积是 ．
【答案】4
【解答】解：如图：
∵四边形ABCD和四边形OENM都是正方形，
∴OD＝OC，∠ODP＝∠OCF＝45°，∠DOC＝∠EOM＝90°，
∴∠DOP＝∠COF．
在△PDO和△FCO中，
，
∴△PDO≌△FCO（ASA），
∴两正方形重叠部分的面积是等于△DOC的面积，
即重叠部分面积不变，总是等于正方形面积的，
∵正方形的边长为4，
∴正方形的面积为16，
∴重叠部分面积不变为．
故答案为：4．
10．（2022•新城区校级一模）如图，D是等边三角形ABC外一点，AD＝6，CD＝4，当BD长最大时，△ABC的面积为 ．
【答案】19
【解答】解：如图1，以CD为边作等边△DCE，连接AE．
∵BC＝AC，CD＝CE，∠BCA＝∠DCE＝60°，
∴∠BCD＝∠ACE，
在△BCD和△ACE中，
，
∴△BCD≌△ACE（SAS），
∴BD＝AE，
∵AE≤AD+DE，
当A、D、E三点共线时，AE＝AD+DE＝10，其值最大，
∴AE的最大值为10，
∴BD的最大值为10，
过点A作AF⊥BD于F，如下图，
∵△BCD≌△ACE，
∴∠BDC＝∠E＝60°，
∴∠ADF＝60°，
∵AF⊥BD，
∴∠DAF＝30°，
∴DF＝AD＝3，AF＝DF＝3，
∴BF＝10﹣3＝7，
∴AB2＝AF2+BF2＝76，
∴△ABC的面积＝AB2＝19，
故答案为：19
11.（2022春•高州市期末）如图，在△ABC中，AB＝8，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，则阴影部分面积为 ．
【答案】16
【解答】解：过A作AD⊥A1B于D，如图：
在△ABC中，AB＝8，将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1，
∴△ABC≌△A1BC1，
∴A1B＝AB＝8，
∴△A1BA是等腰三角形，∠A1BA＝30°，
∵AD⊥A1B，
∴AD＝AB＝4，
∴S△A1BA＝×8×4＝16，
又∵S阴影＝S△A1BA+S△A1BC1﹣S△ABC，且S△A1BC1＝S△ABC，
∴S阴影＝S△A1BA＝16，
故答案为：16．
12.（2021九上·互助期中）如图将 △ABC 绕点A逆时针旋转得到 △ADE ，点C和点E是对应点，若 ∠CAE=90° ， AB=1 ，求BD的长．
【答案】解：由旋转的性质得： AB=AD=1 ， ∠BAD=∠CAE=90° ，
∴BD=AB2+AD2=2 ．
13．如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.
（1）求证：△BDE≌△BCE；
（2）试判断四边形ABED的形状，并说明理由．
【答案】（1）证明：∵△BAD是由△BEC在平面内绕点B旋转60°而得，
∴DB=CB，∠ABD=∠EBC，∠ABE=60°，
∵AB⊥EC，
∴∠ABC=90°，
∴∠DBE=∠CBE=30°，
在△BDE和△BCE中，
∵DB=CB∠DBE=∠CBEBE=BE ，
∴△BDE≌△BCE；
（2）解：四边形ABED为菱形；由（1）得△BDE≌△BCE，∵△BAD是由△BEC旋转而得，∴△BAD≌△BEC，∴BA=BE，AD=EC=ED，又∵BE=CE，
∴四边形ABED为菱形
14.（涪陵期中）如图，P是正三角形ABC内的一点，且PA=5，PB=12，PC=13，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数．
【答案】解：∵△ABC为等边三角形，
∴AB=AC，∠BAC=60°，
∵△PAC绕点A逆时针旋转后，得到△P′AB，
∴∠P′AP=∠BAC=60°，AP′=AP，BP′=CP=13，
∴△AP′P为等边三角形，
∴PP′=AP=5，∠APP′=60°，
在△BPP′中，∵PP′=5，BP=12，BP′=13，
∴PP′2+BP2=BP′2，
∴△BPP′为直角三角形，∠BPP′=90°，
∴∠APB=∠APP′+∠BPP′=60°+90°=150°．
答：点P与点P′之间的距离为5，∠APB的度数为150°．
15．（2022春•渭滨区期末）如图，O是等边△ABC内一点，连接OA、OB、OC，且OA＝3，OB＝4，OC＝5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．
（1）求线段OD的长；
（2）求∠BDC的度数．
【解答】解：（1）∵△BAO绕点B顺时针旋转后得到△BCD，
∴BO＝BD，
而∠OBD＝∠ABC＝60°，
∴△OBD为等边三角形，
∴OD＝BO＝4；
（2）∵△BOD为等边三角形，
∴∠BDO＝60°，OD＝4，
∵△BAO绕点B顺时针旋转后得到△BCD，
∴CD＝AO＝3，
在△OCD中，CD＝3，OD＝4，OC＝5，
∵CD2+OD2＝32+42＝52＝OC2，
∴△OCD为直角三角形，∠ODC＝90°，
∴∠BDC＝∠BDO+∠ODC＝60°+90°＝150°．
16.（2022春•永丰县期中）如图，在△ABC中，BA＝BC，∠ABC＝40°，将△ABC绕点B按逆时针方向旋转110°，得到△DBE，连接AD，CE．
（1）求证：△ABD≌△CBE．
（2）求∠ACE的度数．
【解答】（1）证明：∵△ABC绕点B按逆时针方向旋转110°，
∴∠ABC＝∠DBE，∠ABD＝∠CBE，AB＝BC＝BD＝BE，
在△ABD与△CBE中，
，
∴△ABD≌△CBE（SAS）；
（2）解：∵∠ABD＝∠CBE＝110°，BA＝BC＝BD＝BE，
∴∠BAD＝∠ADB＝∠BCE＝∠BEC＝35°．
∵AB＝BC，∠ABC＝40°，
∴∠ACB＝70°，
∴∠ACE＝∠ACB+∠BCE＝105°．
能力提升
17．（2021九上·龙江期末）如图，在平面直角坐标系中，四边形ABOC是正方形，点A的坐标为（1，1），AA1⌢是以点B为圆心，BA为半径的圆弧；A1A2⌢是以点O为圆心，OA1为半径的圆弧，A2A3⌢是以点C为圆心，CA2为半径的圆弧，A3A4⌢是以点A为圆心，AA3为半径的圆弧，继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”，那么点A2021的坐标是 ．
【答案】（2021，0）
【解答】解：∵A点坐标为（1，1），且A1为A点绕B点顺时针旋转90°所得
∴A1点坐标为（2，0）
又∵A2为A1点绕O点顺时针旋转90°所得
∴A2点坐标为（0，-2）
又∵A3为A2点绕C点顺时针旋转90°所得
∴A3点坐标为（-3，1）
又∵A4为A3点绕A点顺时针旋转90°所得
∴A4点坐标为（1，5）
由此可得出规律：An为绕B、O、C、A四点作为圆心依次循环顺时针旋转90°，且半径为1、2、3、、n，每次增加1．
∵2021÷4=505…1
故A2021为以点B为圆心，半径为2021的A2020点顺时针旋转90°所得
故A2021点坐标为（2021，0）．
故答案为：（2021，0）．
18.（2021九上·黔西南期末）如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A1BO1的位置，使点A的对应点A1落在直线y＝33x上，再将△A1BO1绕点A1顺时针旋转到△A1B1Q2的位置，使点O1的对应点O2落在直线y＝33x上，依次进行下去…，若点A的坐标是（0，1），点B的坐标是（3，1），则点A12的横坐标是 .
【答案】9（3+1）
【解答】解：根据将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置可知：∠BA1O1＝90°，
∴∠OAB＝90°，
当y＝1时，x＝3，即AB＝3，
∴∠AOB＝60°，
如图，延长A2O2交x轴于E，则∠OEO2＝90°，
∴OO2＝2+3+1＝3+3，
∴O2E=3+32，
∴OE=OO22−O2E2=32（3+1），
∴点A2的横坐标为32（3+1），
同理可得：点A4的横坐标3（3+1），
点A6的横坐标92（3+1），
点A8的横坐标6（3+1），
∴点A12的横坐标是32×6（3+1），即9（3+1）.
故答案为：9（3+1）.
19．（2021九上·新乡期末）如图，△ABC的顶点A，B分别在x轴，y轴上，∠ABC＝90°，OA＝OB＝1，BC＝22，将△ABC绕点O顺时针旋转，每次旋转90°，则第2021次旋转结束时，点C的坐标为 .
【答案】（3，-2）
【解答】解：如图，过点C作CD⊥y轴于点D，
∵OA＝OB＝1，∠AOB=90°，
∴∠ABO=45°，
∵∠ABC＝90°，
∴∠CBD=45°，
∴∠BCD=45°，
∴BD=CD，
∵BC＝22，
∴BD2+CD2=BC2=(22)2 ，
∴BD=CD=2，
∴OD=OB+BD=3，
∴点C(2，3)，
将△ABC绕点O顺时针旋转，第一次旋转90°后，点C（3，-2），
将△ABC绕点O顺时针旋转，第二次旋转90°后，点C（-2，-3），
将△ABC绕点O顺时针旋转，第三次旋转90°后，点C（-3，2），
将△ABC绕点O顺时针旋转，第四次旋转90°后，点C（2，3），
⋯⋯
由此发现，△ABC绕点O顺时针旋转四次一个循环，
∵2021÷4=55⋯⋯1 ，
∴第2021次旋转结束时，点C的坐标为（3，-2）.
故答案为：（3，-2）