北师大版七年级下册4 用尺规作三角形课后作业题

这是一份北师大版七年级下册4 用尺规作三角形课后作业题，共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．如图，用直尺和圆规作一个三角形O1A1B1，使得O1A1B1≌OAB的示意图，依据（ ）定理可以判定两个三角形全等
A．SSSB．SASC．ASAD．AAS
2．如图，用直尺和圆规作两个全等三角形，能得到△COD≅△C′O′D′的依据是（ ）
A．B．C．D．
3．根据下列己知条件，能画出唯一的的是（ ）
A．，，B．，，
C．，，D．，，
4．已知三角形的两边及夹角，求作这个三角形时，第一步应（ ）
A．作一条线段等于已知线段
B．作一个角等于已知角
C．作两条线段等于已知线段并使其夹角等于已知角
D．先作一条线段等于已知线段或先作一个角等于已知角
5．如图，小明书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）
A．B．C．D．
6．已知线段，，，求作：，使，，．下面的作图顺序正确的是（ ）
①以点为圆心，以为半径画弧，以点为圆心，以为半径画弧，两弧交于点；
②作线段等于；
③连接，，则就是所求作图形．
A．①②③B．③②①C．②①③D．②③①
7．如图，△ABC为等边三角形，要在△ABC外部取一点D，使得△ABC和△DBC全等，下面是两名同学做法：
甲：①作∠A的角平分线l；
②以B为圆心，BC长为半径画弧，交l于点D，点D即为所求；
乙：①过点B作平行于AC的直线l；
②过点C作平行于AB的直线m，交l于点D，点D即为所求．
A．两人都正确B．两人都错误
C．甲正确，乙错误D．甲错误，乙正确
二、填空题
8．已知线段a，b，c，求作，使．
①以点B为圆心，c的长为半径画弧；
②连接；
③作；
④以点C为圆心，b的长为半径画弧，两弧交于点A．
作法的合理顺序是__________．
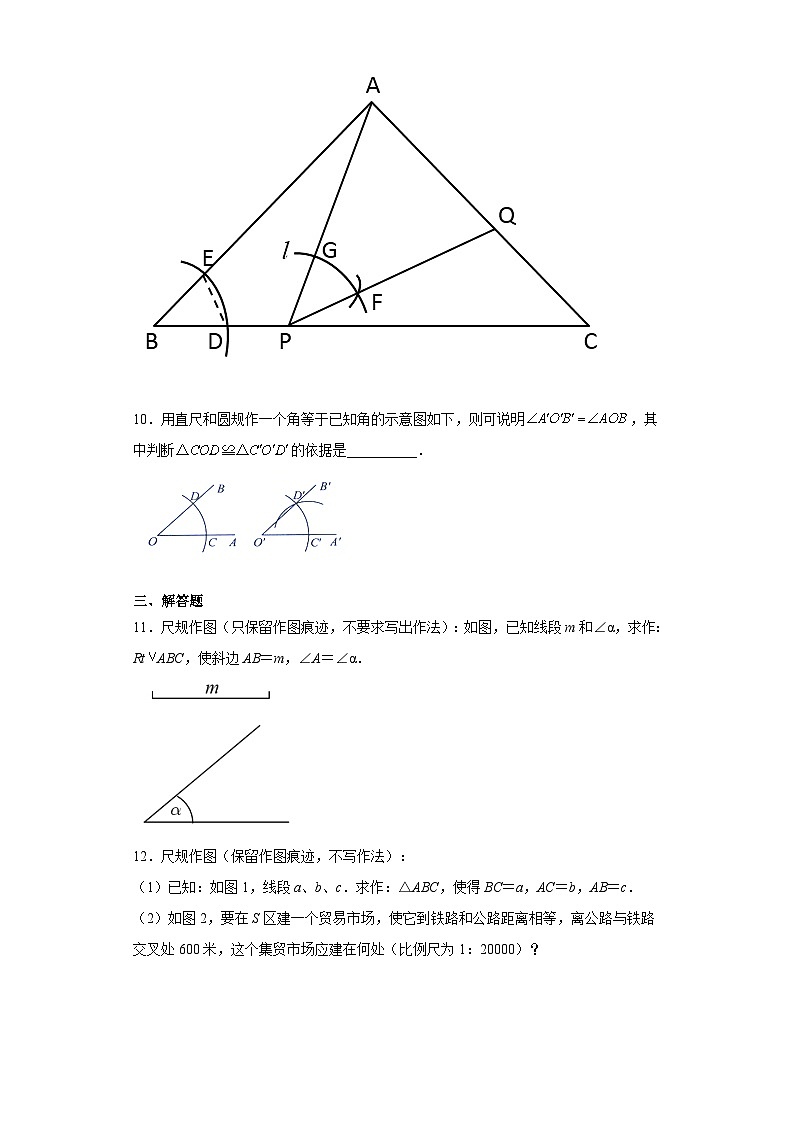
9．如图，在等腰直角三角形中，．点P在边上(不与B，C重合)，连结．按以下步骤作图：①以点B为圆心，适当长为半径作弧，分别交于点D，E．②以点P为圆心，长为半径作弧l，交于点G，③以点G为圆心，长为半径作弧，交弧l于点F，④过点P，F作射线交于点Q．若为等腰三角形，则的长为________．
10．用直尺和圆规作一个角等于已知角的示意图如下，则可说明，其中判断的依据是__________．
三、解答题
11．尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知线段m和∠α，求作：RtABC，使斜边AB＝m，∠A＝∠α．
12．尺规作图（保留作图痕迹，不写作法）：
（1）已知：如图1，线段a、b、c．求作：△ABC，使得BC＝a，AC＝b，AB＝c．
（2）如图2，要在S区建一个贸易市场，使它到铁路和公路距离相等，离公路与铁路交叉处600米，这个集贸市场应建在何处（比例尺为1：20000）？
13．作图题（要求：用尺规作图，不写作法，保留作图痕迹）．
已知：∠α，∠β，线段c．
求作：ABC，使∠A＝∠α，∠ABC＝∠β，AB＝2c．
14．如图，已知△ABC，求作：△OMN，使∠MON＝∠ABC，OM＝BC，MN＝AC．（保留作图痕迹，不必写作法）
参考答案
1．A
【分析】
根据尺规作图－作已知三角形以及全等三角形的判定定理可得结论．
【详解】
解：用直尺和圆规作一个三角形O1A1B1，
在一条直线上取一点，以点为圆心，为半径作弧，
与直线交于点，
∴，
以为圆心，为半径作弧，
以为圆心，为半径作弧，
两弧交于点，
∴，，
∴O1A1B1≌OAB依据的是“边边边”，
故选：A．
【点睛】
本题考查了尺规作图－作已知三角形以及全等三角形的判定定理，熟练掌握作图方式以及全等三角形的判定定理是解本题的关键．
2．B
【分析】
利用作法可确定OD=OD′=OC=OC′，CD=C′D′，然后根据全等三角形的判定方法可判断△COD≌△C'O'D'．
【详解】
解：由作法得OD=OD′=OC=OC′，CD=C′D′，
所以可根据“SSS”证明△COD≌△C'O'D'．
故选：B．
【点睛】
本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．也考查了全等三角形的判定．
3．C
【分析】
根据两个三角形全等的三个判定定理逐项判断即可完成．
【详解】
A、此三条线段不能围成一个三角形，故不能画出；
B、已知两边的长和其中AB边的对角，根据全等三角形的判定方法是不能画出三角形；
C、已知两个角和这两个角的夹边，根据ASA判定定理可以画出三角形；
D、已知三个角，根据两个三角形全等的判定方法，可心画出这个三角形，但画出的这样的三角形有无数个，故不合题意；
故唯一可以画出三角形的只有选项C符合题意；
故选：C．
【点睛】
本题考查了全等三角形的判定定理，掌握三个判定定理是关键．
4．D
【详解】
解析：已知三角形的两边及夹角，求作这个三角形时，第一步作一条线段等于已知线段，再以线段的一个端点为顶点作一个角等于已知角，或先作一个角等于已知角，然后在角的两边截取线段等于已知线段，再连接两交点．
答案：D
题型解法：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
5．C
【分析】
根据全等三角形的判定方法解答即可．
【详解】
解：画一个三角形A′B′C′，使∠A′=∠A，A′B′=AB，∠B′=∠B，
符合全等三角形的判定定理ASA，
故选：C．
【点睛】
本题考查了全等三角形的应用，熟练掌握三角形全等的判定方法是解题的关键．
6．C
【分析】
先画，确定、点位置，然后通过画弧确定点位置，从而得到．
【详解】
②先作线段等于，①再以点A为圆心，以为半径画弧，以点为圆心，以为半径画弧，两弧交于点，③然后连接，，则就是所求作图形．
故选：C．
【点睛】
本题考查了作图，作一个三角形，使这个三角形的三边等于已知的三条线段，其实质是作一条线段等于已知线段，原理是全等三角形的边边边判定定理．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图问题分解成基本作图来解决．
7．A
【分析】
根据题意先画出相应的图形，然后根据题意进行推理即可得到哪个正确哪个错误，本题得以解决．
【详解】
（甲）如图一所示，
∵△ABC为等边三角形，AD是∠BAC的角平分线，
∴∠BEA=90°，
∴∠BED=90°，
∴∠BEA=∠BED=90°，
由甲的作法可知，AB=BD，
∴∠ABC=∠DBC，
在△ABC与△DBC中，，
∴△ABC≌△DBC，
故甲的作法正确；
（乙）如图二所示，
∵BD∥AC，CD∥AB，
∴∠ACB=∠DBC，∠ABC=∠DCB，
在△ABC和△DCB中，，
∴△ABC≌△DCB（ASA），
∴乙的作法是正确的．
故选A．
【点睛】
本题考查作图-复杂作图，全等三角形的判定，解题的关键是明确题意，作出相应的图形，进行合理的推理证明．
8．③①④②
【分析】
根据作三角形的步骤：第一步先作一条线段等于三角形的一边，第二步以已作的线段的两个端点为圆心，以对应的长为半径画弧确定交点位置，最后顺次连接即可，由此进行判断即可．
【详解】
解：先作，再以点B为圆心，c的长为半径画弧；接着以点C为圆心，b的长为半径画弧，两弧交于点A，然后连接，则即为所求．
故答案为：③①④②．
【点睛】
本题主要考查了用尺规作图—作三角形的步骤，解题的关键在于能够熟练掌握相关知识进行求解．
9．或
【分析】
根据尺规作图可知∠APQ=∠B=45°，因为为等腰三角形，因此有三种情况，（1）当AP=AQ时，(2)当AP=PQ时，（3）当AQ=PQ时，进而利用等量关系得出答案；
【详解】
解： ∵
∴∠C=∠B=45°,BC=
由作图步骤可得：∠APQ=∠B=45°，
∵为等腰三角形
∴有三种情况
（1）当AP=AQ时
∵AP=AQ，∠APQ=∠B=45°
∴∠APQ=∠AQP=45°
∴∠PAQ=90°
∵∠BAC=90°
∴P和B点重合不符合题意；
（2）当AP=PQ时，∠APQ=∠B=45°
∴∠PAQ=∠AQP=（180°-45°）÷2=67.5°
∵∠C=45°
再△APC中，∠APC=180°-∠C-∠PAQ=67.5°
∴∠PAQ=∠APC=67.5°
∴AC=PC=1
∴BP=BC-PC=
(3) ）当AQ=PQ时，∠APQ=∠B=45°
∴∠APQ=∠PAQ=45°
∴∠BAP=∠PAQ=45°
∴AP为BC的垂直平分线
∴BP=BC=
故答案：或
【点睛】
本题考查作图-基本作图,等腰三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
10．
【解析】
【分析】
利用作法得到△C'O'D'和△COD的三边对应相等，从而根据SSS可证明△C'O'D'≌△COD，然后根据全等三角形的性质得到∠A'0'B'=∠A0B.
【详解】
解：由作法得0D=0C=0D'=OC'，CD=C'D'，则根据“SSS”可判断△C'O'D≌△COD，所以∠A'0'B'=∠A0B.
故答案：SSS.
【点睛】
本题考查了作图-基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）.也考查了角平分线的性质定理的逆定理.
11．见解析
【分析】
①作∠A=∠； ②在∠A的一边上截取AB=m； ③过B作∠A的另一边的垂线，垂足为C， 根据以上步骤逐一作图即可.
【详解】
解：如图，即为所求作的三角形，
【点睛】
本题考查的是已知斜边和一锐角求作直角三角形，掌握利用尺规作一个角等于已知角，过一点作已知直线的垂线是解题的关键.
12．（1）见解析；（2）地图上的集贸市场应在铁路和公路形成的角（S区）的角平分线上，且与点O的距离为3cm．
【分析】
（1） ①如图，作射线BM，在射线BM上截取BA=c，分别以B，A为圆心，a，b为半径作弧，两弧交于点C，连接BC，AC，△ABC即为所求；②利用尺规作出∠AOB的射线OC即可．
（2） 利用角的平分线上的点到角的两边的距离相等可知集贸市场在公路、铁路相交的角平分线上，再根据比例尺计算出集贸市场离O的距离即可．
【详解】
（1）如图，△ABC即为所求．
（2） 如图所示：
设集贸市场距离交点O为xm，则：
，
解得：x=0.03，
0.03m=3cm．
OP=3cm．
点P即为所求，地图上的集贸市场应在铁路和公路形成的角（S区）的角平分线上，且与点O的距离为3cm．
【点睛】
考查了复杂作图和角平分线的性持，解题关键关键是掌握基本作图的方法，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作和掌握角平分线上的点到角两边的距离相等．
13．见解析
【分析】
先做射线AM，再以点A为顶点作∠A＝∠α，在AM上截取AB，使AB＝2c，最后以点B为顶点作做∠ABC＝∠β即可
【详解】
解：△ABC即为所求作的三角形．

【点睛】
本题主要考查了三角形的一些基本作法,解题的关键是熟练掌握五种基本作图，属于中考常考题型．
14．见解析
【分析】
先作∠POQ=∠∠ABC，然后在射线OQ上作线段OM=BC，再以M为圆心,AC长为半径，画弧交OP于点N1、N2，则△OMN1、△OMN2即为所求三角形，即可求解．
【详解】
解：1、先作∠POQ=∠∠ABC，
2、在射线OQ上作线段OM=BC，
3、以M为圆心,AC长为半径，画弧交OP于点N1、N2