



湖北省武汉市第三寄宿中学2022-2023学年七年级下学期月考数学试题(原卷版+解析版)
展开1. 下列各数中,不是无理数的是( )
A. B. C. D.
2. 下列四幅图案能通过基本图形平移得到的是( )
A. B. C. D.
3. 如图,,,垂足分别为A、D,则图中表示点C到直线距离的线段是( )
A. B. C. D.
4. 下列各点在第二象限的是( )
A. B. C. D.
5. 用式子表示“9的平方根”正确的是( )
A. B. C. D.
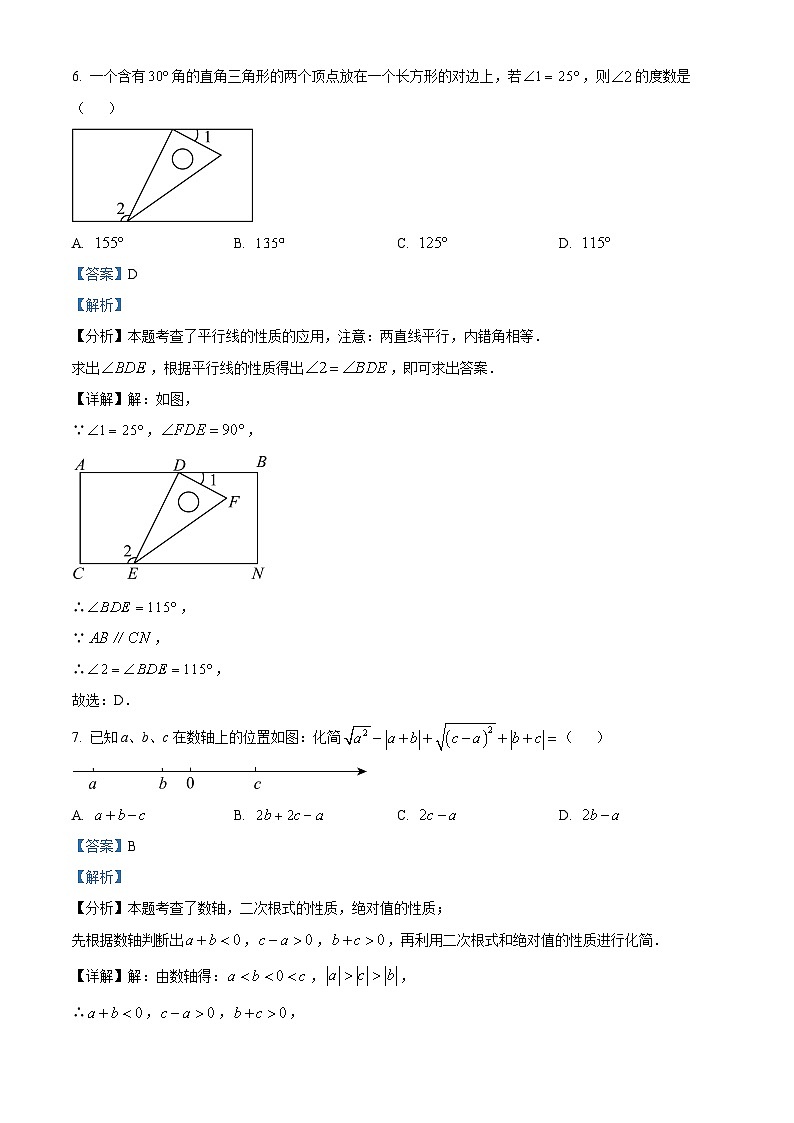
6. 一个含有角直角三角形的两个顶点放在一个长方形的对边上,若,则的度数是( )
A. B. C. D.
7. 已知a、b、c在数轴上的位置如图:化简( )
A. B. C. D.
8. 点P为直线m外一点,A,B,C为直线m上三点,,,,点P到直线m距离可能是( )
A. 5B. 6C. D.
9. 下列语句:①若两个数平方后相等,则这两个数也一定相等;②相等的角是对顶角;③两直线平行,内错角互补;④垂线段最短;⑤若,则,其中是命题的个数是( )
A. 2B. 3C. 4D. 5
10. 已知,,的平方根是( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11. 计算:______.
12. 将点先向右平移3个单位,再向上平移1个单位后,则得到点的坐标为______.
13. 已知,,,,按以上规律推算近似值是______.
14. “俄罗斯方块”是一款风靡全球的经典游戏,某局游戏当前情况如图所示,若上端小正方形移动最短的距离后能形成消除,则共有______种不同的移动方法.
15. 平面直角坐标系中,关于点,点的说法:①当时,点A在第二象限:②当时,三角形的面积为12;③当A,B两点在不同象限内时,必有;④点为y轴上一点,连接AC并延长至D,使,则D点坐标为.其中正确的结论是______(填写序号).
16. 边长为与的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积是______(取3).
三、解答题(本大题共8小题,共72分)
17. 计算:
(1)
(2)
18. 小明在研究:三角形的内角和为.这个命题时进行了以下操作,请你根据他的思路填写证明过程.
证明:过A点作______
∵(已知)
∴______,______( )
∵______( )
∴
∴______( )
19. 已知点
(1)当点P到两坐标轴的距离相等,点P的坐标为______.
(2)如果点M在第三象限,且点M到x轴距离为3,到y轴的距离为4,求点M的坐标.
20. 一块长方形空地面积为1500平方米,其长宽之比为.
(1)求这块长方形空地的周长;
(2)如图,在空地内修建“T字型”走道(横向走道宽度不变)后将空地分割成两个花坛(花坛1为正方形,花坛2为长方形,其长宽之比为),花坛的总面积为1176平方米,宽度为米的农药喷洒车能不能在走道上正常通行?
21. 如图,由小正方形构成的网格,每个小正方形的顶点叫做格点,仅用无刻度的直尺在给定网格中按要求画图.(保留连线痕迹,如有多个答案均要呈现)
(1)如图1,A,B,C均为格点,画线段由线段平移所得,使点A与点C重合,点B与点D重合;
(2)在图2中,A,B,C,F均为格点,
①直接写出三角形的面积为_____;
②画格点E(点E在直线右侧),使四边形的面积为20;
(3)在图3中,A,B,C,D均为格点,过点D作直线l平分三角形的面积.
22 阅读材料1.
是无理数,而无理数是无限不循环小数,因此的小数部分不能全部写出来,但由于,所以的整数部分为1,将减去其整数部分1,差就是小数部分,其小数部分为.
(1)直接写出的小数部分是______;的小数部分是______;
(2)已知,其中x是整数,且,求的值;
阅读材料2.
小明在查阅了乘法公式后,想出了一个估算无理数近似值的方法,例如求的近似值(结果精确到0.01),设,其中,则,因为,所以,所以,解得,所以.
(3)利用小明的方法估算的近似值(结果精确到0.01)
23. 【问题背景】如图1,,点P,Q位于两侧,连接,,,,直接写出①,,的数量关系为______;②,,的数量关系为______;
【尝试应用】如图2,在(1)的条件下,作,的角平分线交于点M,若与互补,试写出与的数量关系,并证明:(【问题背景】中相关结论可以直接使用)
【拓展创新】如图3,,点M,N位于左侧,作,的角平分线交于点P,;若,直接写出的度数是______.
24. 在平面直角坐标系中,点A的坐标为,点B的坐标
(1)如图1,若,求A,B两点的坐标;
(2)在(1)条件下,有一点,若三角形ABP的面积为12,求m的值;
(3)如图2,当,时,将点A向上移动2t个单位长度,将点B向右移动t个单位长度,取线段AB的中点C,过点C作于E,并延长CE至D,使,试求证为定值.
湖北省武汉市黄陂区祁家湾街道四黄中学2023-2024学年七年级下学期月考数学试题(原卷版+解析版): 这是一份湖北省武汉市黄陂区祁家湾街道四黄中学2023-2024学年七年级下学期月考数学试题(原卷版+解析版),文件包含精品解析湖北省武汉市黄陂区祁家湾街道四黄中学2023-2024学年七年级下学期月考数学试题原卷版docx、精品解析湖北省武汉市黄陂区祁家湾街道四黄中学2023-2024学年七年级下学期月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
湖北省武汉市第三寄宿中学2022-2023学年第一学期期末八年级数学试题: 这是一份湖北省武汉市第三寄宿中学2022-2023学年第一学期期末八年级数学试题,共10页。试卷主要包含了选择题,填空题,计算题等内容,欢迎下载使用。
湖北省武汉市第三寄宿中学2022—2023学年上学期期末八年级数学试题: 这是一份湖北省武汉市第三寄宿中学2022—2023学年上学期期末八年级数学试题,共10页。试卷主要包含了选择题,填空题,计算题等内容,欢迎下载使用。












