重庆市巴蜀中学2023-2024学年高一下学期3月月考数学试题（Word版附解析）

这是一份重庆市巴蜀中学2023-2024学年高一下学期3月月考数学试题（Word版附解析），文件包含重庆市巴蜀中学2023-2024学年高一下学期3月月考数学试题Word版含解析docx、重庆市巴蜀中学2023-2024学年高一下学期3月月考数学试题Word版无答案docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。
注意事项：
1．作答前､考生务必将自己的学校､班级､姓名､准考证号填写在答题卡的规定位置上．
2．作答时､务必将答案写在答题卡上，写在试卷及草稿纸上无效．
3．考试结束后，将答题卡交回，试卷自行保存．试卷满分150分，考试时长120分钟．
一､单选题：本题共8小题，每小题5分，共40分．在每个小题给出的四个选项中，只有一项是符合题目要求的．
1. 在中，角的对边分别为，若，则（ ）
A. B. C. D.
2. 已知向量满足：，则（ ）
A. 1B. 3C. D. 10
3. 在中，角对边分别为，若，则（ ）
A. B. 2C. D.
4. 在中，动点P满足，则P点轨迹一定通过的（ ）
A. 外心B. 内心C. 重心D. 垂心
5. 在中，角的对边分别为，若，且，则（ ）
A. B. C. D.
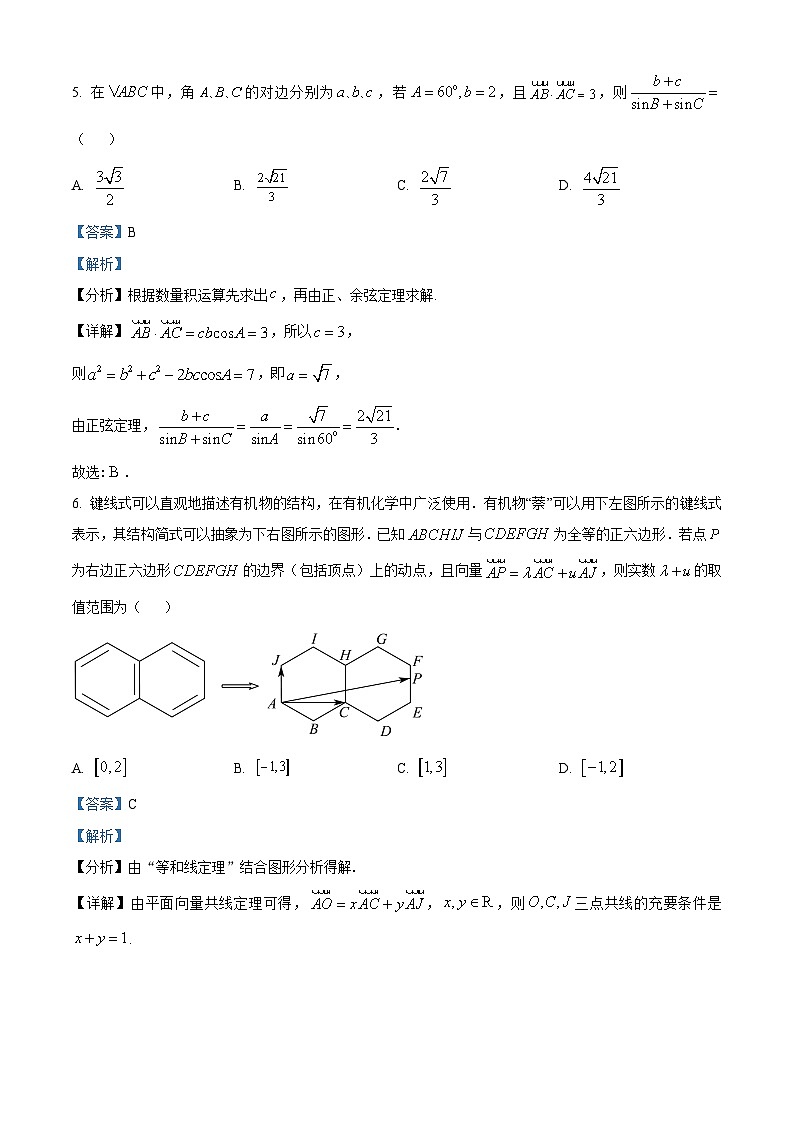
6. 键线式可以直观地描述有机物的结构，在有机化学中广泛使用．有机物“萘”可以用下左图所示的键线式表示，其结构简式可以抽象为下右图所示的图形．已知与为全等的正六边形．若点为右边正六边形的边界（包括顶点）上的动点，且向量，则实数的取值范围为（ ）
A. B. C. D.
7. 在中，角的对边分别为，若，又的面积，且，则（ ）
A. 64B. 84C. -69D. -89
8. 已知向量满足：为单位向量，且和相互垂直，又对任意不等式恒成立，若，则的最小值为（ ）
A. 1B. C. D.
二､多选题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．
9. 关于同一平面内的任意三个向量，下列四种说法错误的有（ ）
A.
B. 若，且，则
C. 若，则或
D.
10. 在中，角的对边分别为，且已知，则（ ）
A. 若，且有两解，则的取值范围是
B. 若，且恰有一解，则的取值范围是
C. 若，且为钝角三角形，则取值范围是
D. 若，且为锐角三角形，则的取值范围是
11. 在等腰中，已知，若分别为的垂心､外心､重心和内心，则下列四种说法正确的有（ ）
A. B.
C. D.
12. 在锐角中，已知角的对边分别为，且，，则下列说法正确的是有（ ）
A. 的外接圆的周长为
B. 的周长的取值范围为
C. 的面积的取值范围为
D. 的内切圆的半径的取值范围为
三､填空题：本题共4小题，每小题5分，共20分．
13. 已知平面向量与的夹角为锐角，则实数的取值范围是__________．
14. 抗战胜利纪功碑暨人民解放纪念碑，简称“解放碑”，位于重庆市渝中区解放碑商业步行街中心地带，是抗战胜利的精神象征，是中国唯一一座纪念中华民族抗日战争胜利的纪念碑．如图：在解放碑的水平地面上的点处测得其顶点的仰角为､点处测得其顶点的仰角为，若米，且，则解放碑的高度__________米．
15. 如图：在平行四边形中，为对角线与的交点，为直线与的交点，为直线与的交点，若，，且，则__________．
16. 在中，角所对边分别为，已知，若为边上的中线，且，则的面积等于__________．
四､解答题：本题共6小题，第17小题10分，其余小题每题12分，共70分．解答题应写出文字说明､证明过程或演算步骤．
17. 已知向量．
（1）若向量，求向量与向量夹角的大小；
（2）若向量，求向量在向量方向上的投影向量的坐标．
18. 在中，角的对边分别为，已知．
（1）求角的大小；
（2）若的面积为，角的平分线与交于点，且，求边的值．
19. 如图：在中，已知与交于点．

（1）用向量表示向量；
（2）过点作直线，分别交线段于点，设，若，，当取得最小值时，求模长．
20. 在中，角的对边分别为，若，又以为边长的三个正三角形的面积分别为，且．
（1）求的面积：
（2）若，求的周长．
21. 为改进城市旅游景观面貌､提高市民的生活幸福指数，城建部拟在以水源为圆心空地上，规划一个四边形形状的动植物园．如图：四边形内接于圆（注：圆的内接四边形的对角互补），为动物园区，为植物园区（为了方便植物园的植物浇水灌溉，水源必须在植物园区的内部或边界上）．又根据规划已知千米，千米．
（1）若，且，求边长为多少千米？
（2）若线段千米，求动植物园的面积（即四边形的面积）的最小值为多少平方千米？
22. 定义函数的“源向量”为，非零向量的“伴随函数”为，其中为坐标原点．
（1）若向量的“伴随函数”为，求在的值域；
（2）若函数的“源向量”为，且以为圆心，为半径的圆内切于正（顶点恰好在轴的正半轴上），求证：为定值；