第3章函数与基本初等函数第1节函数的概念及其表示2025届高考数学一轮总复习(适用于新高考新教材)ppt

展开

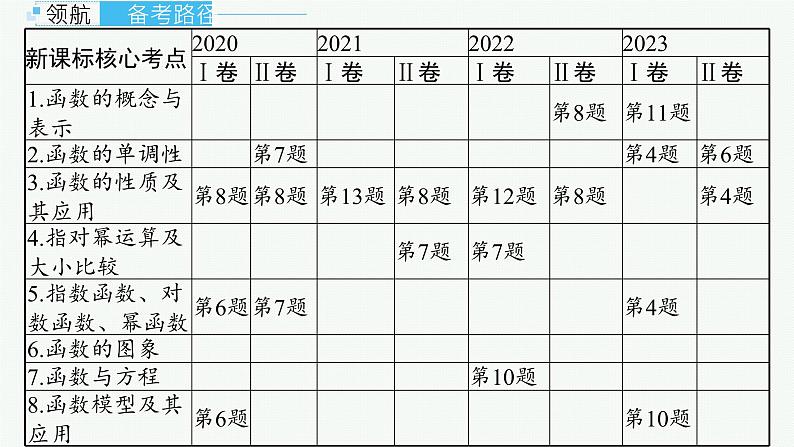
这是一份第3章函数与基本初等函数第1节函数的概念及其表示2025届高考数学一轮总复习(适用于新高考新教材)ppt，共38页。PPT课件主要包含了目录索引，函数的概念，实数集，任意一个数x，定义域，对应关系，解析式法，题组三连线高考等内容，欢迎下载使用。

考情分析:1.函数模块是高考考查的核心内容之一,主要以基本初等函数或者由基本初等函数组成的复合函数为载体,考查函数的定义域、值域、性质、图象、零点等相关知识,重点是函数的奇偶性、周期性与单调性等,常与导数、不等式、方程等交汇命题,考查数形结合、分类讨论、函数与方程等数学思想,以客观题的形式出现,难度中等,分值5分~10分.2.高考对函数知识的考查,重在交汇融合,还存在隐性考查,渗透在整张试卷中.
复习策略:1.明晰重要概念,熟练掌握常见基本初等函数的图象与性质:定义域、值域、最值、奇偶性、周期性、单调性、零点等概念是解决函数问题的基础,应明确二次函数、指数函数、对数函数、幂函数的图象与性质贯穿在解决函数问题的全过程,应熟练掌握.2.强化数学思想方法的训练:数形结合、函数与方程、分类讨论等数学思想方法在解决函数问题中具有重要应用,应强化应用意识.3.注重数学运算能力的提升:在解决函数问题的过程中,代数推理、变形化简、数值计算等贯穿其中,是解题成败的关键因素,因此在复习中应重视数学运算能力的训练与提升.4.善于运用函数性质的二级结论快速、简洁地解决相关问题.5.涉及抽象函数问题,注意寻找函数原型帮助分析和解决问题.
第1节函数的概念及其表示
研考点精准突破
强基础固本增分
2.函数的表示方法表示函数的常用方法有__________、图象法、列表法.
微思考直线x=a(a为常数)与函数f(x)的图象的交点个数是多少?
提示直线x=a(a为常数)与函数f(x)的图象的交点个数是1或0.若设f(x)的定义域为D,则当a∈D时,有1个交点,当a∉D时,有0个交点.
3.分段函数如果一个函数,在其定义域内,对于自变量的不同取值区间,有不同的对应关系,则称其为分段函数.
微点拨1.分段函数只是在定义域的不同区间上解析式不同,但它表示的是同一个函数.2.分段函数的定义域是各段区间的并集,值域是各段区间值域的并集.3.在解析式中含有绝对值的函数一般都可以化为分段函数.4.在分段函数的图象中,横坐标相同的点不能有两个或两个以上.
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.对于函数f:A→B,其值域是集合B.(　　)
题组二回源教材5.(人教B版必修第一册3.1.1节练习B第8题)已知函数f(x+1)=2x-3,求f(4),f(x).
解令x+1=4,得x=3,代入得f(4)=3;设x+1=t,则x=t-1,代入得f(t)=2t-5,因此f(x)=2x-5.
6.(人教A版必修第一册习题3.1第17题)探究是否存在函数f(x),g(x)满足条件:(1)定义域相同,值域相同,但对应关系不同;
解存在,例如f(x)=2x+1与g(x)=3x-1的定义域和值域均为R,但对应关系不同.
解存在,例如f(x)=x2,x∈R与g(x)=x2,x∈[0,+∞)的值域和对应关系相同,但定义域不同.
(2)值域相同,对应关系相同,但定义域不同.
(-∞,0)∪(0,1]
考点一函数的概念及应用
例1(1)(多选题)(2024·江西临川模拟)下列函数中,与函数y=2-x是同一函数的是(　　)
规律方法函数概念的应用技巧(1)判断两个函数是否为同一个函数,关键在于两点:一是定义域相同;二是对应关系相同.其中定义域要在解析式化简之前求得,在定义域的限制条件下可以对解析式进行化简.(2)函数定义中要求对于x 的每一个确定值,y 应有唯一的值与之对应,否则就不能确定函数关系,据此可通过取特殊值验证的方法判断给出的一个对应关系是否是函数.若存在x1, x2使得g(x1)=g(x2),但h(x1)≠h(x2),那么就不存在函数f(x)满足f(g(x))=h(x).(3)对于抽象函数的求值问题,一般采用赋值法,即通过将函数满足的等式中的变量取适当的值,即可获得特殊函数值之间的等量关系,从而求出相应的函数值
考点二函数的定义域
(3)(2024·江西南昌模拟)已知函数f(x)的定义域是(-1,3),则函数y=f(x+1)-lg(x-1)的定义域是__________.
规律方法函数定义域的求解方法(1)给定解析式的函数定义域的求法:①根据解析式有意义的条件列出自变量满足的不等式(组);②解不等式(组)的解集即为定义域;③注意不要轻易化简解析式,并且定义域必须写成集合或区间的形式.
(2)复合函数定义域的求法:
由题意可知上式的解集为[1,+∞),所以x=1为方程x2+2x+a=0的一个根,所以1+2+a=0,得a=-3,故选A.
考点三函数的解析式
例3根据下列条件求函数的解析式:(1)已知f(x)是一次函数,且满足3f(x)-2f(x-1)=2x+5,求f(x)的解析式;
(2)已知函数f(x)满足f(cs x-1)=cs 2x-1,求f(x)的解析式;
解依题意设f(x)=ax+b(a≠0),则由3f(x)-2f(x-1)=2x+5可得3(ax+b)-2[a(x-1)+b]=2x+5,
解函数f(x)满足f(cs x-1)=cs 2x-1=2cs2x-1-1=2cs2x-2,设cs x-1=t,则cs x=t+1,由cs x∈[-1,1],知t∈[-2,0],故原函数可转化为f(t)=2(t+1)2-2=2t2+4t,t∈[-2,0],即f(x)的解析式为f(x)=2x2+4x(-2≤x≤0).
(4)已知f(x)+2f(-x)=x2+2x,求f(x)的解析式.
解因为f(x)+2f(-x)=x2+2x,①所以f(-x)+2f(x)=x2-2x,所以2f(-x)+4f(x)=2x2-4x,②
考点四分段函数(多考向探究预测)
考向1 分段函数的求值问题
所以f(f(-1))=f(2)=22=4,故选D.
解析当m≥0时,由f(m)=-m得m2+1=-m,此方程无实数解;当m<0时,由f(m)=-m得m2+4m=-m,解得m=-5,m=0(舍去),故实数m的值为-5.
解析当x>0时,由f(x)=f(x-2)得f(x)=f(x+2),即当x>0时,f(x)的周期为2,所以f(2 023)=f(2×1 010+1)=f(1),则f(1)=f(-1)=(-1)2+1=2.
规律方法分段函数求值问题的求解策略(1)已知自变量的值求函数值时,应先判断自变量的值属于哪一段区间,然后代入该段的解析式求值,当求f(f(a))的值时,应由内到外依次求值;(2)若分段函数某一段的解析式形如f(x)=f(x-m)(m ≠0)的形式,则应由此得出函数的周期,利用周期将自变量的值进行转化,然后代入另一段解析式求值;(3)已知函数值求自变量的值时,需要结合分段区间对自变量的值分类讨论,解方程求值,并注意求得的值需要满足自变量相应的取值范围,否则应舍去.
考向2 分段函数与不等式
(-∞,-3)∪(3,+∞)
变式探究1将本例中的不等式“f(x)<-3”改为“f(x)≥|x|”,则其解集为__________.
变式探究2将本例中的不等式“f(x)<-3”改为“f(f(x))<0”,则其解集为__________.
变式探究3将本例中的不等式“f(x)<-3”改为“f(x)+f(x-2)>0”,则其解集为__________.
解析当x>2时,不等式化为-x2+2x-(x-2)2+2(x-2)>0,即x2-4x+4<0,解得x∈⌀;当00,即x2-5x<0,解得00,即6x+6>0,解得-1

相关课件更多