数学八年级下册17.1 勾股定理练习

这是一份数学八年级下册17.1 勾股定理练习，共11页。试卷主要包含了勾股弦图，勾股树等内容，欢迎下载使用。
一、勾股弦图
1、（2020•绍兴）如图1，直角三角形纸片的一条直角边长为2，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为3的正方形中（纸片在结合部分不重叠无缝隙），则图2中阴影部分面积为 ．
2、如图是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若，，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是 ．
A
B
C
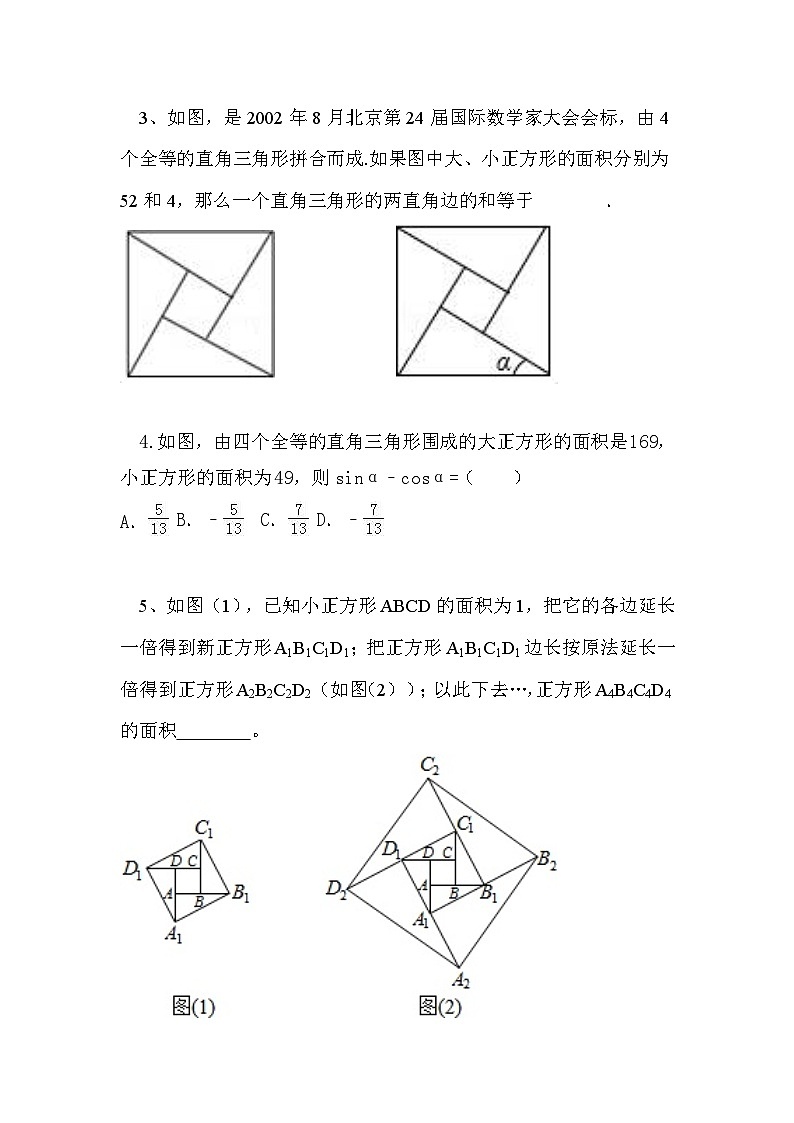
3、如图，是2002年8月北京第24届国际数学家大会会标，由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4，那么一个直角三角形的两直角边的和等于 ．

4.如图，由四个全等的直角三角形围成的大正方形的面积是169，小正方形的面积为49，则sinα﹣csα=（ ）
B．﹣C．D．﹣
5、如图（1），已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2（如图（2））；以此下去…，正方形A4B4C4D4的面积 。
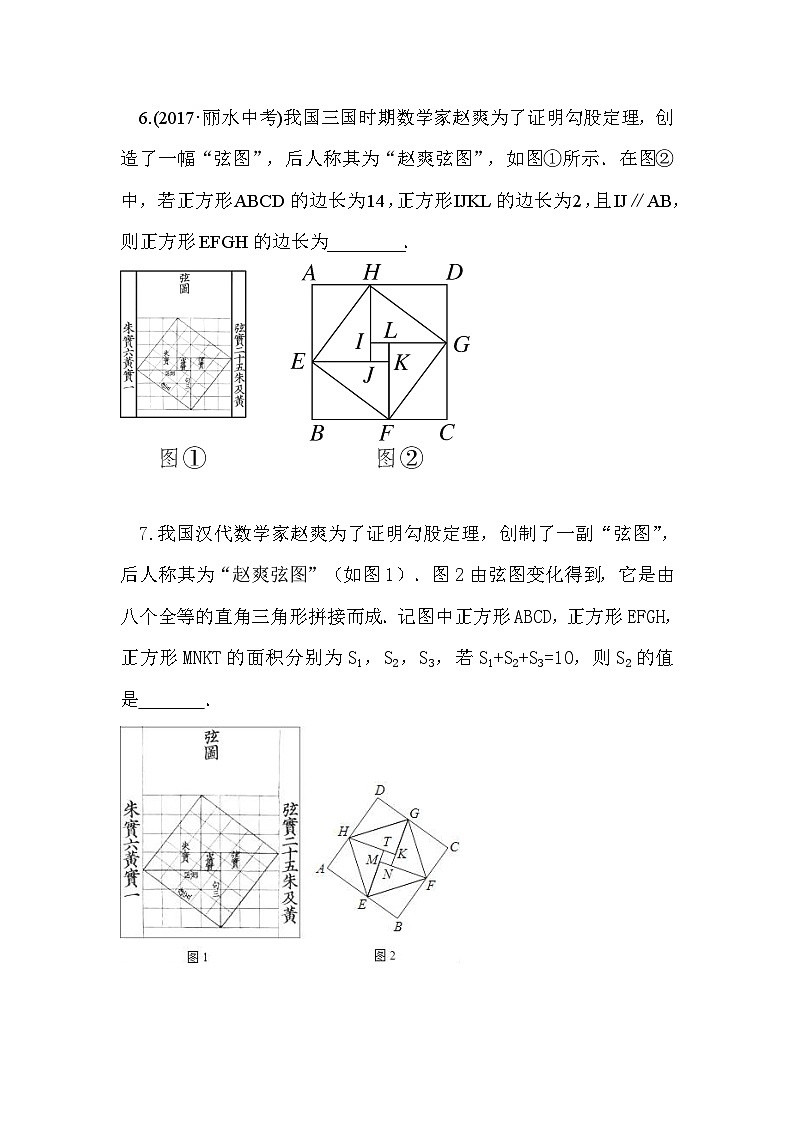
6.(2017·丽水中考)我国三国时期数学家赵爽为了证明勾股定理，创造了一幅“弦图”，后人称其为“赵爽弦图”，如图①所示．在图②中，若正方形ABCD的边长为14，正方形IJKL的边长为2，且IJ∥AB，则正方形EFGH的边长为________．
7.我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3=10，则S2的值是 ．
8.如图，在正方形ABCD中，AD=5,点E,F是正方形ABCD内两点，且AE=FC=3, BE=DF=4,则EF的长为（ ）
A．B．223C．75D．2
9、（2021·温州）由四个全等的直角三角形和一个小正方形组成的大正方形如图所示．过点作的垂线交小正方形对角线的延长线于点，连结，延长交于点．若，则的值为（ ）
A．B．C．D．
10、 如图是一个由5张纸片拼成的，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为，另两张直角三角形纸片的面积都为，中间一张矩形纸片的面积为，与相交于点O．当的面积相等时，下列结论一定成立的是（ ）
B. C. D.
如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1 ， 另两张直角三角形纸片的面积都为S2 ， 中间一张正方形纸片的面积为S3 ， 则这个平行四边形的面积一定可以表示为（ ）
A.4S1 B.4S2 C.4S2+S3 D.3S1+4S3
二、勾股树
1.如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为9cm，则正方形A，B，C，D的面积之和为________cm2.
如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，正方形A，B，C的面积分别是8cm2， 10cm2，14cm2，则正方形D的面积是 cm2．
3．如图，正方形ABDE、CDFI、EFGH的面积分别为25、9、16，△AEH、△BDC、△GFI的面积分别为S1、S2、S3，则S1+S2+S3=
4.（2021·金华）如图，在中，，以该三角形的三条边为边向形外作正方形，正方形的顶点都在同一个圆上．记该圆面积为，面积为，则的值是（ ）
B．C．D．
5.（2020•温州）如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，过点C作CR⊥FG于点R，再过点C作PQ⊥CR分别交边DE，BH于点P，Q．若QH＝2PE，PQ＝15，则CR的长为（ ）
A．14B．15C．83D．65
6.勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为( )
A．90B．100C．110D．121
7.（2019宁波）.勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载.如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，若知道图中阴影的面积，则一定能求出
A.直角三角形的面积 B.最大正方形的面积
C.较小两个正方形重叠部分的面积 D.最大正方形和直角三角形的面积和
勾股数
所谓的勾股数就是使等式 成立的任何三个正整数.我国清代数学家罗士林钻研出一种求勾股数的方法，对于任意正整数m，n(m＞n)，取a＝ ，b＝2mn，c＝ ，则a，b，c就是一组勾股数.请你结合这种方法，写出85(三个数中最大)，84和________组成一组勾股数.
观察下列勾股数组：①3，4，5； ②5，12，13； ③7，24，25；④9，40，41；…．若a，144，145是其中的一组勾股数，则根据你发现的规律，a= ．（提示：5= ，13= ，…）
已知三角形的三边长为n、n＋1、 m (其中m2＝2n＋1)，则此三角形( )．
(A)一定是等边三角形(B)一定是等腰三角形
(C)一定是直角三角形(D)形状无法确定
直角三角形的三边为a﹣b，a，a+b且a、b都为正整数，则三角形其中一边长可能为（ ）
A．61 B．71 C．81 D．91
若a,b,c是直角三角形的三条边长，斜边c上的高的长是h，给出下列结论：
①以a2，b2，c2 的长为边的三条线段能组成一个三角形；
②以a 、b 、c的长为边的三条线段能组成一个三角形；
③以a+b，c+h，h 的长为边的三条线段能组成直角三角形；
④以的长为1a , 1b 、1c 的长为边的三条线段能组成直角三角形，正确结论的序号为 ．