辽宁省沈阳市铁西区2023-2024学年九年级下学期零模数学模拟预测题(无答案)

这是一份辽宁省沈阳市铁西区2023-2024学年九年级下学期零模数学模拟预测题(无答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（本试卷共23道题 满分120分 考试时间120分钟）
第一部分 选择题（共30分）
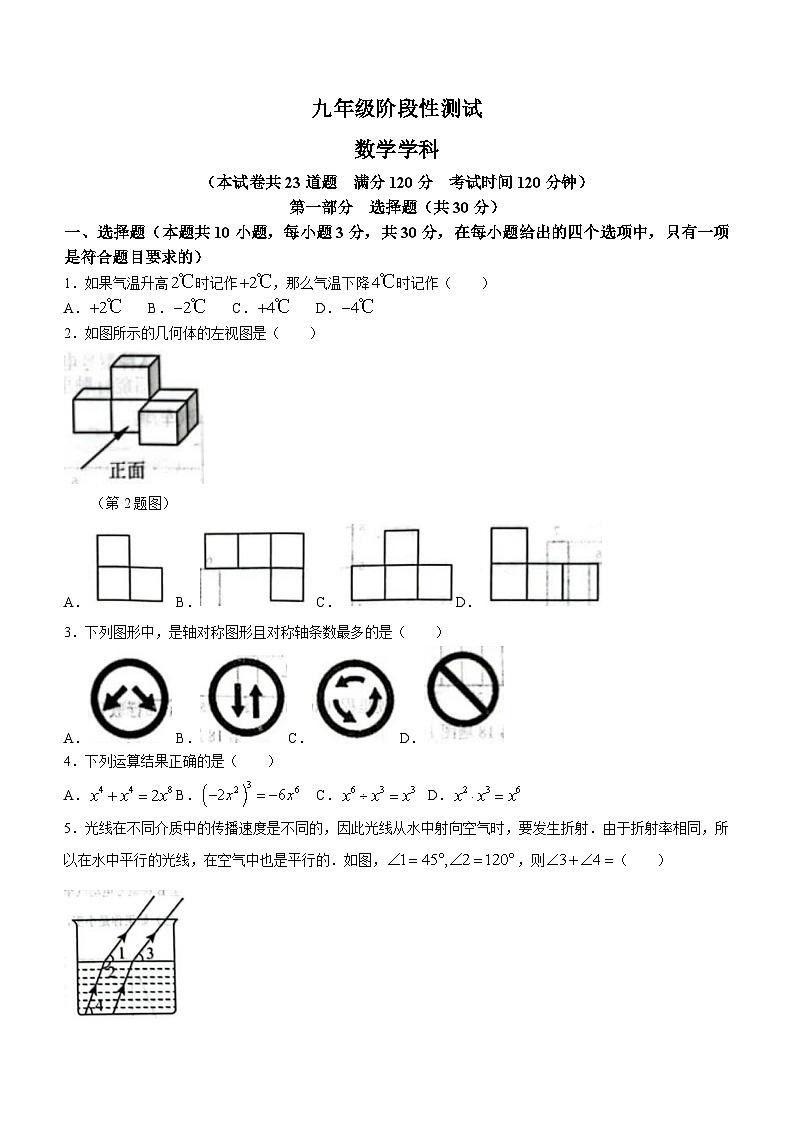
一、选择题（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．如果气温升高时记作，那么气温下降时记作（ ）
A．B．C．D．
2．如图所示的几何体的左视图是（ ）
（第2题图）
A．B．C．D．
3．下列图形中，是轴对称图形且对称轴条数最多的是（ ）
A．B．C．D．
4．下列运算结果正确的是（ ）
A．B．C．D．
5．光线在不同介质中的传播速度是不同的，因此光线从水中射向空气时，要发生折射．由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，，则（ ）
（第5题图）
A．B．C．D．
6．计算的结果是（ ）
A．3B．C．1D．
7．若一次函数的函数值随的增大而减小，则值可能是（ ）
A．2B．C．D．
8．小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店这三天揽件日平均增长率为，根据题意，下面所列方程正确的是（ ）
A．B．
C．D．
9．如图，在等腰中，，分别以点，点为圆心，大于为半径画弧，两弧分别交于点和点，连接，直线与交于点，连接，则的度数是（ ）
（第9题图）
A．B．C．D．
10．如图1，在Rt中，动点从点运动到点再到点后停止，速度为2个单位/s，其中的长与运动时间的关系如图2所示，则边的长为（ ）
（第10题图1） （第10题图2）
A．B．C．17D．
第二部分 非选择题（共90分）
二、填空题（本题共5小题，每小题3分，共15分）
11．若为两个连续整数，且，则______．
12．如图，点为正方形网格中的3个格点，则______．
（第12题图）
13．一个不透明布袋里装有6个红球和个白球（仅有颜色不同）．若从中任意摸出一个球是红球的概率为，则______．
14．如图，在平面直角坐标系中，矩形的顶点和正方形的顶点都在反比例函数的图象上，点在轴上，点在轴上，点的坐标为，则点的坐标为______．
（第14题图）
15．如图，在矩形中，，点是边的中点，连接交于点的平分线交边于点，点关于过点的某条直线的对称点恰好在上，且点不与点重合，连接，则的长为______．
（第15题图）
三、解答题（本题共8小题，共75分．解答题应写出文字说明、演算步骤或推理过程）
16．计算（每题5分，共10分）
（1）；（2）．
17．（本小题8分）
某工厂计划下个月生产甲，乙两种产品共900件，甲、乙两种产品的相关信息如下表：
（成品率每月生产产品合格可销售的件数每月生产产品总的件数）
若该工厂下个月生产甲种产品件，销售甲、乙两种产品的总利润为元，
（1）求与之间的函数关系式（不必写自变量的取值范围）；
（2）若该工厂下个月计划生产的甲、乙两种产品的总成品率不低于，且销售利润最大，求此时的最大利润是多少元？
18．（本小题9分）
小王计划下周日租一辆电动汽车去海边游玩一天，往返行程为．他到某租车公司了解到，该公司有若干辆两种型号电动汽车出租，两种型号每辆车每天费用分别为400元，500元．为了选择合适的型号，小王通过调查，了解到该公司这两种型号电动汽车各有20辆，每辆电动汽车充满电后行驶里程的部分数据，如下面的表格和统计图所示．
种型号电动汽车充满电后能行驶里程条形统计图
（第18题图1）
种型号电动汽车充满电后能行驶里程条形统计图
（第18题图2）
（1）表格中，的值为______，的值为______；
（2）已知种型号电动汽车充满电后能行驶里程可分成如图2所示的五种情况，请直接补全种型号电动汽车充满电后能行驶里程条形统计图；
（3）如果你是小王，你会选择用哪种型号的电动汽车？请说明理由．
19．（本小题8分）
甲、乙两地相距200千米，货车从甲地出发，行驶1小时后在途中的丙地出现故障，技术人员乘轿车以100千米/小时的速度从甲地赶来维修（沟通时间忽略不计）．到达丙地修好车后以原速原路返回，同时货车改变速度前往乙地．两车距乙地的路程（千米）与货车驶时间（小时）之间的函数关系如图所示，请结合图象回答下列问题．
（第19题图）
（1）求货车出现故障前的速度；
（2）求点的坐标；
（3）货车修好后，货车与轿车相距40千米时，求的值．
20．（本小题8分）
某零件的剖面示意图如图所示，，点在线段上，且四边形是正方形，，垂足为点，求的长．（结果精确到，参考数据：，）
（第20题图）
21．（本小题8分）
如图，点在的直径的延长线上，是的切线，点是切点，于点交于点，且．
（第21题图）
（1）求的长；
（2）求的长．
22．（本小题12分）
【基础应用】
（1）如图1，在平面直角坐标系中，点的坐标为，点的坐标为，点的坐标为，点在第一象限，且轴，求点的坐标；
【变式应用一】
（2）如图2，在平面直角坐标系中，点在函数的图象上，点在第二象限，连接，点恰好在反比例函数的图象上，则的值为______；
【变式应用二】
（3）如图3，在平面直角坐标系中，二次函数的图象与轴交于点和点，点在点的右侧，点在轴的正半轴上，连接，在第一象限作矩形，点在二次函数的图象的对称轴上，连接，若，求点的坐标．
（第22题图1） （第22题图2） （第22题图3）
23．（本小题12分）
【方法归纳】
（1）在中，点在边上，交于点，将绕点逆时针旋转，得到，其中点的对应点是点，点的对应点是点，连接，．
①如图1，如果，求的值；
②如图2，如果的延长线与线段交于点，求的度数；
【方法应用】
（2）如图3，在四边形中，，连接，且，则四边形的对角线的长度最大值为______．
（第23题图1） （第23题图2） （第23题图3）
产品
每件利润（元/件）
成品率
甲
100
乙
80
型号
平均里程
中位数
众数
215
227.5
227.5