重难点突破01 玩转外接球、内切球、棱切球（二十三大题型）-2024年高考数学一轮复习（新教材新高考）

这是一份重难点突破01 玩转外接球、内切球、棱切球（二十三大题型）-2024年高考数学一轮复习（新教材新高考），文件包含重难点突破01玩转外接球内切球棱切球二十三大题型原卷版docx、重难点突破01玩转外接球内切球棱切球二十三大题型解析版docx等2份试卷配套教学资源，其中试卷共156页， 欢迎下载使用。
2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。
4、重视错题。错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
重难点突破01 玩转外接球、内切球、棱切球
目录
知识点一：正方体、长方体外接球
1、正方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．
2、长方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．
3、补成长方体
（1）若三棱锥的三条侧棱两两互相垂直，则可将其放入某个长方体内，如图1所示．
（2）若三棱锥的四个面均是直角三角形，则此时可构造长方体，如图2所示．
（3）正四面体可以补形为正方体且正方体的棱长，如图3所示．
（4）若三棱锥的对棱两两相等，则可将其放入某个长方体内，如图4所示
图1 图2 图3 图4
知识点二：正四面体外接球
如图，设正四面体的的棱长为，将其放入正方体中，则正方体的棱长为，显然正四面体和正方体有相同的外接球．正方体外接球半径为，即正四面体外接球半径为．
知识点三：对棱相等的三棱锥外接球
四面体中，，，，这种四面体叫做对棱相等四面体，可以通过构造长方体来解决这类问题．
如图，设长方体的长、宽、高分别为，则，三式相加可得而显然四面体和长方体有相同的外接球，设外接球半径为，则，所以．
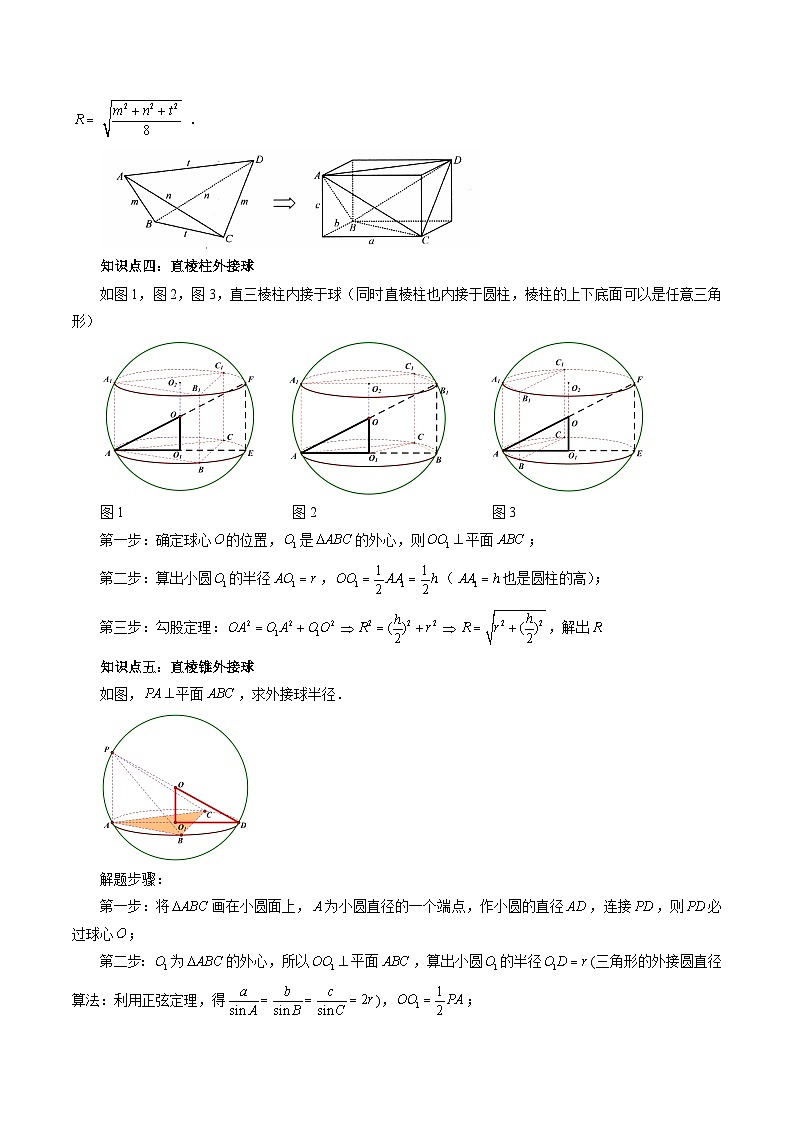
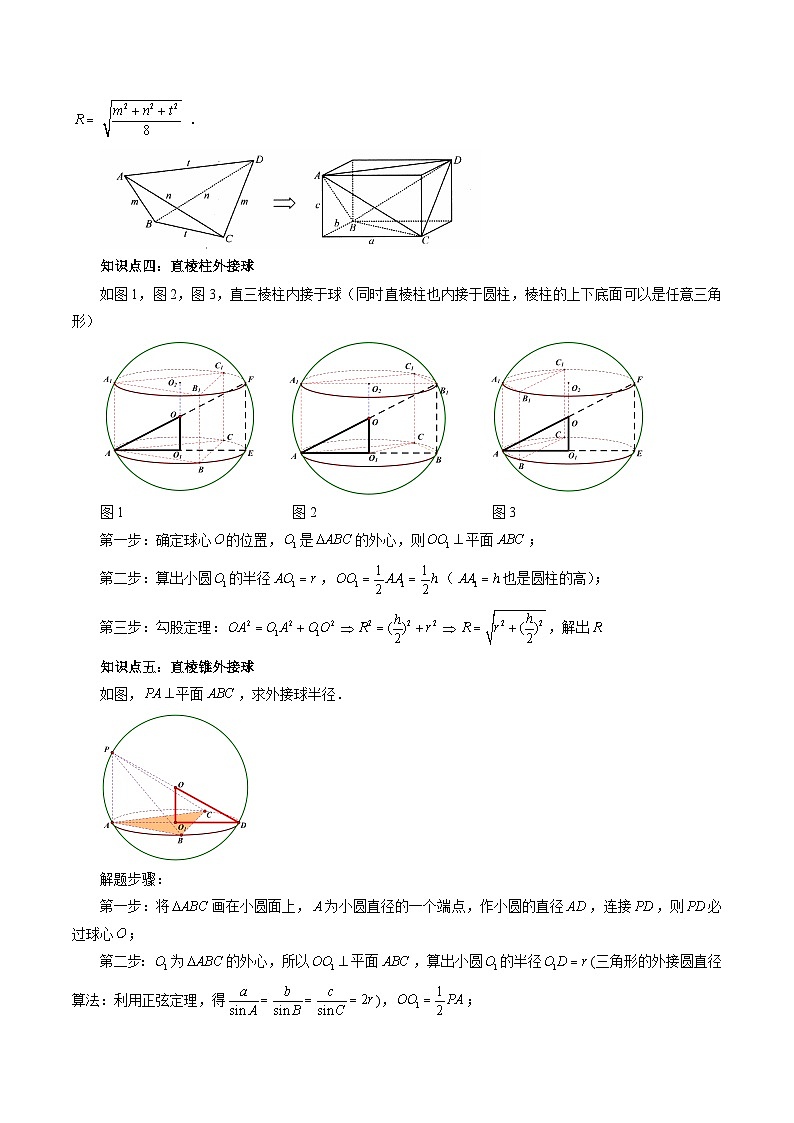
知识点四：直棱柱外接球
如图1，图2，图3，直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）

图1 图2 图3
第一步：确定球心的位置，是的外心，则平面；
第二步：算出小圆的半径，（也是圆柱的高）；
第三步：勾股定理：，解出
知识点五：直棱锥外接球
如图，平面，求外接球半径．
解题步骤：
第一步：将画在小圆面上，为小圆直径的一个端点，作小圆的直径，连接，则必过球心；
第二步：为的外心，所以平面，算出小圆的半径(三角形的外接圆直径算法：利用正弦定理，得)，；
第三步：利用勾股定理求三棱锥的外接球半径： = 1 \* GB3 ①；
= 2 \* GB3 ②．
知识点六：正棱锥与侧棱相等模型
1、正棱锥外接球半径： ．
2、侧棱相等模型：
如图，的射影是的外心
三棱锥的三条侧棱相等
三棱锥的底面在圆锥的底上，顶点点也是圆锥的顶点．

解题步骤：
第一步：确定球心的位置，取的外心，则三点共线；
第二步：先算出小圆的半径，再算出棱锥的高（也是圆锥的高）；
第三步：勾股定理：，解出．
知识点七：侧棱为外接球直径模型
方法：找球心，然后作底面的垂线，构造直角三角形．
知识点八：共斜边拼接模型
如图，在四面体中，，，此四面体可以看成是由两个共斜边的直角三角形拼接而形成的，为公共的斜边，故以“共斜边拼接模型”命名之．设点为公共斜边的中点，根据直角三角形斜边中线等于斜边的一半的结论可知，，即点到，，，四点的距离相等，故点就是四面体外接球的球心，公共的斜边就是外接球的一条直径．
知识点九：垂面模型
如图1所示为四面体，已知平面平面，其外接球问题的步骤如下：
（1）找出和的外接圆圆心，分别记为和．
（2）分别过和作平面和平面的垂线，其交点为球心，记为．
（3）过作的垂线，垂足记为，连接，则．
（4）在四棱锥中，垂直于平面，如图2所示，底面四边形的四个顶点共圆且为该圆的直径．

图1 图2
知识点十：最值模型
这类问题是综合性问题，方法较多，常见方法有：导数法，基本不等式法，观察法等
知识点十一：二面角模型
如图1所示为四面体，已知二面角大小为，其外接球问题的步骤如下：
（1）找出和的外接圆圆心，分别记为和．
（2）分别过和作平面和平面的垂线，其交点为球心，记为．
（3）过作的垂线，垂足记为，连接，则．
（4）在四棱锥中，垂直于平面，如图2所示，底面四边形的四个顶点共圆且为该圆的直径．

知识点十二：坐标法
对于一般多面体的外接球，可以建立空间直角坐标系，设球心坐标为，利用球心到各顶点的距离相等建立方程组，解出球心坐标，从而得到球的半径长．坐标的引入，使外接球问题的求解从繁琐的定理推论中解脱出来，转化为向量的计算，大大降低了解题的难度．
知识点十三：圆锥圆柱圆台模型
1、球内接圆锥
如图，设圆锥的高为，底面圆半径为，球的半径为．通常在中，由勾股定理建立方程来计算．如图，当时，球心在圆锥内部；如图，当时，球心在圆锥外部．和本专题前面的内接正四棱锥问题情形相同，图2和图3两种情况建立的方程是一样的，故无需提前判断．
由图、图可知，或，故，所以．
2、球内接圆柱
如图，圆柱的底面圆半径为，高为，其外接球的半径为，三者之间满足．
3、球内接圆台
，其中分别为圆台的上底面、下底面、高．
知识点十四：锥体内切球
方法：等体积法，即
知识点十五：棱切球
方法：找切点，找球心，构造直角三角形
题型一：外接球之正方体、长方体模型
例1．（2023·云南昆明·高一校考期末）正方体的表面积为96，则正方体外接球的表面积为
例2．（2023·吉林·高一校联考期末）已知正方体的顶点都在球面上，若正方体棱长为，则球的表面积为 ．
例3．（2023·全国·高一专题练习）已知长方体的顶点都在球表面上，长方体中从一个顶点出发的三条棱长分别为2，3，4则球的表面积是
变式1．（2023·湖南长沙·高一长郡中学校考期中）长方体的外接球的表面积为，，，则长方体的体积为 .
变式2．（2023·天津静海·高一校考期中）在长方体中，，，，则长方体外接球的表面积为 ．
题型二：外接球之正四面体模型
例4．（2023·湖北宜昌·宜昌市夷陵中学校考模拟预测）已知正四面体ABCD的表面积为，且A，B，C，D四点都在球O的球面上，则球O的体积为 ．
例5．（2023·浙江·高二校联考期中）正四面体的所有顶点都在同一个表面积是36π的球面上，则该正四面体的棱长是 ．
例6．（2023·全国·高三专题练习）棱长为的正四面体的外接球体积为 .
变式3．（2023·全国·高一假期作业）正四面体和边长为1的正方体有公共顶点，，则该正四面体的外接球的体积为 .
变式4．（2023·安徽池州·高二池州市第一中学校考期中）正四面体中，其侧面积与底面积之差为，则该正四面体外接球的体积为 .
题型三：外接球之对棱相等的三棱锥模型
例7．（2023·高一单元测试）在四面体中，若，，，则四面体的外接球的表面积为（ ）
A．B．C．D．
例8．（2023·河南·开封高中校考模拟预测）已知四面体ABCD中，，，，则四面体ABCD外接球的体积为（ ）
A．B．C．D．
例9．（2023·广东揭阳·高二校联考期中）在三棱锥中，，，，则该三棱锥的外接球表面积是（ ）
A．B．C．D．
变式5．（2023·全国·高三专题练习）如图，在三棱锥中，，，，则三棱锥外接球的体积为（ ）
A．B．C．D．
题型四：外接球之直棱柱模型
例10．（2023·陕西安康·统考三模）已知矩形ABCD的周长为36，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为 ．
例11．（2023·黑龙江齐齐哈尔·高一齐齐哈尔市第八中学校校考阶段练习）设直三棱柱的所有顶点都在一个表面积是的球面上，且，则此直三棱柱的表面积是（ ）
A．B．C．D．
例12．（2023·全国·高三专题练习）在直三棱柱中，为等腰直角三角形，若三棱柱的体积为32，则该三棱柱外接球表面积的最小值为（ ）
A．12πB．24πC．48πD．96π
变式6．（2023·湖北咸宁·高二鄂南高中校考阶段练习）已知正三棱柱的体积为，则其外接球表面积的最小值为（ ）
A．12πB．6πC．16πD．8π
变式7．（2023·全国·高三专题练习）在三棱柱中，已知，侧面，且直线与底面所成角的正弦值为,则此三棱柱的外接球的表面积为（ ）
A．B．C．D．
变式8．（2023·新疆昌吉·高三校考期末）已知正三棱柱所有棱长都为6，则此三棱柱外接球的表面积为（ ）
A．B．60C．D．
题型五：外接球之直棱锥模型
例13．（2023·安徽宣城·高一统考期末）在三棱锥中，△ABC是边长为3的等边三角形，侧棱PA⊥平面ABC，且，则三棱锥的外接球表面积为 ．
例14．（2023·江苏南京·高二统考期末）在三棱锥中，面，为等边三角形，且，则三棱锥的外接球的表面积为 ．
例15．（2023·四川成都·高一成都七中校考阶段练习）已知三棱锥，其中平面，则三棱锥外接球的表面积为 .
变式9．（2023·陕西商洛·镇安中学校考模拟预测）在三棱锥中，为等边三角形，平面，若，则三棱锥外接球的表面积的最小值为 .
变式10．（2023·陕西榆林·高二校考阶段练习）已知三棱锥中，平面，，异面直线与所成角的余弦值为，则三棱锥的外接球的表面积为 ．
变式11．（2023·江苏镇江·高三江苏省镇江中学校考阶段练习）如图，在四棱锥中，底面为菱形，底面，为对角线与的交点，若，，则三棱锥的外接球的体积为 .
变式12．（2023·四川绵阳·绵阳中学校考二模）在四棱锥中，平面BCDE，，，，且，则该四棱锥的外接球的表面积为 .
变式13．（2023·广东韶关·高二统考期末）三棱锥中,平面,,,,则三棱锥外接球的体积是 ．
题型六：外接球之正棱锥、正棱台模型
例16．（2023·山东滨州·高一校考期中）已知正四棱锥的底面边长为，侧棱长为6，则该四棱锥的外接球的体积为 ．
例17．（2023·福建福州·高一福建省福州屏东中学校考期末）已知正三棱锥的顶点都在球O的球面上，其侧棱与底面所成角为，且，则球O的表面积为
例18．（2023·河南商丘·高一商丘市第一高级中学校联考期末）在正三棱锥中，点D在棱上，且满足，，若，则三棱锥外接球的表面积为 .
变式14．（2023·云南保山·高一统考期末）已知正三棱锥的侧棱与底面所成的角为，高为，则该三棱锥外接球的表面积为 .
变式15．（2023·广东佛山·高一佛山市南海区第一中学校考阶段练习）已知正三棱锥中，，，该三棱锥的外接球体积为 ．
变式16．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）如图，在正三棱台中，，，，则正三棱台的外接球表面积为（ ）

A．64B．C．D．
变式17．（2023·辽宁·高三校联考期末）正四棱台高为2，上下底边长分别为2和4，所有顶点在同一球面上，则球的表面积为（ ）
A．B．C．D．
变式18．（2023·贵州六盘水·高一校考阶段练习）已知正四棱锥的底面边长为6，侧棱长为，则该四棱锥外接球的表面积为 ．
变式19．（2023·山西晋中·高三祁县中学校考阶段练习）在正四棱锥中，，若四棱锥的体积为，则该四棱锥外接球的体积为 ．
变式20．（2023·湖北·高三统考阶段练习）在正四棱台中，，．当该正四棱台的体积最大时，其外接球的表面积为（ ）
A．B．C．D．
题型七：外接球之侧棱相等的棱锥模型
例19．（2023·安徽安庆·校联考模拟预测）三棱锥中，，，，则该三棱锥外接球的表面积为 ．
例20．（2023·江苏常州·高三华罗庚中学校考阶段练习）在三棱锥中，，二面角的大小为，则三棱锥的外接球的表面积为 ．
例21．（2023·河北承德·高一校联考阶段练习）已知三棱锥的各侧棱长均为，且，则三棱锥的外接球的表面积为 .
变式21．（2023·吉林长春·高一长春市解放大路学校校考期末）已知三棱锥P-ABC的四个顶点在球O的球面上，，△ABC是边长为的正三角形，E，F分别是PA，AB的中点，，则球O的体积为 .
变式22．（2023·全国·高三专题练习）已知在三棱锥中，，，则该三棱锥外接球的体积为
A．B．C．D．
变式23．（2023·全国·高一专题练习）如图，在三棱锥中，，，二面角的大小为，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
变式24．（2023·全国·高三专题练习）在四面体中，，，则四面体的外接球的表面积为（ ）
A．B．C．sD．
题型八：外接球之圆锥、圆柱、圆台模型
例22．（2023·浙江台州·高二校联考期末）已知圆锥的底面半径为1，母线长为2，则该圆锥的外接球的体积为 .
例23．（2023·黑龙江哈尔滨·哈尔滨三中校考模拟预测）已知某圆锥的轴截面为正三角形，侧面积为，该圆锥内接于球，则球的表面积为 .
例24．（2023·河北石家庄·高二校考阶段练习）一个圆柱的底面直径与高都等于一个球的直径，则圆柱的表面积与球的表面积之比为 .
变式25．（2023·重庆·统考模拟预测）如图所示，已知一个球内接圆台，圆台上、下底面的半径分别为和，球的体积为，则该圆台的侧面积为（ ）

A．B．C．D．
变式26．（2023·云南·高三校联考开学考试）已知圆台的上下底面圆的半径分别为3，4，母线长为，若该圆台的上下底面圆的圆周均在球O的球面上，则球O的体积为（ ）
A．B．C．D．
变式27．（2023·陕西西安·高一校考期中）如图所示，一个球内接圆台，已知圆台上､下底面的半径分别为3和4，球的表面积为，则该圆台的体积为（ ）
A．B．C．D．
题型九：外接球之垂面模型
例25．（2023·江西九江·高一校考期末）如图，三棱锥中，平面平面BCD，是边长为2的等边三角形，，.若A，B，C，D四点在某个球面上，则该球体的表面积为 .

例26．（2023·四川乐山·高二期末）已知正边长为1，将绕旋转至，使得平面平面，则三棱锥的外接球表面积为 ．
例27．（2023·河南平顶山·高一统考期末）在三棱锥中，平面平面，点是的中点，，则三棱锥的外接球的表面积为 .
变式28．（2023·江苏·高一专题练习）如图，在直三棱柱中，．设D为的中点，三棱锥的体积为，平面平面，则三棱柱外接球的表面积为 ．
变式29．（2023·河南开封·开封高中校考模拟预测）如图,在三棱锥中,平面平面ABC,,,,为等边三角形,则三棱锥外接球的表面积为 ．
变式30．（2023·湖北十堰·高一统考期末）如图，在平面四边形中，，沿对角线将折起，使平面平面，连接，得到三棱锥，则三棱锥外接球表面积的最小值为 .

变式31．（2023·河南安阳·高一统考期末）在三棱锥中，平面平面，，且，是等边三角形，则该三棱锥外接球的表面积为 ．
变式32．（2023·云南临沧·高二校考期中）如图，已知矩形中，，现沿折起，使得平面平面，连接，得到三棱锥，则其外接球的体积为 ．

变式33．（2023·全国·高三校联考开学考试）在三棱锥中，平面平面，底面是边长为3的正三角形，若该三棱锥外接球的表面积为，则该三棱锥体积的最大值为 .
变式34．（2023·四川乐山·统考三模）在三棱锥中，，平面平面ABC，则三棱锥的外接球表面积的最小值为 ．
变式35．（2023·湖南衡阳·校联考模拟预测）在平面四边形中，，沿对角线将折起，使平面平面，得到三棱锥，则三棱锥外接球表面积的最小值为 .
题型十：外接球之二面角模型
例28．（2023·广东阳江·高三统考开学考试）在三棱锥中，，，二面角的平面角为，则三棱锥外接球表面积的最小值为（ ）
A．B．
C．D．
例29．（2023·浙江丽水·高二统考期末）在四面体PABC中，，是边长为2的等边三角形，若二面角的大小为，则四面体的外接球的表面积为（ ）
A．B．C．D．
例30．（2023·广东·校联考模拟预测）已知四棱锥平面，二面角的大小为.若点均在球的表面上，则该球的表面积为（ ）
A．B．C．D．
变式36．（2023·福建·高一福建师大附中校考期末）在四面体中，与都是边长为6的等边三角形，且二面角的大小为，则四面体外接球的表面积是（ ）
A．52πB．54πC．56πD．60π
变式37．（2023·甘肃张掖·高台县第一中学校考模拟预测）图1为两块大小不同的等腰直角三角形纸板组成的平面四边形ABCD，其中小三角形纸板的斜边AC与大三角形纸板的一条直角边长度相等，小三角形纸板的直角边长为a，现将小三角形纸板ACD沿着AC边折起，使得点D到达点M的位置，得到三棱锥，如图2．若二面角的大小为，则所得三棱锥M－ABC的外接球的表面积为（ ）

A．B．C．D．
变式38．（2023·全国·高三专题练习）如图1，在中，，，，，沿将折起，使得二面角为60°，得到三棱锥，如图2，若，则三棱锥的外接球的表面积为（ ）

A．B．C．D．
变式39．（2023·湖南岳阳·统考三模）已知三棱锥的所有顶点都在球的球面上，，二面角的大小为，若球的表面积等于，则三棱锥的体积等于（ ）
A．B．
C．D．
变式40．（2023·全国·高一专题练习）在三棱锥中，，二面角为，则三棱锥外接球的表面积为（ ）
A．B．C．D．
题型十一：外接球之侧棱为球的直径模型
例31．（2023·贵州黔东南·高二凯里一中校考期中）已知三棱锥的所有顶点都在球的球面上，是球的直径.若平面平面，，，三棱锥的体积为，则球的体积为（ ）
A．B．C．D．
例32．（2023·四川巴中·高三统考期末）已知三棱锥的体积为，，，若是其外接球的直径，则球的表面积为（ ）
A．B．C．D．
例33．（2023·重庆九龙坡·高二重庆市育才中学校考期中）已知三棱锥的所有顶点都在球的球面上,为球的直径,是边长为的等边三角形,三棱锥的体积为,则球的表面积为( )
A．B．C．D．
变式41．（2023·重庆·校联考一模）已知三棱锥各顶点均在球上，为球的直径，若，，三棱锥的体积为4，则球的表面积为
A．B．C．D．
变式42．（2023·河北唐山·统考三模）三棱锥的四个顶点都在球面上，是球的直径，，，则该球的表面积为
A．B．C．D．
变式43．（2023·河南南阳·统考模拟预测）已知三棱锥的所有顶点都在球的球面上，是球的直径.若平面平面，，，三棱锥的体积为，则球的体积为
A．B．C．D．
变式44．（2023·福建莆田·高三统考期中）三棱锥的各顶点均在球上，为该球的直径，，三棱锥的体积为，则球的表面积为
A．B．C．D．
变式45．（2023·全国·高三专题练习）已知三棱锥的四个顶点均在某球面上，为该球的直径，是边长为4的等边三角形，三棱锥的体积为，则该三棱锥的外接球的表面积为（ ）
A．B．C．D．
变式46．（2023·湖南长沙·高三长郡中学校考阶段练习）已知是球的直径，是球球面上的两点，且，若三棱锥的体积为，则球的表面积为
A．B．C．D．
题型十二：外接球之共斜边拼接模型
例34．（2022·江西·高二阶段练习（理））如图，在四棱锥P-ABCD中，底面是菱形， 底面ABCD， 是对角线与的交点，若，，则三棱锥的外接球的体积为（ ）
A．B．C．D．
例35．（2022·安徽·芜湖一中高二期中）已知三棱锥中，，，，，，则此三棱锥的外接球的表面积为（ ）
A．B．C．D．
例36．（2022·江西赣州·高二期中（理））在三棱锥中，若该三棱锥的体积为，则三棱锥外球的体积为（ ）
A．B．C．D．
变式47．在矩形中，，沿将矩形折成一个直二面角，则四面体的外接球的体积为（ ）
A． B． C． D．
变式48．三棱锥中，平面平面， ，，，则三棱锥的外接球的半径为
题型十三：外接球之坐标法模型
例37．（2023·浙江·高二校联考阶段练习）空间直角坐标系中，则四面体ABCD外接球体积是（ ）
A．B．C．D．
例38．（2023·贵州·统考模拟预测）如图，某环保组织设计一款苗木培植箱，其外形由棱长为2（单位：）的正方体截去四个相同的三棱锥（截面为等腰三角形）后得到.若将该培植箱置于一球形环境中，则该球表面积的最小值为
例39．（2023·河南开封·开封高中校考一模）如图，在三棱锥中，为等边三角形，三棱锥的体积为，则三棱锥外接球的表面积为 .
变式49．（2023·全国·高三专题练习）如图①，在中，，，D，E分别为，的中点，将沿折起到的位置，使，如图②.若F是的中点，则四面体的外接球体积是（ ）
A．B．C．D．
变式50．（2023·湖北武汉·高一武汉外国语学校（武汉实验外国语学校）期末）如图，已知四棱锥，底面是边长为3的正方形，面，，，，若，则四棱锥外接球表面积为（ ）

A．B．C．D．
变式51．（2023·河南郑州·模拟预测）在长方体中中，，AD＝2，M是棱的中点，过点B，M，的平面交棱AD于点N，点P为线段上一动点，则三棱锥外接球表面积的最小值为 ．
变式52．（2023·湖南郴州·高二统考期末）如图，棱长为2的正方体中，E，F分别为棱､的中点，G为面对角线上一个动点，则三棱锥的外接球表面积的最小值为 .
变式53．（2023·广东阳江·高三阳春市第一中学阶段练习）已知正方体的棱长为2，点是线段上的动点，则三棱锥的外接球半径的取值范围为 ．
题型十四：外接球之空间多面体
例40．（2023·全国·高三专题练习）自2015年以来，贵阳市着力建设“千园之城”，构建贴近生活、服务群众的生态公园体系，着力将“城市中的公园”升级为“公园中的城市”．截至目前，贵阳市公园数量累计达到1025个．下图为贵阳市某公园供游人休息的石凳，它可以看做是一个正方体截去八个一样的四面体得到的，如果被截正方体的的棱长为，则石凳所对应几何体的外接球的表面积为 ．
例41．（2023·山东青岛·高一山东省青岛第五十八中学校考阶段练习）截角四面体是一种半正八面体，可由四面体经过适当的截角，即截去四面体的四个顶点所产生的多面体.如图所示，将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体，则该截角四面体的外接球表面积为 .
例42．（2023·宁夏银川·银川二中校考一模）把一个棱长都是6的正四棱锥（底面是正方形，顶点在底面的射影是正方形的中心）每条棱三等分，沿与正四棱锥顶点相邻的三等分点做截面，将正四棱锥截去四个小正四面体和一个小正四棱锥（如图所示），则剩下的几何体的外接球的表面积等于 ．
变式54．（2023·山东济南·高一山东省济南市莱芜第一中学校考阶段练习）取两个相互平行且全等的正n边形，将其中一个旋转一定角度，连接这两个多边形的顶点，使得侧面均为等边三角形，我们把这种多面体称作“n角反棱柱”.当n=4时，得到如图所示棱长均为2的“四角反棱柱”，则该“四角反棱柱”外接球的表面积等于（ ）
A．B．C．D．
题型十五：与球有关的最值问题
例43．（2023·江西抚州·统考模拟预测）如图，直三棱柱中，，棱柱的侧棱足够长，点P在棱上，点在上，且，则当△的面积取最小值时，三棱锥的外接球的体积为 .
例44．（2023·全国·学军中学校联考二模）如图，直三棱柱中，，点在棱上，且，当的面积取最小值时，三棱锥的外接球的表面积为 .
例45．（2023·湖南长沙·高三长沙一中校考阶段练习）正方体的棱长为2，点平面，点是线段的中点，若，则当的面积取得最小值时，三棱锥外接球的体积为 .
变式55．（2023·广东深圳·高三深圳中学校考开学考试）如图，直三棱柱中，⊥，，，点P在棱上，且，当的面积取最小值时，三棱锥的外接球的表面积为 ．
变式56．（2023·黑龙江齐齐哈尔·高一校联考期末）已知三棱锥的四个顶点均在同一个球面上，底面为等腰直角三角形且，若该三棱锥体积的最大值为，则其外接球的表面积为 .
变式57．（2023·四川泸州·高三四川省泸县第一中学校考阶段练习）已知四棱锥S－ABCD中，底面ABCD为正方形，侧面SAB为等边三角形，AB＝3，则当四棱锥的体积取得最大值时，其外接球的表面积为 ．
变式58．（2023·湖南长沙·高三宁乡一中校考阶段练习）在三棱锥中，底面，，，为的中点，若三棱锥的顶点均在球的球面上，是球上一点，且三棱锥体积的最大值是，则球的体积为 .
变式59．（2023·江西南昌·南昌十中校考模拟预测）点，，，在同一个球的球面上，，若四面体体积的最大值为，则这个球的表面积为 .
题型十六：内切球之正方体、正棱柱模型
例46．（2023·广东肇庆·高一校考阶段练习）棱长为2的正方体的内切球的球心为，则球的体积为（ ）
A．B．C．D．
例47．（2023·河北邯郸·高一大名县第一中学校考阶段练习）已知直三棱柱存在内切球，若，则该三棱柱外接球的表面积为（ ）
A．B．C．D．
例48．（2023·山西太原·高一校考阶段练习）已知正方体的内切球(球与正方体的六个面都相切)的体积是，则该正方体的体积为（ ）
A．4B．16C．8D．64
变式60．（2023·全国·高一专题练习）若一个正三棱柱存在外接球与内切球，则它的外接球与内切球体积之比为（ ）
A．B．C．D．
变式61．（2023·辽宁·高二沈阳二中校联考开学考试）在正三棱柱中，D是侧棱上一点，E是侧棱上一点，若线段的最小值是﹐且其内部存在一个内切球（与该棱柱的所有面均相切），则该棱柱的外接球表面积为（ ）
A．B．C．D．
变式62．（2023·全国·高一专题练习）若一个正六棱柱既有外接球又有内切球，则该正六棱柱的外接球和内切球的表面积的比值为（ ）
A．B．C．D．
变式63．（2023·全国·高三专题练习）已知点O到直三棱柱各面的距离都相等，球O是直三棱柱的内切球，若球O的表面积为，的周长为4，则三棱锥的体积为（ ）
A．B．C．D．
题型十七：内切球之正四面体模型
例49．（2023·高一课时练习）边长为的正四面体内切球的体积为（ ）
A．B．C．D．
例50．（2023·全国·高三专题练习）已知正四面体的棱长为，则其内切球的表面积为（ ）
A．B．
C．D．
例51．（2023·江苏·高一专题练习）正四面体的棱长为，则它的内切球与外接球的表面积之比为（ ）
A．B．C．D．
题型十八：内切球之棱锥模型
例52．（2023·安徽·高二马鞍山二中校联考阶段练习）已知矩形中，，沿着对角线将折起，使得点不在平面内，当时，求该四面体的内切球和外接球的表面积比值为（ ）
A．B．C．D．
例53．（2023·广西·高二校联考期中）已知四棱锥的各棱长均为2，则其内切球表面积为（ ）

A．B．
C．D．
例54．（2023·湖北武汉·高二校联考阶段练习）如图，在三棱锥中，，，若三棱锥的内切球的表面积为，则此三棱锥的体积为（ ）
A．B．C．D．
变式64．（2023·河南濮阳·高一濮阳一高校考阶段练习）在三棱锥中，平面，且，若球在三棱锥的内部且与四个面都相切（称球为三棱锥的内切球），则球的表面积为（ ）
A．B．C．D．
变式65．（2023·福建龙岩·统考模拟预测）如图，已知正方体的棱长为2，以其所有面的中心为顶点的多面体为正八面体，则该正八面体的内切球表面积为（ ）
A．B．C．D．
变式66．（2023·浙江宁波·高一慈溪中学校联考期末）在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑.在鳖臑中，平面，，且，则其内切球表面积为（ ）
A．B．C．D．
题型十九：内切球之圆锥、圆台模型
例55．（2023·全国·高三专题练习）在Rt中，.以斜边为旋转轴旋转一周得到一个几何体，则该几何体的内切球的体积为（ ）
A．B．C．D．
例56．（2023·天津·统考二模）已知一个圆锥的高为，底面直径为，其内有一球与该圆锥的侧面和底面都相切，则此球的体积为（ ）
A．B．C．D．
例57．（2023·全国·高一专题练习）已知某圆锥的母线长为2，其轴截面为直角三角形，则下列关于该圆锥的说法中错误的是（ ）
A．圆锥的体积为B．圆锥的表面积为
C．圆锥的侧面展开图是圆心角为的扇形D．圆锥的内切球表面积为
变式67．（2023·贵州贵阳·高二校考阶段练习）已知圆锥内切球（与圆锥侧面、底面均相切的球）的半径为2，当该圆锥的表面积最小时，其外接球的表面积为（ ）
A．B．C．D．
变式68．（2023·全国·高一专题练习）已知圆锥的底面半径为2，高为，则该圆锥的内切球表面积为（ ）
A．B．C．D．
变式69．（2023·安徽宣城·高二校联考开学考试）如图，正四棱台的上､下底面边长分别为分别为，的中点，8个顶点构成的十面体恰有内切球，则该内切球的表面积为（ ）
A．B．C．D．
变式70．（2023·湖北咸宁·高二统考期末）已知球内切于圆台（即球与该圆台的上、下底面以及侧面均相切），且圆台的上、下底面半径，则圆台的体积与球的体积之比为（ ）

A．B．C．2D．
题型二十：棱切球之正方体、正棱柱模型
例58．（2023·山东菏泽·高一山东省鄄城县第一中学校考阶段练习）已知球与一正方体的各条棱相切，同时该正方体内接于球，则球与球的表面积之比为（ ）
A．2：3B．3：2C．D．
例59．（2023·全国·高三专题练习）已知正三棱柱的体积为18，若存在球O与三棱柱的各棱均相切，则球O的表面积为（ ）
A．B．C．D．
例60．（2023·全国·高三专题练习）已知球与棱长为的正方体的各条棱都相切，则球内接圆柱的侧面积的最大值为（ ）
A．B．C．D．
变式71．（吉林省吉林市2023届高三第四次数学（理）调研试题）已知正三棱柱(底面为正三角形且侧棱与底面垂直)，它的底面边长为2，若存在一个球与此正三棱柱的所有棱都相切，则此正三棱柱的侧棱长为 .
变式72．（福建省三明市2023届高三上学期期末质量检测数学试题）已知直三棱柱的侧棱长为，底面为等边三角形.若球O与该三棱柱的各条棱都相切，则球O的体积为 .
变式73．已知正三棱柱，若有一半径为4的球与正三棱柱的各条棱均相切，则正三棱柱的侧棱长为 .
变式74．（广东省茂名市五校联盟2023届高三上学期第二次联考数学试题）已知正三棱柱的高等于1.一个球与该正三棱柱的所有棱都相切，则该球的体积为（ ）
A．B．C．D．
题型二十一：棱切球之正四面体模型
例61．（2023·全国·高一期中）已知某棱长为的正四面体的各条棱都与同一球面相切，则该球与此正四面体的体积之比为（ ）
A．B．C．D．
例62．（2023·陕西西安·高一校联考期中）所有棱长均相等的三棱锥构成一个正四面体，则该正四面体的内切球与外接球的体积之比为（ ）
A．B．C．D．
例63．（2023·江西南昌·高二进贤县第一中学校考期中）球与棱长为的正四面体各条棱都相切，则该球的表面积为（ ）
A．B．C．D．
变式75．（2023·贵州贵阳·校联考模拟预测）已知球的表面积为，若球与正四面体的六条棱均相切，则此四面体的体积为（ ）
A．9B．C．D．
变式76．（2023·全国·高三专题练习）正四面体P-ABC的棱长为4，若球O与正四面体的每一条棱都相切，则球O的表面积为（ ）
A．2πB．8πC．D．12π
题型二十二：棱切球之正棱锥模型
例64．（河南省名校2022-2023学年高二下学期5月联考数学试题）已知棱长均为的多面体由上､下全等的正四棱锥和拼接而成，其中四边形为正方形，如图所示，记该多面体的外接球半径为，该多面体的棱切球（与该多面体的所有棱均相切的球）的半径为，则 ．

例65．（河南省多所名校2022-2023学年高三下学期3月月考文科数学试题）在正三棱锥中，，，若球O与三棱锥的六条棱均相切，则球O的表面积为 ．
例66．（安徽省马鞍山市2023届高三下学期第二次教学质量监测理科数学试题）球被平面截下的一部分叫做球缺，截面叫做球缺的底面，垂直于截面的直径被截下的线段长叫做球缺的高，球缺的体积公式，其中为球的半径，为球缺的高.若一球与一所有棱长为6的正四棱锥的各棱均相切，则该球与该正四棱锥的公共部分的体积为 .
变式77．（2023·全国·高三专题练习）正三棱锥的底面边长为，侧棱长为，若球H与正三棱锥所有的棱都相切，则这个球的表面积为（ ）
A．B．C．D．
变式78．（2023·全国·高三专题练习）在三棱锥中，，，两两垂直，，若球与三棱锥各棱均相切，则该球的表面积为（ ）
A．B．C．D．
变式79．（2023·湖北武汉·高一武汉市第一中学校考阶段练习）与正三棱锥6条棱都相切的球称为正三棱锥的棱切球.若正三棱锥的底面边长为，侧棱长为3，则此正三棱锥的棱切球半径为（ ）
A．B．C．D．
变式80．（2023·江苏·高一专题练习）在正三棱锥中，，若球与三棱锥的六条棱均相切，则球的表面积为（ ）
A．B．
C．D．
题型二十三：多球相切问题
例67．（2023·浙江温州·乐清市知临中学校考二模）如今中国被誉为基建狂魔，可谓是逢山开路，遇水架桥.公路里程､高铁里程双双都是世界第一.建设过程中研制出用于基建的大型龙门吊､平衡盾构机等国之重器更是世界领先.如图是某重器上一零件结构模型，中间最大球为正四面体的内切球，中等球与最大球和正四面体三个面均相切，最小球与中等球和正四面体三个面均相切，已知正四面体棱长为，则模型中九个球的表面积和为（ ）
A．B．C．D．
例68．（2023·江西赣州·高一江西省龙南中学校考期末）已知正四面体的棱长为12，先在正四面体内放入一个内切球，然后再放入一个球，使得球与球及正四面体的三个侧面都相切，则球的体积为（ ）
A．B．C．D．
例69．（2023·山东德州·高一德州市第一中学校考期末）如图是某零件结构模型，中间大球为正四面体的内切球，小球与大球和正四面体三个面均相切，若，则该模型中一个小球的体积为（ ）

A．B．C．D．
变式81．（2023·全国·高三专题练习）如图，在一个底面边长为2，侧棱长为的正四棱锥中，大球内切于该四棱锥，小球与大球及四棱锥的四个侧面相切，则小球的表面积为 ．
变式82．（2023·全国·高一专题练习）棱长为的正四面体内切一球，然后在正四面体和该球形成的空隙处各放入一个小球，则这样一个小球的表面积最大为（ ）
A．B．C．D．
变式83．（2023·全国·高三专题练习）已知球是棱长为24的正四面体的内切球，球与球外切且与正四面体的三个侧面都相切，则球的表面积为（ ）
A．B．C．D．
变式84．（2023·全国·高一专题练习）四个半径为2的球刚好装进一个正四面体容器内，此时正四面体各面与球相切，则这个正四面体外接球的表面积为（ ）
A．B．
C．D．