




重难点突破05 立体几何中的常考压轴小题(七大题型)-2024年高考数学一轮复习(新教材新高考)
展开2、精练习题。复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。
3、加强审题的规范性。每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。
4、重视错题。错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
重难点突破05 立体几何中的常考压轴小题
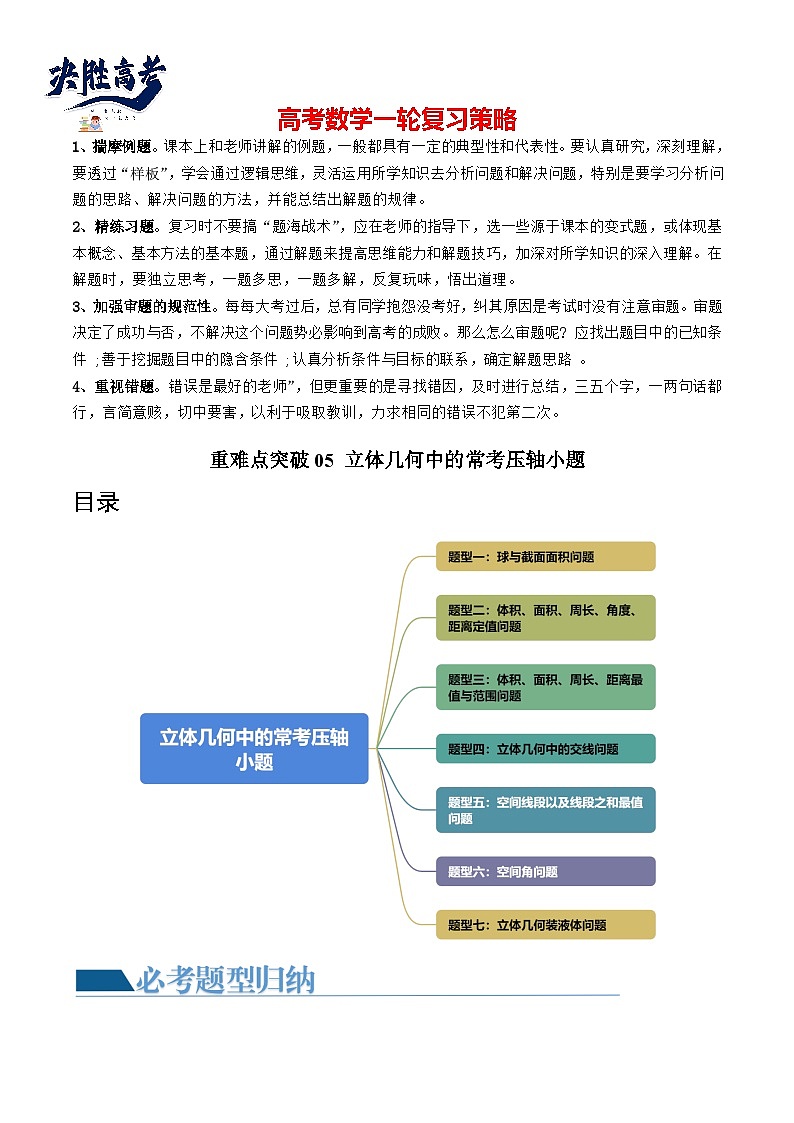
目录
题型一:球与截面面积问题
例1.(2023·湖南长沙·高二长郡中学校考开学考试)已知三棱锥的四个顶点在球O的球面上,,是边长为的正三角形,,,,过点E作球O的截面,截面面积最小值为( )
A.B.C.D.
例2.(2023·四川绵阳·高三绵阳南山中学实验学校校考阶段练习)四面体ABCD的四个顶点都在球的球面上,,,点E,F,G分别为棱BC,CD,AD的中点,现有如下结论:①过点E,F,G作四面体ABCD的截面,则该截面的面积为2;②四面体ABCD的体积为;③过作球的截面,则截面面积的最大值与最小值的比为5:4.则上述说法正确的个数是( )
A.0B.1C.2D.3
例3.(2023·四川内江·四川省内江市第六中学校考模拟预测)已知球是正三棱锥(底面是正三角形,顶点在底面的射影为底面中心)的外接球,,,点是线段的中点,过点作球的截面,则所得截面面积的最小值是( )
A.B.C.D.
变式1.(2023·宁夏银川·校联考二模)2022年第三十二届足球世界杯在卡塔尔举行,第一届世界杯是1930年举办的,而早在战国中期,中国就有过类似的体育运动项目:蹴鞠,又名蹴球,蹴圆,筑球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似于今日的足球.2006年5月20日,蹴鞠作为非物质文化遗产经国务院批准已列入第一批国家非物质文化遗产名录.已知半径为的某鞠(球)的表面上有四个点,,,,,,,则该鞠(球)被平面所截的截面圆面积为( )
A.B.C.D.
变式2.(2023·全国·高三专题练习)在正方体中,分别为的中点,该正方体的外接球为球,则平面截球得到的截面圆的面积为( )
A.B.C.D.
变式3.(2023·四川遂宁·射洪中学校考模拟预测)已知球O内切于正方体,P,Q,M,N分别是的中点,则该正方体及其内切球被平面所截得的截面面积之比为( )
A.B.C.D.
变式4.(2023·河南洛阳·高三校联考阶段练习)已知三棱锥P-ABC的棱长均为6,且四个顶点均在球心为O的球面上,点E在AB上,,过点E作球O的截面,则截面面积的最小值为( )
A.B.C.D.
题型二:体积、面积、周长、角度、距离定值问题
例4.(2023·福建三明·高一校考阶段练习)如图,在正方体中,,,分别为,的中点,,分别为棱,上的动点,则三棱锥的体积( )
A.存在最大值,最大值为B.存在最小值,最小值为
C.为定值D.不确定,与,的位置有关
例5.(2023·四川成都·校考模拟预测)如图,在四棱柱中,底面为正方形,底面,,、分别是棱、上的动点,且,则下列结论中正确的是( )
A.直线与直线可能异面
B.三棱锥的体积保持不变
C.直线与直线所成角的大小与点的位置有关
D.直线与直线所成角的最大值为
例6.(多选题)(2023·福建三明·统考三模)如图,正方体的棱长为,点是的中点,点是侧面内一动点,则下列结论正确的为( )
A.当在上时,三棱锥的体积为定值
B.与所成角正弦的最小值为
C.过作垂直于的平面截正方体所得截面图形的周长为
D.当时,面积的最小值为
变式5.(多选题)(2023·广东梅州·统考三模)已知正方体的棱长为2,为四边形的中心,为线段上的一个动点,为线段上一点,若三棱锥的体积为定值,则( )
A.B.
C.D.
变式6.(多选题)(2023·山西大同·高三统考阶段练习)如图,正方体的棱长为2,线段上有两个动点,且,以下结论正确的有( )
A.
B.
C.正方体的体积是三棱锥的体积的12倍
D.异面直线所成的角为定值
变式7.(多选题)(2023·广东深圳·高三红岭中学校考期末)已知正三棱柱ABC﹣A1B1C1的底面边长为1,AA1=1,点P满足,其中λ∈[0,1],μ∈[0,1],下列选项正确的是( )
A.当λ=1时,△AB1P的周长为定值
B.当μ=1时,三棱锥P﹣A1BC的体积为定值
C.当时,有且仅有两个点P,使得A1P⊥BP
D.当时,有且仅有一个点P,使得A1B⊥平面AB1P
变式8.(多选题)(2023·福建厦门·统考模拟预测)如图,在棱长为1的正方体中,点满足,其中,则( )
A.
B.当时,有且仅有一个点,使得平面
C.当时,有且仅有一个点,使得
D.当时,三棱锥的体积为定值
变式9.(多选题)(2023·湖南·校联考模拟预测)如图,为正方体.任作平面与对角线垂直,使得与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l.则( )
A.S为定值B.S不为定值C.l为定值D.l不为定值
变式10.(多选题)(2023·重庆沙坪坝·重庆南开中学校考模拟预测)已知三棱锥,,为棱上一点,且,过点作平行于直线和的平面,分别交棱于.下列说法正确的是( )
A.四边形为矩形
B.四边形的周长为定值
C.四边形的面积为定值
D.当时,平面分三棱锥所得的两部分体积相等
变式11.(多选题)(2023·重庆·统考模拟预测)在正方体中,点P满足,其中,,则下列说法正确的是( )
A.当时,平面
B.当时,三棱锥的体积为定值
C.当时,△PBD的面积为定值
D.当时,直线与所成角的取值范围为
题型三:体积、面积、周长、距离最值与范围问题
例7.(2023·福建福州·福州四中校考模拟预测)在如图所示的试验装置中,两个正方形框架的边长均为2,活动弹子在线段上移动(包含端点),弹子分别固定在线段的中点处,且平面,则当取最大值时,多面体的体积为( )
A.B.C.D.
例8.(2023·山东青岛·高三统考期中)已知正四棱锥的各顶点都在同一个球面上,球的体积为,则该正四棱锥的体积最大值为( )
A.18B.C.D.27
例9.(2023·陕西西安·西安市大明宫中学校考模拟预测)已知正方体的棱长为是正方形(含边界)内的动点,点到平面的距离等于,则两点间距离的最大值为( )
A.B.3C.D.
变式12.(2023·河南·校联考模拟预测)点是圆柱上底面圆周上一动点,是圆柱下底面圆的内接三角形,已知在中,内角、、的对边分别为、、,若,,三棱锥的体积最大值为,则该三棱锥外接球的表面积为( )
A.B.C.D.
变式13.(2023·贵州毕节·校考模拟预测)如图,是半球的直径,为球心,为此半球大圆弧上的任意一点(异于在水平大圆面内的射影为,过作于,连接,若二面角的大小为,则三棱锥的体积的最大值为( )
A.B.C.D.
变式14.(2023·宁夏石嘴山·统考一模)圆锥的底面半径为,母线长为,是圆锥的轴截面,是的中点,为底面圆周上的一个动点(异于、两点),则下列说法正确的是( )
A.存在点,使得B.存在点,使得
C.三棱锥体积最大值为D.三棱锥体积最大值为
变式15.(2023·全国·高三专题练习)已知圆锥SO(O是底面圆的圆心,S是圆锥的顶点)的母线长为,高为1,P、Q为底面圆周上任意两点.有以下三个结论:
①三角形SPQ面积的最大值为2;
②三棱锥体积的最大值为;
③四面体SOPQ外接球表面积的最小值为.
以上所有正确结论的个数为( )
A.0B.1C.2D.3
变式16.(2023·河北·统考模拟预测)在正四面体中,为的中点,点在以为球心的球上运动,,且恒有,已知三棱锥的体积的最大值为,则正四面体外接球的体积为( )
A.B.C.D.
变式17.(2023·湖北恩施·校考模拟预测)如图,矩形ABCD中,E、F分别为BC、AD的中点,且,现将沿AE向上翻折,使点移到P点,则在翻折过程中,下列结论不正确的是( )
A.存在点P,使得
B.存在点P,使得
C.三棱锥的体积最大值为
D.当三棱锥的体积达到最大值时,三棱锥外接球表面积为4π
变式18.(2023·四川成都·四川省成都市玉林中学校考模拟预测)如图,圆台的上、下底面圆半径分别为1、2,高,点S、A分别为其上、下底面圆周上一点,则下列说法中错误的是( )
A.该圆台的体积为
B.直线SA与直线所成角最大值为
C.该圆台有内切球,且半径为
D.直线与平面所成角正切值的最大值为
变式19.(2023·山东·山东省实验中学校考二模)正四棱柱中,,为底面的中心,是棱的中点,正四棱柱的高,点到平面的距离的最大值为( )
A.B.C.D.
变式20.(2023·湖南长沙·长沙一中校考模拟预测)已知A,B,C,D是体积为的球体表面上四点,若,,,且三棱锥A-BCD的体积为,则线段CD长度的最大值为( )
A.B.C.D.
变式21.(2023·全国·高三专题练习)如图,正方形的中心为正方形的中心,,截去如图所示的阴影部分后,翻折得到正四棱锥(,,,四点重合于点),则此四棱锥的体积的最大值为( )
A.B.C.D.
变式22.(2023·安徽黄山·统考二模)如图1,将一块边长为20的正方形纸片剪去四个全等的等腰三角形,,再将剩下的部分沿虚线折成一个正四棱锥,使与重合,与重合,与重合,与重合,点重合于点,如图2.则正四棱锥体积的最大值为( )
A.B.C.D.
变式23.(2023·全国·高三专题练习)如图所示,圆形纸片的圆心为,半径为5,该纸片上的正方形的中心为.,,,为圆上的点,,,,分别是以,,,为底边的等腰三角形.沿虚线剪开后,分别以,,,为折痕折起,使得,,,重合于一点,记为,得到四棱锥.当底面的边长变化时,四棱锥的体积的最大值为( )
A.B.C.D.
题型四:立体几何中的交线问题
例10.(2023·全国·高三校联考阶段练习)已知正方体是半径为的球的内接正方体(八个顶点全部在球面上),则正方体六个面所在的平面与球面的交线总长度是( )
A.B.C.D.
例11.(2023·上海·高三专题练习)直三棱柱中,,,,,设平面与平面的交线为,则与的距离为( ).
A.1B.C.17D.2.6
例12.(2023·浙江·校联考三模)正四面体,为棱的中点,过点作平面的平行平面,该平面与平面、平面的交线分别为,则所成角的正弦值为( )
A.B.C.D.
变式24.(2023·全国·高三专题练习)如图,在棱长为1的正方体中,分别是棱,的中点若经过点的平面与平面的交线为,则与直线所成角的余弦值为( )
A.B.C.D.
变式25.(2023·全国·高三专题练习)在棱长为2的正方体中,,,分别是,,的中点,设过,,的截面与面,以及面的交线分别为,,则,所成的角为( )
A.B.C.D.
变式26.(2023·黑龙江哈尔滨·哈尔滨三中校考模拟预测)在正方体中,为中点,过的截面与平面的交线为,则异面直线与所成角的余弦值为( )
A.B.C.D.
变式27.(2023·全国·高三专题练习)如图,在圆台OO1中,,点C是底面圆周上异于A、B的一点,,点D是BC的中点,l为平面与平面的交线,则交线l与平面所成角的大小为( )
A.B.C.D.
变式28.(2023·河南·高三校联考阶段练习)在正三棱锥P-ABC中,,BC=6,M,N,Q,D分别是AP,BC,AC,PC的中点,平面MQN与平面PBC的交线为l,则直线QD与直线l所成角的正弦值为( )
A.B.C.D.
变式29.(2023·四川成都·高三校联考期末)在正方体中,为线段的中点,设平面与平面的交线为,则直线与所成角的余弦值为( )
A.B.C.D.
变式30.(2023·全国·高三专题练习)如图,在直四棱柱中,,,,,点、分别为棱、的中点,则平面与直四棱柱各侧面矩形的交线所围成的图形的面积为( )
A.B.
C.D.
题型五:空间线段以及线段之和最值问题
例13.(2023·全国·高三专题练习)已知正三棱锥的底面边长为,外接球表面积为,,点M,N分别是线段AB,AC的中点,点P,Q分别是线段SN和平面SCM上的动点,则的最小值为( )
A.B.C.D.
例14.(2023·全国·高三专题练习)已知,如图正三棱锥中,侧棱长为,底面边长为2,D为AC中点,E为AB中点,M是PD上的动点,N是平面PCE上的动点,则最小值是( )
A.B.C.D.
例15.(2023·全国·高三专题练习)如图,在棱长为的正方体中,点是线段上的动点,是上的动点,是上的动点,则长度的最小值为( )
A.B.C.D.
变式31.(2023·辽宁·高一辽宁实验中学校联考期末)如图所示,在直三棱柱中,棱柱的侧面均为矩形,,,,是线段上的一动点,则最小值为( )
A.B.C.D.
变式32.(2023·四川内江·四川省内江市第六中学校考模拟预测)在三棱锥中,,在底面上的投影为的中点,.有下列结论:
①三棱锥的三条侧棱长均相等;
②的取值范围是;
③若三棱锥的四个顶点都在球的表面上,则球的体积为;
④若,是线段上一动点,则的最小值为.
其中所有正确结论的编号是( )
A.①②B.②③C.①②④D.①③④
变式33.(2023·全国·高一专题练习)在四棱锥中,底面,底面为正方形,.点分别为平面,平面和平面内的动点,点为棱上的动点,则的最小值为( )
A.B.C.D.1
变式34.(2023·全国·高三专题练习)在直三棱柱中,,且分别为和的中点,为线段(包括端点)上一动点,为侧面上一动点,则的最小值为( )
A.B.
C.D.
题型六:空间角问题
例16.(2023·全国·高三专题练习)如图,斜三棱柱中,底面是正三角形,分别是侧棱上的点,且,设直线与平面所成的角分别为,平面与底面所成的锐二面角为,则( )
A.
B.
C.
D.
例17.(2023·浙江·高考真题)设三棱锥的底面是正三角形,侧棱长均相等,是棱上的点(不含端点),记直线与直线所成角为,直线与平面所成角为,二面角的平面角为,则
A.B.
C.D.
例18.(2023·浙江·统考高考真题)如图,已知正三棱柱,E,F分别是棱上的点.记与所成的角为,与平面所成的角为,二面角的平面角为,则( )
A.B.C.D.
变式35.(2023·浙江温州·高二温州中学校考期末)斜三棱柱中,底面是正三角形,侧面是矩形,是线段上的动点,记直线与直线所成的角为,直线与平面所成的角为,二面角的平面角为,则( )
A.,B.,
C.,D.,
变式36.(2023·浙江绍兴·高三统考期末)斜三棱柱中,底面是正三角形,侧面是矩形,且,是的中点,记直线与直线所成的角为,直线与平面所成的角为,二面角的平面角为,则( )
A.,B.,
C.,D.,
变式37.(2023·全国·高三专题练习)已知等边,点分别是边上的动点,且满足,将沿着翻折至点处,如图所示,记二面角的平面角为,二面角的平面角为,直线与平面所成角为,则( )
A.B.C.D.
变式38.(2023·江苏·高一专题练习)正四面体中,是侧棱上(端点除外)的一点,若异面直线与直线所成的角为,直线与平面所成的角为,二面角的平面角为,则( )
A.B.
C.D.
变式39.(2023·全国·高三专题练习)在三棱锥中,顶点P在底面的射影为的垂心O(O在内部),且PO中点为M,过AM作平行于BC的截面,过BM作平行于AC的截面,记,与底面ABC所成的锐二面角分别为,,若,则下列说法错误的是( )
A.若,则
B.若,则
C.可能值为
D.当取值最大时,
变式40.(2023·全国·高三专题练习)已知点P是正方体上底面上的一个动点,记面ADP与面BCP所成的锐二面角为,面ABP与面CDP所成的锐二面角为,若,则下列叙述正确的是( )
A.B.
C.D.
变式41.(2023·浙江金华·统考模拟预测)已知四面体中,棱,所在直线所成角为,且,,,面和面所成的锐二面角为,面和面所成的锐二面角为,当四面体的体积取得最大值时( ).
A.B.C.D.不能确定
变式42.(2023·浙江·校联考二模)已知三棱柱的所有棱长均相等,侧棱平面,过作平面与平行,设平面与平面的交线为,记直线与直线所成锐角分别为,则这三个角的大小关系为
A.B.
C.D.
题型七:立体几何装液体问题
例19.(2023·全国·高三专题练习)已知一个放置在水平桌面上的密闭直三棱柱容器,如图1,为正三角形,,,里面装有体积为的液体,现将该棱柱绕旋转至图2.在旋转过程中,以下命题中正确的个数是( )
①液面刚好同时经过,,三点;
②当平面与液面成直二面角时,液面与水平桌面的距离为;
③当液面与水平桌面的距离为时,与液面所成角的正弦值为.
A.0B.1C.2D.3
例20.(2023·全国·高三专题练习)一个密闭且透明的正方体容器中装有部分液体,已知该正方体的棱长为1,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围为( )
A.B.C.D.
例21.(2023·全国·高三专题练习)一个密闭且透明的正方体容器中装有部分液体,已知该正方体的棱长为2,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体的体积的取值范围为( )
A.B.C.D.
变式43.(2023·全国·高三专题练习)已知某圆柱形容器的轴截面是边长为2的正方形,容器中装满液体,现向此容器中放入一个实心小球,使得小球完全被液体淹没,则此时容器中所余液体的最小容量为( )
A.B.C.D.
变式44.(多选题)(2023·辽宁丹东·统考二模)如图,玻璃制成的长方体容器内部灌进一多半水后封闭,仅让底面棱BC位于水平地面上,将容器以BC为轴进行旋转,水面形成四边形EFGH,忽略容器壁厚,则( )
A.始终与水面EFGH平行
B.四边形EFGH面积不变
C.有水部分组成的几何体不可能是三棱柱
D.AE+BF为定值
变式45.(多选题)(2023·全国·高三专题练习)透明塑料制成的正方体密闭容器的体积为64,注入体积为的液体.如图,将容器下底面的顶点置于地面上,再将容器倾斜.随着倾斜度的不同,则下列说法正确的是( )
A.液面始终与地面平行
B.时,液面始终呈平行四边形
C.当时,有液体的部分可呈正三棱锥
D.当液面与正方体的对角线垂直时,液面面积最大值为
变式46.(多选题)(2023·广东广州·高三执信中学校考阶段练习)透明塑料制成的正方体密闭容器的体积为注入体积为的液体.如图,将容器下底面的顶点置于地面上,再将容器倾斜.随着倾斜度的不同,则下列说法正确的是( )
A.液面始终与地面平行
B.时,液面始终是平行四边形
C.当时,有液体的部分可呈正三棱锥
D.当液面与正方体的对角线垂直时,液面面积最大值为
变式47.(多选题)(2023·全国·高三专题练习)向体积为1的正方体密闭容器内注入体积为x()的液体,旋转容器,下列说法正确的是( )
A.当时,容器被液面分割而成的两个几何体完全相同
B.不管注入多少液体,液面都可以成正三角形形状
C.液面可以是正六边形,其面积为
D.当液面恰好经过正方体的某条体对角线时,液面边界周长的最小值为
变式48.(2023·全国·高三专题练习)在一个密闭的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围是 .
变式49.(2023·四川泸州·四川省泸州高级中学校校考一模)一个长、宽、高分别为1、2、3密封且透明的长方体容器中装有部分液体,如果任意转动该长方体,液面的形状都不可能是三角形,那么液体体积的取值范围是 .
【讲通练透】重难点突破05 立体几何中的常考压轴小题(七大题型)-2024年高考数学重难点突破精讲: 这是一份【讲通练透】重难点突破05 立体几何中的常考压轴小题(七大题型)-2024年高考数学重难点突破精讲,文件包含重难点突破05立体几何中的常考压轴小题七大题型原卷版docx、重难点突破05立体几何中的常考压轴小题七大题型解析版docx等2份试卷配套教学资源,其中试卷共100页, 欢迎下载使用。
重难点专题33 立体几何解答题十七大题型汇总-备战2024年高考数学重难点题型突破(新高考新教材通用): 这是一份重难点专题33 立体几何解答题十七大题型汇总-备战2024年高考数学重难点题型突破(新高考新教材通用),文件包含重难点专题33立体几何解答题十七大题型汇总原卷版docx、重难点专题33立体几何解答题十七大题型汇总解析版docx等2份试卷配套教学资源,其中试卷共272页, 欢迎下载使用。
重难点专题32 立体几何压轴小题(体积、角度、外接球等)九大题型汇总-备战2024年高考数学重难点题型突破(新高考新教材通用): 这是一份重难点专题32 立体几何压轴小题(体积、角度、外接球等)九大题型汇总-备战2024年高考数学重难点题型突破(新高考新教材通用),文件包含重难点专题32立体几何压轴小题体积角度外接球等九大题型汇总原卷版docx、重难点专题32立体几何压轴小题体积角度外接球等九大题型汇总解析版docx等2份试卷配套教学资源,其中试卷共120页, 欢迎下载使用。












