2024年湖南省长沙市初中学业水平考试冲刺数学试卷（一）

这是一份2024年湖南省长沙市初中学业水平考试冲刺数学试卷（一），共14页。试卷主要包含了00000011米，数据“0等内容，欢迎下载使用。

温馨提示：
1.答题前，请考生先将自己的姓名、准考证号填写清楚，并认真核对条形码上的姓名、准考证号、考室和座位号；
2.必须在答题卡上答题，在草稿纸、试题卷上答题无效；
3.答题时，请考生注意各大题题号后面的答题提示；
4.请勿折叠答题卡，保持字体工整、笔迹清晰、卡面清洁；
5.答题卡上不得使用涂改液、涂改胶和贴纸；
6.本学科试卷共25个小题，考试时量120分钟，满分120分．
一、选择题（在下列各题的四个选项中，只有一项是符合题意的. 请在答题卡中填涂符合题意的选项. 本大题共10个小题，每小题3分，共30分）
1．某班期末考试数学的平均成绩是83分，小亮得了90分，记作+7分，小英的成绩记作-3分，表示得了（ ）分．
A．86B．83C．87D．80
2．下列计算正确的是（ ）
A．3a+2b=5abB．2a-a=1
C．2a3+3a2=5a5D．-a2b+2a2b=a2b
3．一种纳米材料的直径约为0.00000011米，数据“0.00000011”用科学记数法表示为（ ）
A．1.1×10-6B．1.1×10-7C．1.1×10-8D．11×10-7
4．剪纸艺术是中国民间艺术之一，很多剪纸作品体现了数学中的对称美．如图，蝴蝶剪纸是一幅轴对称图形，将其放在平面直角坐标系中，如果图中点E的坐标为2m,-n，其关于y轴对称的点F的坐标为3-n,-m+1，则m-n的值为（ ）
A．-9B．-1C．0D．1
5．如图，固定木条b，c，使∠1=85°，旋转木条a，要使得a∥b，则∠2应调整为（ ）
A．85°B．90°C．95°D．100°
6．农科院为了解某种小麦的长势，从中随机抽取了部分麦苗，对苗高（单位：cm）进行了测量．根据统计的结果，绘制出如图所示的统计图．这组数据中，众数和中位数分别是（ ）
A．16，15B．16，15.5C．16，16D．17，16
7．劳动课上，八（1）班同学分成两组练习包饺子，女生组包300个饺子与男生组包200个所用的时间相同，已知女生组每分钟比男生组多包30个，若设女生组每分钟包x个，则可列方程为（ ）
A．300x=200x-30B．300x=200x+30
C．300x-30=200xD．300x+30=200x
8．如图，在△ABC中，点D、E、F、G、H分别为AB、BC、AC、DE、EF的中点，则△EGH与△ABC的面积之比为（ ）
A．1:4B．1:8C．1:16D．1:32
9．如图，将半径为6的⊙O沿AB折叠，使得折痕AB垂直半径OC，当AB恰好经过CO的三等分点D（靠近端点O）时，折痕AB长为（ ）
A．82B．415C．8D．45
10．把2，4，7，K四张牌分发给四人，每人按牌面数字分（K记13分）记分，然后收回重洗，再分发和记分，…，若干次后，发现四人累计各得16，17，21和24分．已知得16分者最后一次得2分，则他第一次所得分数是（ ）分．
A．2B．4C．7D．13
二、填空题（本大题共6小题，每小题3分，共18分）
11．分解因式：ax2-a= ．
12．如图为一个五角星图案，将此图案绕中心旋转一定角度后要与原图重合，则旋转的最小角度为 ．
13．从同一副扑克牌中抽出a张红桃，b张黑桃，10张方块，然后洗匀，再从洗匀的这叠扑克牌中抽取一张牌，如果抽出的牌是方块的概率与不是方块的概率相同，那么a、b之间的关系是 ．
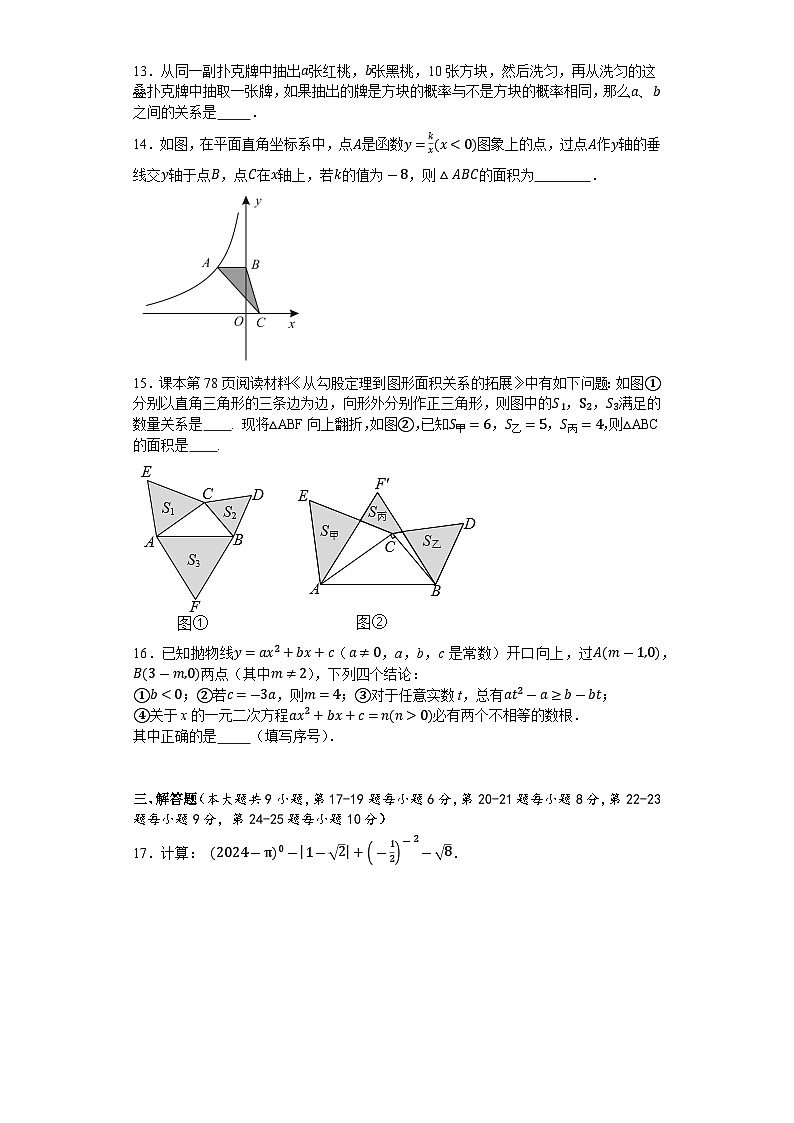
14．如图，在平面直角坐标系中，点A是函数y=kx(x<0)图象上的点，过点A作y轴的垂线交y轴于点B，点C在x轴上，若k的值为-8，则△ABC的面积为 ．
15．课本第78页阅读材料《从勾股定理到图形面积关系的拓展》中有如下问题：如图①分别以直角三角形的三条边为边，向形外分别作正三角形，则图中的S1，S2，S3满足的数量关系是 . 现将△ABF向上翻折，如图②，已知S甲=6，S乙=5，S丙=4，则△ABC的面积是 .
16．已知抛物线y=ax2+bx+c（a≠0，a，b，c是常数）开口向上，过Am-1,0，B3-m,0两点（其中m≠2），下列四个结论：
①b<0；②若c=-3a，则m=4；③对于任意实数t，总有at2-a≥b-bt；
④关于x的一元二次方程ax2+bx+c=nn>0必有两个不相等的数根．
其中正确的是 （填写序号）．
三、解答题（本大题共9小题，第17-19题每小题6分，第20-21题每小题8分，第22-23题每小题9分，第24-25题每小题10分）
17．计算： 2024-π0-1-2+-12-2-8．
18．先化简，再求值．2a2b+3ab-32a2b-ab+1，其中a=-12，b=1．
19．某学校有一栋教学楼AB，小明（身高忽略不计）在教学楼一侧的斜坡底端C处测得教学楼顶端A的仰角为68°，他沿着斜坡向上行走到达斜坡顶端E处，又测得教学楼顶端A的仰角为45°．已知斜坡的坡角（∠ECD）为30°，坡面长度CE＝6m，求楼房AB的高度．（结果精确到0.1m，参考数据：tan68°≈2.48，3≈1.73）
20．为弘扬向善、为善优秀品质，助力爱心公益事业，我校组织“人间自有真情在，爱心助力暖人心”慈善捐款活动，八年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况，统计结果如图①和图②所示.
(1)本次共抽查了________人；并补全上面条形统计图；
(2)本次抽查学生捐款的中位数为________；众数为________；
(3)全校有八年级学生1100人，估计捐款金额超过15元（不含15元）的有多少人？
21．如图，点A,B,C,D在同一条直线上，点E,F分别在直线AB的两侧，且AE=BF,∠A=∠B,∠DCE=∠CDF．
(1)求证：△ACE≌△BDF；
(2)若AB=11,AC=3，求CD的长．
22．学校为了“弘扬传统文化，阅读经典名著”，计划给学校图书馆添置书籍，已知购买3本《论语》和5本《诗经》共需140元，购买8本《论语》和1本《诗经》共需176元．
(1)求每本《论语》和每本《诗经》各多少元？
(2)学校决定购买《论语》和《诗经》共200本，总费用不超过3500元，那么该学校最多可以购买多少本《论语》？
23．在正方形纸片ABCD中，点M、N分别是BC、AD上的点，连接MN．
(1)问题探究：如图1，作DD'⊥MN，交AB于点D'，求证：MN=DD'；
(2)问题解决：如图2，将正方形纸片ABCD沿过点M、N的直线折叠，点D的对应点D'恰好落在AB上，点C的对应点为点C'，若BD'=12，CM=4，求线段MN的长．
24．如图1，△ABC是⊙O的内接三角形，点D在⊙O上，A是弧BD的中点，点E在BC上，连接BD、AE，BD与AE于点F，∠AEB=∠BAC．
(1)求证：AF=BF；
(2)如图2，延长AE交⊙O于点G，连接AO，交BD于点H，求证：AG=2DH；
(3)如图3，在（2）的条件下，作直径BM交AG于点K，连接AM交BD于点N，当AC是⊙O的直径时，MN=25KF，EG=3，求弦BC的长．
25．定义：若一次函数的图象与二次函数的图象有两个交点，并且都在坐标轴上，则称二次函数为一次函数的轴点函数．
【初步理解】
（1）现有以下两个函数：①y=x2-1；②y=x2-x，其中，_________为函数y=x-1的轴点函数．（填序号）
【尝试应用】
（2）函数y=x+c（c为常数，c>0）的图象与x轴交于点A，其轴点函数y=ax2+bx+c与x轴的另一交点为点B.若OB=14OA，求b的值．
【拓展延伸】
（3）如图，函数y=12x+t（t为常数，t>0）的图象与x轴、y轴分别交于M，C两点，在x轴的正半轴上取一点N，使得ON=OC.以线段MN的长度为长、线段MO的长度为宽，在x轴的上方作矩形MNDE.若函数y=12x+t（t为常数，t>0）的轴点函数y=mx2+nx+t的顶点P在矩形MNDE的边上，求n的值．

参考答案与解析
一、选择题
二、填空题
11．ax+1x-1 12．72°/72度 13．a+b=10
14．4 15．S1+S2=S3 7 16．①③④
三、解答题
17．【详解】解：原式=1-2+1+4-22
=6-32 ．
18．【详解】解：2a2b+3ab-32a2b-ab+1
=2a2b+6ab-6a2b+3ab-3
=2a2b-6a2b+6ab+3ab-3
=-4a2b+9ab-3．
当a=-12，b=1时，
原式=-4×14×1+9×-12×1-3
=-1-92-3
=-8.5
19．【详解】过E作EF⊥AB于F，
则四边形BDEF是矩形，
∴EF＝DB，BF＝DE，
在Rt△CDE中，∵∠EDC＝90°CE＝6，∠DCE＝30°，
∴DE＝3，CD＝33，
设BC＝x，
∵∠AEF＝45°，
∴EF＝AF＝BD＝33+x，
∴AB＝AF+BF＝3+33+x，
在Rt△ABC中，tan68°＝ABBC＝3+33+xx＝2.48，
解得：x≈5.5，
经检验x=5.5是所列方程的解，
∴AB＝3+33+x≈13.7米，
答：楼房AB的高度为13.7米．
20．【详解】（1）解： 8÷16%=50（人)，
“捐款为15元”的学生有50-8-14-6-4=18（人)，补全条形统计图如下：
（2）学生捐款金额出现次数最多的是15元，共出现18次，因此捐款金额的众数是15元，
将这50名学生捐款金额从小到大排列处在中间位置的两个数都是15元，因此中位数是15元，
故答案为：15，15；
（3）捐款金额超过15元（不含15元）的人数=1100×6+450=220（人），
所以全校八年级学生为1100名，捐款金额超过15元（不含15元）的人数为220人，
21．【详解】（1）证明：∵∠ACE+∠DCE=180°，∠BDF+∠CDF=180°，且∠DCE=∠CDF，
∴∠ACE=∠BDF，
在△ACE和△BDF中，∠A=∠B∠ACE=∠BDFAE=BF，
∴△ACE≌△BDFAAS．
（2）解：∵△ACE≌△BDF，
∴AC=BD=3，
∵AB=11，
∴CD=AB-AC-BD=11-3-3=5，
∴CD的长为5．
22．【详解】（1）解：设购买每本《论语》需要x元，购买每本《诗经》需要y元，
依题意，得：3x+5y=1408x+y=176，解得：x=20y=16．
答：购买每本《论语》需要20元，购买每本《诗经》需要16元．
（2）设该学校购买m本《论语》，则购买200-m本《诗经》，
依题意，得：20m+16(200-m)≤3500，解得：m≤75．
答：该学校最多可以购买75本《论语》．
23．【详解】（1）解：证明：过点N作NH⊥BC于H，
∵四边形ABCD是正方形，
∴ AD=AB，∠DAB=∠ABM=90°，
∵ ∠NHB=90°，
∴四边形ABHN是矩形，
∴ AB=HN，
∵ DD'⊥MN，
∴ ∠DON=90°，
∴ ∠OND+∠ODN=90°，
∵ ∠OND+∠MNH=90°，
∴ ∠ODN=∠MNH，
∵ ∠DAD'=∠NHM，AD=NH，
∴ △ADD'≌△HNMASA，
∴ MN=DD'；
（2）（2）连接MD'，DD'，
由折叠的性质得到：C'M=CM，CD=C'D'，
设正方形的边长为x，由勾股定理得，BD'2+BM2=D'C'2+C'M2，
∴ 122+x-42=x2+42，
解得：x=18，
∴ AB=AD=18，
∴ AD'=AB-BD'=18-12=6，
由勾股定理得，DD'=AD2+AD'2=182+62=360=610 ，
∵ MN是DD'的垂直平分线，
由（1）知，DD'=MN，
∴ MN=610．
24．【详解】（1）∵∠AEB=∠BAC，
∴∠2+∠C=∠1+∠2，
∴∠C=∠1，
∵A是BD的中点，
∴AB=AD，
∴∠3=∠C，
∴∠3=∠1，
∴AF=BF；
（2）由（1）知，∠1=∠3，
∴BG=AD，∴
∴BG+AB=AD+AB，
即AG=BD，
∴AG=BD，
∵A是BD的中点，
∴AB=AD，
∵AO交BD于点H，
∴BD=2DH，
∴AG=2DH；
（3）如图3，连FO，CG，设∠FOK=α，FK=x，
则MN=25KF=25x，
∵BM为⊙O直径，
∴∠BAM=90°，
∴∠FAN=90°-∠1，∠FNA=90°-∠3，
∵∠1=∠3，
∴∠FAN=∠FNA，
∴FN=FA，
∵FA=FB，
∴FN=FB，
又OB=OM，
∴FO=12MN=5x，
∴KO=FO2-FK2=2x，
∴tanα=FKOK=12，sinα=FKOF=15，
∵AC为⊙O直径，
∴∠ABC=90°，
∴∠BAM+∠ABC=180°，
∴BC∥AM，
∵FO∥AM，
∴OF∥BC，
∴∠4=α，
∵∠BKG=∠G=90°，
∴GC∥BM，
∴∠5=α，
∴在Rt△EGC中，EC=EGsinα=35，GC=EGtanα=3×2=6，
∵AK=GK，AO=CO，
∴OK=12GC=3
设EK=y，则GK=y+3，BK=EKtanα=2y，
∴AK=BKtanα=4y，
∴4y=y+3，
解得，y=1，
即EK=1，
∴BE=EKsinα=5，
∴BC=BE+EC=45．
25．【详解】（1）函数y=x-1交x轴于1,0，交y轴于0,-1，
∵点1,0、0,-1都在y=x2-1函数图象上
∴①y=x2-1为函数y=x-1的轴点函数；
∵点0,-1不在y=x2-x函数图象上
∴②y=x2-x不是函数y=x-1的轴点函数；
故答案为：①；
（2）函数y=x+c交x轴于A-c,0，交y轴于0,c，
∵函数y=x+c的轴点函数y=ax2+bx+c
∴A-c,0和0,c都在y=ax2+bx+c上，
∵c>0
∴OA=c
∵OB=14OA，
∴OB=14c
∴B-14c,0或B14c,0
当B-14c,0时，把A-c,0 B-14c,0代入y=ax2+bx+c得
0=116ac2-14bc+c0=ac2-bc+c，解得b=5，
当B14c,0时，把A-c,0 B14c,0代入y=ax2+bx+c得
0=116ac2+14bc+c0=ac2-bc+c，解得b=-3，
综上，b=5或-3；
（3）函数y=12x+t交x轴于M-2t,0，交y轴于C0,t，
∵ON=OC，以线段MN的长度为长、线段MO的长度为宽，在x轴的上方作矩形MNDE
∴Nt,0，Dt,2t，E-2t,2t,
∵函数y=12x+t（t为常数，t>0）的轴点函数y=mx2+nx+t
∴M-2t,0和C0,t在y=mx2+nx+t上
∴0=m-2t2+n-2t+t，整理得4mt-2n+1=0
∴n=2mt+12
∴y=mx2+nx+t的顶点P坐标为-n2m,4mt-n24m，
∵函数y=mx2+nx+t的顶点P在矩形MNDE的边上
∴可以分三种情况讨论：当P与M重合时；当P在ED上时；当P在DN上时；
当P与M重合时，即-n2m=-2t4mt-n24m=0n=2mt+12，解得n=1；
当P在ED上时，-2t<-n2m此时二次函数开口向下，则m<0
∴-2t<-n2m由n=2mt+12整理得2mt=n-12，
∴2n-12解得n<14，
∴n=-1-2，
当P在DN上时，-n2m=t0≤4mt-n24m≤2tn=2mt+12，整理得2mt=-n=n-12，解得n=14
∴2mt=-14
此时对称轴左边y随x的增大而增大，
∴m<0
∴0≤4mt-n24m≤2t整理得：8mt≤4mt-n2≤0
∴代入2mt=-14、n=14后8mt≤4mt-n2≤0成立
∴n=14，
综上所述，n=1或n=-1-2或n=14
题号
1
2
3
4
5
6
7
8
9
10
选项
D
D
B
D
C
C
A
C
A
C