中考数学一轮复习专题1.1 等腰三角形的性质与判定【十大题型】（举一反三）（北师大版）（原卷版）

这是一份中考数学一轮复习专题1.1 等腰三角形的性质与判定【十大题型】（举一反三）（北师大版）（原卷版），共15页。


TOC \ "1-3" \h \u
\l "_Tc6073" 【题型1 根据等边对等角求角度】 PAGEREF _Tc6073 \h 1
\l "_Tc55" 【题型2 根据等边对等角证明】 PAGEREF _Tc55 \h 3
\l "_Tc12440" 【题型3 根据三线合一求解】 PAGEREF _Tc12440 \h 4
\l "_Tc10903" 【题型4 根据三线合一证明】 PAGEREF _Tc10903 \h 5
\l "_Tc295" 【题型5 根据等腰三角形判定找出图中的等腰三角形】 PAGEREF _Tc295 \h 7
\l "_Tc15870" 【题型6 根据等角对等边证明等腰三角形】 PAGEREF _Tc15870 \h 8
\l "_Tc23381" 【题型7 根据等角对等边证明边相等】 PAGEREF _Tc23381 \h 9
\l "_Tc1900" 【题型8 根据等角对等边求边长】 PAGEREF _Tc1900 \h 11
\l "_Tc14277" 【题型9 求与图形中任意两点构成等腰三角形的个数】 PAGEREF _Tc14277 \h 12
\l "_Tc1551" 【题型10 等腰三角形的判定与性质的综合运用】 PAGEREF _Tc1551 \h 13
【知识点 等腰三角形】
（1）定义：有两边相等的三角形，叫做等腰三角形.
（2）等腰三角形性质
①等腰三角形的两个底角相等，即“等边对等角”；②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合（简称“三线合一”）.特别地，等腰直角三角形的每个底角都等于45°.
（3）等腰三角形的判定
如果一个三角形有两个角相等，那么这两个角所对的边也相等（即“等角对等边”）.
【题型1 根据等边对等角求角度】
【例1】（2023春·江苏无锡·八年级校联考期末）如图，在△ABC中，AC=BC，以点B为旋转中心把△ABC按顺时针方向旋转40°得到△A′BC′，点A′恰好落在AC上，连接CC′，则∠ACC′度数为（ ）

A．110°B．105°C．100°D．95°
【变式1-1】（2023春·广东梅州·八年级校考期末）在△ABC中，AB=AC，BD是AC边上的高，∠ABD=50°，则∠C的度数为 ．
【变式1-2】（2023春·四川达州·八年级校考期中）如图，在第1个△A1BC中，∠B＝30°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E；……按此做法继续下去，则第n个三角形中以An为顶点的内角度数是（ ）

A．12n75°B．12n−165°C．12n−175°D．12n85°
【变式1-3】（2023春·海南海口·八年级校考期中）如图，△ABC中，∠ABC=∠ACB，点D在BC所在的直线上，点E在射线AC上，且∠ADE=∠AED，连接DE．
(1)如图①，∠B=∠C=36°，∠BAD=72°，求∠CDE的度数．
(2)如图②，若∠ABC=∠ACB=65°，∠CDE=20°，求∠BAD的度数．
(3)当点D在直线BC上运动时（不与点B、C重合），试探究∠BAD与∠CDE的数量关系，并说明理由．
【题型2 根据等边对等角证明】
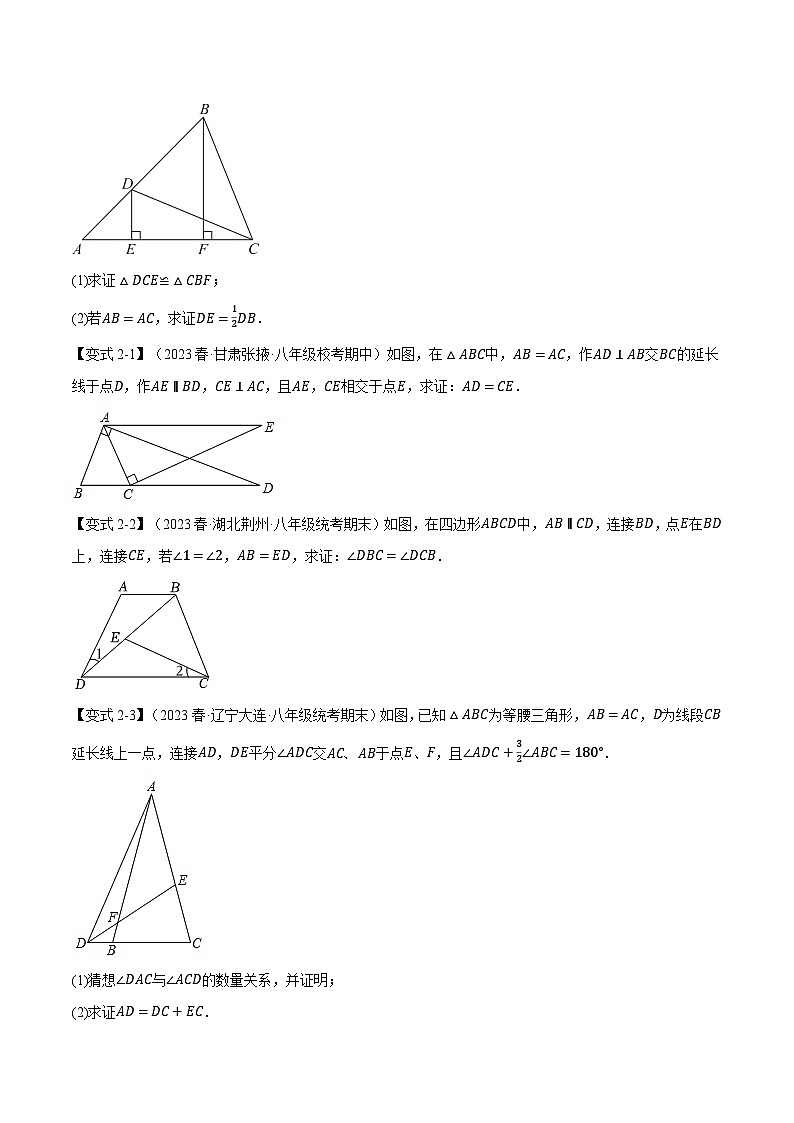
【例2】（2023春·湖南·八年级期末）如图，在△ABC中，∠A=45°，点D在AB边上，BC=CD，DE⊥AC，BF⊥AC，垂足分别为E，F．
(1)求证△DCE≌△CBF；
(2)若AB=AC，求证DE=12DB．
【变式2-1】（2023春·甘肃张掖·八年级校考期中）如图，在△ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作AE∥BD，CE⊥AC，且AE，CE相交于点E，求证：AD=CE．
【变式2-2】（2023春·湖北荆州·八年级统考期末）如图，在四边形ABCD中，AB∥CD，连接BD，点E在BD上，连接CE，若∠1=∠2，AB=ED，求证：∠DBC=∠DCB．
【变式2-3】（2023春·辽宁大连·八年级统考期末）如图，已知△ABC为等腰三角形，AB=AC，D为线段CB延长线上一点，连接AD，DE平分∠ADC交AC、AB于点E、F，且∠ADC+32∠ABC=180°．
(1)猜想∠DAC与∠ACD的数量关系，并证明；
(2)求证AD=DC+EC．
【题型3 根据三线合一求解】
【例3】（2023春·广东深圳·八年级统考期末）如图，△ABC中，AB=AC，点D为CA延长线上一点，DH⊥BC于点H，点F为AB延长线上一点，连接DF交CB的延长线于点E，点E是DF的中点，若BH=2，BE=2BH，则BC= ．

【变式3-1】（2023春·河北邢台·八年级校联考期末）如图，在△ABC中，AB=AC，AD是△ABC的中线，边AB的垂直平分线交AC于点E，连接BE，交AD于点F．若∠C=66°，则∠AFE的度数为（ ）

A．48°B．62°C．72°D．82°
【变式3-2】（2023春·山西临汾·八年级统考期末）如图，在ΔABC中，AB=BC,SΔABC=3cm2，边BC的垂直平分线为l，点D是边AC的中点，点P是l上的动点，当ΔPCD的周长取最小值4时，则AC= ．
【变式3-3】（2023春·辽宁沈阳·八年级统考期末）如图，在△ABC中，∠ACB=90°，AC=BC，点E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G，交AB于点M，点F为边AB上一点，连接CF，∠ACF=∠CBG．
(1)若∠FCM=18°，则∠BGC的度数为______；
(2)若点G是BD的中点，判断CF与DE的数量关系，并说明理由．
【题型4 根据三线合一证明】
【例4】（2023春·福建莆田·八年级校考期中）如图，ΔABC中，AB=AC，AD是BC边上的中线，DE//AC
(1)求证：EB=ED．
(2)求证：AE=DE．
【变式4-1】（2023春·湖南益阳·八年级校考期中）两组邻边分别相等的四边形我们称它为筝形．如图，在筝形ABCD中，AB=AD，BC=DC，AC、BD相交于点O，求证：

(1)△ABC≌△ADC；
(2)AC⊥BD．
【变式4-2】（2023春·山东泰安·八年级统考期中）如图，已知△ABC中，AB=AC，∠BAC=90°，点D为BC的中点，点E、F分别在直线AB、AC上运动，且始终保持AE=CF．
(1)如图①，若点E、F分别在线段AB、AC上，DE与DF相等且DE与DF垂直吗？请说明理由；
(2)如图②，若点E、F分别在线段AB、CA的延长线上，（1）中的结论是否依然成立？说明理由．
【变式4-3】（2023春·河北廊坊·八年级校考期中）如图，在△ABC中，AC=BC,∠A=∠ABC=45°,D为AB中点，点E是AB边上一动点（不含端点A、B），连接CE，点F为CE上一点，BF始终垂直于CE，交直线CD于点G．

(1)点E在线段AD上运动（如图1），当CG=AE时，求证：BG=CE；
(2)若点E运动到线段BD上（如图2），当CG=AE时，试猜想BG、CE的数量关系是否发生变化，请写出你的结论并加以证明；
(3)过点A作AH⊥CE，垂足为点H，并交CD的延长线于点M（如图3），求证：△BCE≌△CAM．
【题型5 根据等腰三角形判定找出图中的等腰三角形】
【例5】（2023春·上海浦东新·八年级校联考期末）已知，如图，在△ABC中，AB＝AC，D，E分别在CA，BA的延长线上，且BE＝CD，连BD，CE．
（1）求证：∠D＝∠E；
（2）若∠BAC＝108°，∠D＝36，则图中共有 个等腰三角形．
【变式5-1】（2023春·广西钦州·八年级校考期中）如图，在Rt△ABC中，∠ACB=90度，BC=4，AC=3，在直线AC上取一点P，使得△PAB为等腰三角形，则符合条件的点P共有（ ）
A．1个B．2个C．3个D．4个
【变式5-2】（2023春·河南南阳·八年级统考期末）如图，△ABC中，∠ABC=72°，∠A=36°，用尺规作图作出射线BD交AC于点D，则图中等腰三角形共有 个．
【变式5-3】（2023春·黑龙江哈尔滨·八年级统考期末）如图1，∠DAB=∠ABC=90°，∠BAC=45°，CE⊥BD．
(1)求证：AD=BE；
(2)如图2，若点E是AB的中点，连接DE、CD，在不添加其他字母的条件下，写出图中四个等腰三角形．
【题型6 根据等角对等边证明等腰三角形】
【例6】（2023春·重庆江北·八年级校考期中）如图，在Rt△ACB中，∠ACB=90°，∠CBA与∠CAB的平分线相交于点E，延长AE交BC于点D，过点E作EF⊥AD交AC于F，作EG∥AB交AC于点G．
(1)求证：△GEF为等腰三角形；
(2)求证：AF+BD=AB．
【变式6-1】（2023春·吉林松原·八年级统考期中）如图，∠1+∠2=180°，GP平分∠BGH．
(1)求证：△PGH是等腰三角形；
(2)若∠1=116°，求∠GPD的度数．
【变式6-2】（2023春·广东广州·八年级校考期末）如图，四边形ABCD中，∠DCB+∠CBA=180°，过点D作∠CDE=∠CAB，DE与C交于点D，与AC交于点H．
(1)求证：△CHD为等腰三角形；
(2)若E为BC中点，猜想AH，HD与EH三者的数量关系．并证明之
【变式6-3】（2023春·新疆乌鲁木齐·八年级统考期末）数学课上，同学们探究下面命题的正确性，顶角为36°的等腰三角形我们称之为黄金三角形，“黄金三角形“具有一种特性，即经过它某一顶点的一条直线可以把它分成两个小等腰三角形，为此，请你，解答问题：
（1）已知如图1：黄金三角形△ABC中，∠A=36°，直线BD平分∠ABC交AC于点D，求证：△ABD和△DBC都是等腰三角形；
（2）如图，在△ABC中，AB=AC，∠A=36°，请你设计三种不同的方法，将△ABC分割成三个等腰三角形，不要求写出画法，不要求证明，但是要标出所分得的每个三角形的各内角的度数．
（3）已知一个三角形可以被分成两个等腰三角形，若原三角形的一个内角为36°，求原三角形的最大内角的所有可能值．
【题型7 根据等角对等边证明边相等】
【例7】（2023春·江苏扬州·八年级统考期末）如图，在△ABC中，∠ABC的平分线BD交AC边于点D，AE⊥BC于点E．已知∠ABC=60°，∠C=45°．

(1)求证：AB=BD；
(2)设BD与AE交于点F，求证：CE=BF+EF．
【变式7-1】（2023春·天津·八年级期中）如图：E在△ABC的AC边的延长线上，AB＝AC，D点在AB边上，DE交BC于点F，DF＝EF，求证：BD＝CE．
【变式7-2】（2023春·湖北孝感·八年级统考期末）如图，△ABC中，CA=CB，点D在BC的延长线上，连接AD，AE平分∠CAD交CD于点E，过点E作EF⊥AB，垂足为点F，与AC相交于点G．
(1)求证：CG=CE；
(2)若∠B=30°，∠CAD=40°，求∠AEF和∠D的度数；
(3)求证：∠D=2∠AEF．
【变式7-3】（2023春·黑龙江哈尔滨·八年级统考期末）已知：在锐角△ABC中，AD为BC边上的高，∠ABD＝2∠CAD．
(1)如图1，求证：AB＝BC；
(2)如图2，点E为AB上一点，且BE＝CD，连接DE，∠AED+∠BDE＝90°，求证∠ABC＝45°；
(3)如图3，在（2）的条件下，过B作BF⊥AC于点F，BF交AD于点G，连接CG，若S△CDG＝2，求△ABG的面积．
【题型8 根据等角对等边求边长】
【例8】（2023春·山东聊城·八年级校考期末）如图，AD为△ABC的角平分线．
(1)如图 1 ，若CE⊥AD于点 F，交AB于点 E ，AB=8 ，AC=5．求 BE的长．
(2)如图 2 ，若∠C=2∠B，点 E 在AB上，且AE=AC，AB=a ，AC=b ，求CD的长；（用含 a 、b 的式子表示）
【变式8-1】（2023春·浙江金华·八年级浙江省义乌市稠江中学校联考期中）如图，上午8时，一艘船从A处出发以15海里/小时的速度向正北航行，10时到达B处，从A,B两点望灯塔C，测得∠NAC=35°,∠NBC=70°，则B处到灯塔C的距离为（ ）
A．45海里B．30海里C．20海里D．15海里
【变式8-2】（2023春·湖北襄阳·八年级校联考期中）如图，将一张长方形纸片ABCD按图中那样折叠，若AE＝5，AB＝12，BE＝13，则重叠部分（阴影）的面积是 ．
【变式8-3】（2023春·辽宁盘锦·八年级校考期中）如图，CE平分∠ACB且CE⊥DB于E，∠DAB=∠DBA，又知AC=14，△CDB的周长为22，则DB的长为( )
A．6B．7C．8D．9
【题型9 求与图形中任意两点构成等腰三角形的个数】
【例9】（2023春·河北邢台·八年级校考期末）题目：“如图，已知∠AOB=30∘，点M，N在边OA上，OM=x，MN=2，P是射线OB上的点，若使点P，M，N构成等腰三角形的点P恰好有3个，求x的取值范围。”对于其答案，甲答：x=0，乙答：0
A．只有甲答的对B．甲、丙答案合在一起才完整
C．甲、乙答案合在一起才完整D．三人答案合在一起才完整
【变式9-1】（2023春·浙江·八年级期中）如图，直线a，b相交于点O，∠1=50°，点A在直线a上，直线b上存在点B，使以点O、A、B为顶点的三角形是等腰三角形，这样的B点有（ ）
A．1个B．2个C．3个D．4个
【变式9-2】（2023春·广东广州·八年级校考期中）如图，△ABC中∠ABC=40°，动点D在直线BC上，当△ABD为等腰三角形，∠ADB= ．

【变式9-3】（2016秋·江苏无锡·八年级统考期中）如图，在△ABC中，AC=BC＞AB，点P为△ABC所在平面内一点，且点P与△ABC的任意两个顶点构成△PAB，△PBC，△PAC均是等腰三角形，则满足上述条件的所有点P的个数为 个．
【题型10 等腰三角形的判定与性质的综合运用】
【例10】（2023春·浙江台州·八年级统考期末）如图，在△ABC中，∠BAC=∠ABC=42°，过点C作CD⊥AB于点D，点E是CD上一点，将△ACE沿着AE翻折得到△AFE，连接CF，若E，F，B三点恰好在同一条直线上，则∠CFA的度数是（ ）
A．75°B．78°C．80°D．84°
【变式10-1】（2023春·黑龙江大庆·八年级校考期中）如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF(E在BC上，F在AC上)折叠，点C与点O恰好重合，则∠OEC为 度．

【变式10-2】（2023春·福建漳州·八年级福建省漳州第一中学校考期末）如图，在△ABC中，D是BC的中点，AD⊥BC，BE⊥AC，延长BE至点M，使得BM=AC，连接AM并延长，交BC的延长线于点N，现给出以下结论：

①AB=BM；
②△ACN≌△BMN；
③AD=DN；
④S△AEM:SBEC=AE:BE.
其中正确的是 .（写出所有正确结论的序号）
【变式10-3】（2023春·四川达州·八年级校考期中）如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．在△ABC外有一点F，使FA⊥AE，FC⊥BC．

(1)求证：BE=CF；
(2)在AB上取一点M，使BM=2DE，连接MC，交AD于点N，连接ME．求证：
①ME⊥BC；
②CM平分∠ACE．
欢迎来到名校课堂【数学学科】
这里是老师交流学习成长的家园，我们一同助力学生成长！