中考数学一轮复习专题1.3 直角三角形【八大题型】（举一反三）（北师大版）（原卷版）

这是一份中考数学一轮复习专题1.3 直角三角形【八大题型】（举一反三）（北师大版）（原卷版），共10页。

TOC \ "1-3" \h \u
\l "_Tc27045" 【题型1 添加条件利用HL使三角形全等】 PAGEREF _Tc27045 \h 1
\l "_Tc9634" 【题型2 判断三角形全等的依据】 PAGEREF _Tc9634 \h 2
\l "_Tc18637" 【题型3 利用HL证明全等】 PAGEREF _Tc18637 \h 4
\l "_Tc15003" 【题型4 利用HL和全等三角形的性质证明线段线段】 PAGEREF _Tc15003 \h 5
\l "_Tc28979" 【题型5 利用HL和全等三角形的性质证明角度相等】 PAGEREF _Tc28979 \h 7
\l "_Tc3985" 【题型6 利用HL解决坐标与图形问题】 PAGEREF _Tc3985 \h 8
\l "_Tc31610" 【题型7 写出某个命题的逆命题】 PAGEREF _Tc31610 \h 9
\l "_Tc31335" 【题型8 判断逆命题的真假】 PAGEREF _Tc31335 \h 10
【知识点1 直角三角形全等的判定】
斜边和一条直角边分别相等的两个直角三角形全等.这一定理简称为“斜边、直角边”或“HL”.
【题型1 添加条件利用HL使三角形全等】
【例1】（2023上·北京海淀·八年级校考期中）阅读下面材料：
已知线段a，b．
求作：Rt△ABC，使得斜边BC=a，一条直角边AC=b．
作法：
（1）作射线AD、AE，且AE⊥AD．
（2）以A为圆心，线段b长为半径作弧，交射线AE于点C．
（3）以C为圆心，线段a长为半径作弧，交射线AD于点B．
（4）连接BC．则△ABC就是所求作的三角形．
上述尺规作图过程中，用到的判定三角形全等的依据是（ ）
A．HLB． SAS C． AAS D． SSA
【变式1-1】（2023下·广东佛山·八年级校考阶段练习）如图，已知AD⊥BC，若用HL判定△ABD≌△ACD，只需添加的一个条件是 ．
【变式1-2】（2023下·山东青岛·八年级统考期中）如图，已知点B，E，F，C在同一条直线上，BE=CF，AB⊥AF，CD⊥DE，若添加一个条件（不再添加新的字母）后，能判定△ABF与△DCE全等，则添加的条件可以是 （写出一个条件即可）．
【变式1-3】（2023下·安徽宿州·八年级统考期末）如图，CD⊥AB于点D，EF⊥AB于点F，CD=EF.要根据“HL”证明Rt△ACD≌Rt△BEF，则还需要添加的条件是（ ）

A．∠A=∠BB．∠C=∠DC．AC=BED．AD=BF
【题型2 判断三角形全等的依据】
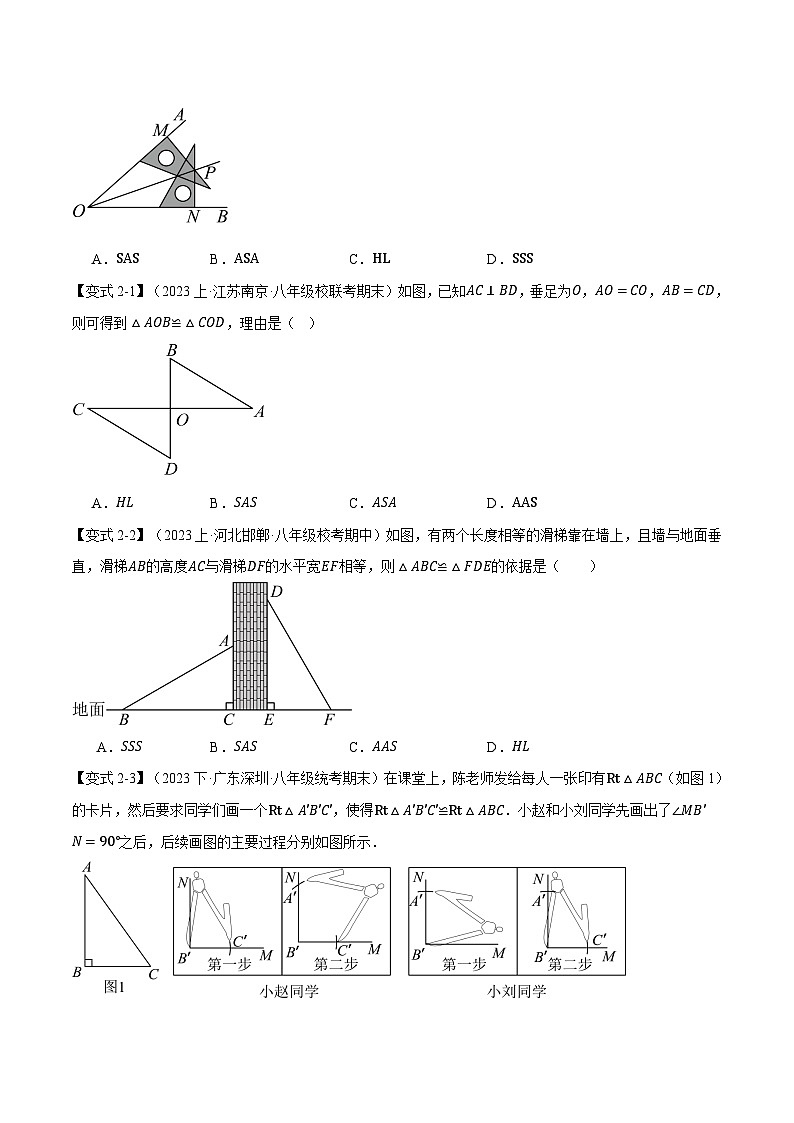
【例2】（2023上·福建泉州·八年级校考期中）如图，用三角尺可以画角平分线：在已知∠AOB的两边上分别取点M，N，使OM=ON，再过点M画OA的垂线，过点N画OB的垂线，两垂线交于点P，画射线OP．可以得到△OMP≌△ONP，所以∠AOP=∠BOP，那么射线OP就是∠AOB的平分线．△OMP≌△ONP的依据是（ ）

A．SASB．ASAC．HLD．SSS
【变式2-1】（2023上·江苏南京·八年级校联考期末）如图，已知AC⊥BD，垂足为O，AO=CO，AB=CD，则可得到△AOB≌△COD，理由是（ ）

A．HLB．SASC．ASAD．AAS
【变式2-2】（2023上·河北邯郸·八年级校考期中）如图，有两个长度相等的滑梯靠在墙上，且墙与地面垂直，滑梯AB的高度AC与滑梯DF的水平宽EF相等，则△ABC≌△FDE的依据是（ ）
A．SSSB．SASC．AASD．HL
【变式2-3】（2023下·广东深圳·八年级统考期末）在课堂上，陈老师发给每人一张印有Rt△ABC（如图1）的卡片，然后要求同学们画一个Rt△A′B′C′，使得Rt△A′B′C′≌Rt△ABC．小赵和小刘同学先画出了∠MB′N=90°之后，后续画图的主要过程分别如图所示．

对这两种画法的描述中正确的是（ ）
A．小赵同学作图判定Rt△A′B′C′≌Rt△ABC的依据是HL
B．小赵同学第二步作图时，用圆规截取的长度是线段BC的长
C．小刘同学作图判定Rt△A′B′C′≌Rt△ABC的依据是ASA
D．小刘同学第一步作图时，用圆规截取的长度是线段AC的长
【题型3 利用HL证明全等】
【例3】（2023·四川泸州·统考模拟预测）如图，AB=CD，DE⊥AC，BF⊥AC，E、是垂足，DE=BF，求证：△ABF≅△CDE．

【变式3-1】（2023上·福建厦门·八年级统考期末）如图是Rt△ABC，根据下列尺规作图痕迹作出的Rt△A1B1C1，能够用于说明“斜边和一条直角边分别相等的两个直角三角形全等”的是（ ）
A． B．
C． D．
【变式3-2】（2023上·河南驻马店·八年级统考期中）学习了全等三角形的判定方法后，我们知道“已知两边和一角分别相等的两个三角形不一定全等”，但下列两种情形还是成立的．

(1)第一种情形（如图a）
在△ABC和△DEF中，∠C=∠F=90°，AC=DF，AB=DE，则根据______，得出△ABC≌△DEF，并写出推理过程；
(2)第二种情形（如图b）
在△ABC和△DEF中，∠C=∠F（∠C和∠F均为钝角），AC=DF，AB=DE，求证：△ABC≌△DEF．（提示：分别过点A、点D添加一条辅助线，构造全等）
【变式3-3】（2023上·山东聊城·八年级校联考阶段练习）如图所示，已知AB=AC,AE=AF,AF⊥BF于F，AE⊥EC于E，则图中全等的三角形共有（ ）

A．4对B．3对C．2对D．1对
【题型4 利用HL和全等三角形的性质证明线段线段】
【例4】（2023上·河北衡水·八年级校考期末）如图，在△ABC中，∠C=90°，∠CAD=∠BAD，DE⊥AB于E，点F在边AC上，连接DF．
(1)求证：AC=AE；
(2)若AC=8，AB=10，求DE的长；
(3)若CF=BE，直接写出线段AB，AF，EB的数量关系．
【变式4-1】（2023下·吉林长春·八年级校考期末）如图，在△ABC中，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为点D、E，CE交AB于点F．

(1)求证：△ACD≌△CBE；
(2)若AC=AF ，AD=12，BE=5，则FE的长______．
【变式4-2】（2023上·山东泰安·八年级统考期中）如图，公路MN和公路PQ在点P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m．假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到噪声影响？请说明理由，如果受影响，已知拖拉机的速度为18km/h，那么学校受影响的时间为多少秒？
【变式4-3】（2023下·湖南张家界·八年级统考期中）如图15，在Rt△ABC中，∠C=90°，AC=10cm，BC=5cm.一条线段PQ=AB，并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等？并说明理由．
【题型5 利用HL和全等三角形的性质证明角度相等】
【例5】湖北武汉·八年级校联考期中如图，有两个长度相等的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠B和∠F的大小有什么关系？
【变式5-1】（2014上·浙江金华·八年级统考期中）已知：在△ABC中，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E、F，且DE=DF．求证：△ABC是等腰三角形．

【变式5-2】（2023上·河北沧州·八年级统考期中）如图，在△ABC中，∠C=90°，AD=AC，DE⊥AB交BC于点E．

（1）△ACE与△ADE是否全等？ ；（填“是”或“否”）
（2）若∠B=28°，则∠AEC的度数为 ．
【变式5-3】（2023下·湖北武汉·八年级校联考期中）如图，在△ABC中，点D是BC的中点，DE⊥AB，DF⊥AC，且DE=DF．
(1)求证：△BDE≌△CDF；
(2)连接AD，求证：AD平分∠BAC．
【题型6 利用HL解决坐标与图形问题】
【例6】（2023上·福建莆田·八年级校考阶段练习）在平面直角坐标系中，A，P分别是x轴、y轴正半轴上的点，B是线段OA上一点，连接PB．
(1)如图1，CA⊥x轴于点A，BC⊥PB，D是OP上一点，且∠BDO=∠PBO；
①求证：∠DBO=∠CBA；
②若OP=OA，求证：BD+BC=BP；
(2)如图2，A5，0，B2，0，G是PB的中点，连接AG，M是x轴负半轴上一点，PM=2AG，当点P在y轴正半轴上运动时，点M的坐标是否会发生变化？若不变，求点M的坐标；若改变，求出其变化的范围．
【变式6-1】（2023上·广东惠州·八年级惠州市第八中学校联考阶段练习）如图，在平面直角坐标系中，AB=CD，OA=OC=1，OB=2，则点D的坐标是 ．

【变式6-2】（2023上·黑龙江哈尔滨·八年级哈尔滨德强学校校考阶段练习）如图，平面直角坐标系中坐标轴上两点A、B，B−23,0，AB=4，∠ABO=30°．
(1)求A点坐标；
(2)点Q为第四象限内一点，点P从点B出发沿x轴正方向运动，速度为2个单位/秒，连接PQ、AQ，AQ交x轴于点D，在运动过程中，∠BPQ始终等于150°，且DA=DQ，请用含t的代数式表示△ABP的面积：
(3)在（2）的条件下，当∠BQA=2∠PBQ，时，求此时P点坐标．
【变式6-3】（2023下·四川成都·八年级校考阶段练习）如图1，在平面直角坐标系中，已知点A，B的坐标分别为（0，3），（3，0）
(1)求直线AB的解析式；
(2)如图2，点C是点B关于y轴的对称点，点D是AB的中点，点P为y轴上自原点向正半轴方向运动的一动点，运动速度为2个单位长度/s，设点P运动的时间为ts，点Q为射线BA上一点，当t=5时，SΔPQOSΔCDB=53，求点Q的坐标；
(3)如图3，在（2）的条件下，当△PDC为等腰直角三角形时，求t的值．
【知识点2 逆命题、逆定理】
两个命题的题设和结论正好相反，我们把这样的两个命题叫做互为逆命题。其中一个叫做原命题，另外一个叫做逆命题。
如果定理的逆命题是正确的，那么它也是一个定理，我们把这个定理叫做原定理的逆定理。
【题型7 写出某个命题的逆命题】
【例7】（2023上·山西吕梁·八年级校考阶段练习）把命题“等腰三角形是轴对称图形”的逆命题改写成“如果…那么……”的形式： ．
【变式7-1】（2023上·八年级课时练习）命题：“等角的余角相等”的条件是 ，结论是： ，逆命题是 ．
【变式7-2】（2023下·江苏盐城·八年级统考期末）命题“如果两个数相等，那么它们的倒数相等”的逆命题是 ．
【变式7-3】（2023·八年级单元测试）将命题“所有直角都相等”的逆命题改写成“如果……那么……”的形式： .
【题型8 判断逆命题的真假】
【例8】（2023上·安徽亳州·八年级统考阶段练习）写出“相等的角是内错角”这个命题的逆命题，并判断原命题和逆命题是不是互逆定理．
【变式8-1】（2023上·浙江衢州·八年级统考期中）下列命题的逆命题是假命题的是（ ）
A．两直线平行，同位角相等；B．对顶角相等；
C．如果a=b，那么a=b；D．线段垂直平分线上的点到线段两端的距离相等
【变式8-2】（2023上·河南周口·八年级统考阶段练习）下列命题的逆命题是假命题的是（ ）
A．两直线平行，内错角相等B．有两个角互余的三角形是直角三角形
C．如果x=y，则x2=y2D．直角都是90°
【变式8-3】（2023下·山东德州·八年级统考期中）已知△ABC，∠A，∠B，∠C的对边分别是a，b，c，下列命题的逆命题成立的是（ ）
A．若∠A=∠C−∠B，则△ABC为直角三角形
B．若a:b:c=3:4:5，则∠C=90°
C．若△ABC为直角三角形，则∠A:∠B:∠C=5:2:3
D．若a2=b+cb−c，则△ABC是直角三角形