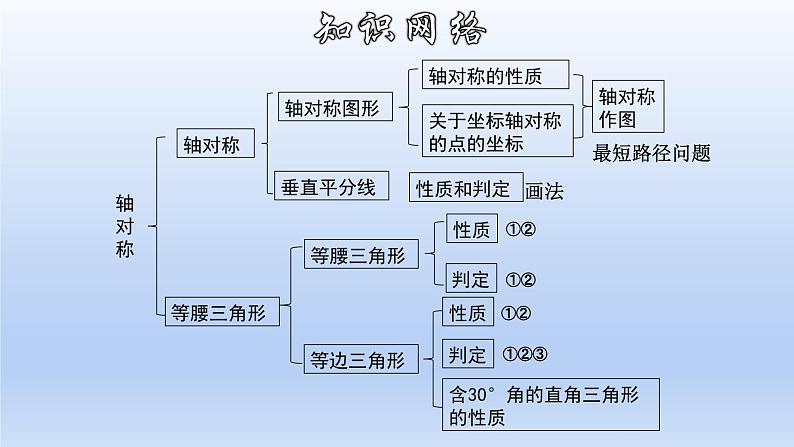
人教版八年级上册13.1.1 轴对称获奖复习ppt课件

这是一份人教版八年级上册13.1.1 轴对称获奖复习ppt课件，共59页。PPT课件主要包含了复习目标，知识网络，轴对称图形，对称轴，知识梳理，垂直平分线，x-y，-xy，-x-y，尺规作图等内容，欢迎下载使用。
1.理解轴对称图形、轴对称的概念、区别及其性质；掌握2个基本的尺规作图；掌握最短路径问题.2.掌握关于坐标轴对称的点的坐标特点，能按要求作出简单平面图形经过一次或两次轴对称后的图形，能指出对称轴.3.掌握线段垂直平分线的性质及判定；掌握等腰(等边)三角形的性质和判定；直角三角形中30°角的性质并解决问题.
一、轴对称相关定义和性质
(1)如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫作____________，这条直线就是它的_________.
(2)如果一个图形沿一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.
(3)轴对称图形的________，是任何一对对应点所连线段的垂直平分线.
(1)关于某直线对称的两个图形是全等图形;
(2)如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的__________；
三、关于坐标轴对称的点的坐标特点
点（x, y）关于x轴对称的点的坐标为 .
点（x, y）关于y轴对称的点的坐标为 .
二、垂直平分线的性质和判定
性质：线段垂直平分线上的点与这条线段两个端点的距离______.
判定：与线段两个______距离相等的点在这条线段的垂直平分线上．
点（x, y）关于原点对称的点的坐标为 .
1.过已知直线外一点作这条直线的垂线(P62)
2.作线段的垂直平分线(P63)
五、等腰三角形的性质及判定
(1)有两边相等的三角形是等腰三角形;
(2)如果一个三角形中有两个角相等,那么这两个角所对的边也相等（简写成“____________”）.
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
等边三角形的性质：1.等边三角形的三边相等.2.等边三角形的三个内角都相等，并每一个角都等于60°.3.等边三角形每条边上的高线、中线、所对角的角平分线都互相重合.4.等边三角形是轴对称图形，有三条对称轴.
六、等边三角形的性质及判定
等边三角形的判定方法：1.三边相等的三角形是等边三角形.2.三个角都相等的三角形是等边三角形.3.有一个角是60°的等腰三角形是等边三角形.
含30°角的直角三角形的性质： 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
七、含30°角的直角三角形的性质
在解决最短路径问题时，我们通常利用轴对称、平移等变化把已知问题转化为容易解决的问题，从而作出最短路径的选择.
【例1】 下列“禁止行人通行、注意危险、禁止非机动车通行、限速60”四个交通标志图中，为轴对称图形的是（　　）
4.将一张正方形纸片按如图①，图②所示的方向对折，然后沿图③中的虚线剪裁得到图④，将图④的纸片展开铺平，再得到的图案是(　　)
【例2】按要求完成作图：(1)作△ABC关于y轴对称的△A1B1C1；(2)在x轴上找出点P，使PA+PC最小，并直接写出P点的坐标；(3)在y轴上找出点Q，使△ABQ周长最小.
解析：(1)△A1B1C1如图所示.(2)P点如图,点P的坐标为(-3,0)（3）如图，点Q即为所求
1.已知点A(m+2，3)和B(-5，n+6)关于x轴对称，则m＝ ， n＝ .2.已知两点A(x1，y1)，B(x2，y2)，如果x1+x2＝0，y1-y2＝0，那么点A和点B关于 对称.
【例3】在△ABC中，AD是高，在线段DC上取一点E，使BD=DE，已知AB+BD=DC.求证：E点在线段AC的垂直平分线上．
解析：要证明点E在线段AC的垂直平分线上，即要证明AE=EC.根据题意及线段垂直平分线的定义，得出AB=AE.而后根据AB+BD=DC，进行等量变换，可到AE=EC.
证明：∵AD是高，∴AD⊥BC，又∵BD=DE，∴AD所在的直线是线段BE的垂直平分线，∴AB=AE，∴AB+BD=AE+DE，又∵AB+BD=DC，∴DC=AE+DE，∴DE+EC=AE+DE∴EC=AE，∴点E在线段AC的垂直平分线上．
【点睛】线段的垂直平分线一般会与中点、90°角、等腰三角形一同出现，在求角度、三角形的周长，或证明线段之间的等量关系时，要注意角或线段之间的转化.
1.如图：△ABC中，MN是AC的垂直平分线，若CM=3cm，△ABC的周长是22cm，则△ABN的周长是 .
2.如图，在△ABC中，DE垂直平分AC交AB于点E，∠A＝30°，∠ACB＝80°，则∠BCE的度数为 .
3.如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F.求证：(1)FC＝AD；(2)AB＝BC＋AD.
证明：(1)∵AD∥BC，∴∠ADC＝∠ECF.∵E是CD的中点，∴DE＝EC.又∵∠AED＝∠CEF，∴△ADE≌△FCE（ASA)，∴FC＝AD.
(2)∵△ADE≌△FCE，∴AE＝EF，AD＝CF.∵BE⊥AE，∴BE是线段AF的垂直平分线，∴AB＝BF＝BC＋CF.∵AD＝CF，∴AB＝BC＋AD.
5.如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．步骤1：以C为圆心，CA为半径画弧①；步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；步骤3：连接AD，交BC延长线于点H．下列叙述正确的是（　　）A．BH垂直平分线段ADB．AC平分∠BADC．S△ABC=BC•AH D．AB=AD
6.如图，已知两条公路AO，BO交于点O，有两个村庄M，N，要修建一座仓库，使仓库到两条公路的距离相等，并且到两个村庄的距离相等，试在图中找到位置并标出.
做线段MN的中垂线与∠AOB的平分线，交点即为所求
如图，AD=BC，AC=BD，求证：△EAB是等腰三角形.
证明：证明：在△ADB和△BCA中，AD=BC，AC=BD，AB=BA，∴△ADB≌△BCA（SSS）．∴∠DBA=∠CAB．∴AE=BE．∴△EAB是等腰三角形．
1.如图，在△ABC中，AB=AC，D为BC的中点，有下列四个结论：①∠B=∠C；②AD⊥BC；③∠BAC=2∠BAD；④
其中正确的有 .（填序号）
2.等腰三角形两边长分别是9 cm和4 cm，则它的周长为________.3.等腰三角形的一个内角等于50°，则它的顶角的度数为__________.4.等腰三角形一腰上的高与另一腰所在的直线的夹角为30°，则它的顶角度数为 .
【点睛】在等腰三角形中，常用到分类讨论思想，一般有如下情况：(1)在求角度时，未指明底角和顶角；(2)在求三角形周长时，未指明底边和腰；(3)未给定图形时，有时需分锐角三角形和钝角三角形两种情况进行讨论.
5.如图，∠A=15°，AB=BC=CD=DE=EF，则∠MEF=　 ．
6.如图，△ABC中，AB=AC，AD⊥BC于D，CE ⊥AB于E，AE=CE. 求证：（1）△AEF≌△CEB； （2）AF=2CD.
证明（1）∵AD⊥BC，CE⊥AB，∴∠BAD+∠B=90°，∠BCE+∠B=90°，∴∠BAD=∠BCE，在△AEF和△CEB中， ∠BAD=∠BCE∵ AE=CE ∠AEF=∠CEB∴△AEF≌△CEB（ASA）；
（2）∵AB=AC，AD⊥BC，∴BD=CD，又知△AEF≌△CEB，∴AF=BC，∴AF=2CD，即AF=6．
7.如图,在△ABC中,AD是角平分线,AC=AB+BD.求证：∠B=2∠C.
证明：在AC上截取AE=AB，连结DE.
∵AD是角平分线，∴∠EAD=∠BAD.
又∵AD=AD，∴△EAD≌△BAD，∴DE=DB，∠AED=∠B.
∵AC=AB+BD=AE+CE=AE+DE，∴CE=DE.
∴∠AED=∠C+∠CDE=2∠C，即∠B=2∠C.
想一想：还有别的证明方法吗？
提示：延长AB至F，使BF=BD，连结DF
8.如图，点A的坐标是(2,2)，若点P在坐标轴上，且△APO是等腰三角形，则点P的个数有____个
1.分情况讨论2.①圆规一转等腰出现 ②线段垂直平分线 (两圆一线）
如图，等边△ABC中，D、E、F分别是各边上的一点，且AD=BE=CF．求证：△DEF是等边三角形．
证明：∵△ABC为等边三角形，且AD=BE=CF∴AF=BD=CE，∠A=∠B=∠C=60°，∴△ADF≌△BED≌△CFE（SAS），∴DF=ED=EF，∴△DEF是等边三角形．
1.等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ，问△APQ是什么形状的三角形？试证明你的结论．
解：△APQ为等边三角形．证明如下：∵△ABC为等边三角形， ∴AB＝AC.∵BP＝CQ，∠ABP＝∠ACQ， ∴△ABP≌△ACQ(SAS)，∴AP＝AQ，∠BAP＝∠CAQ.∵∠BAC＝∠BAP＋∠PAC＝60°∴∠PAQ＝∠CAQ＋∠PAC＝60°∴△APQ是等边三角形．
2.已知如图，点C为线段AB上一点，△ACM、△CBN都是等边三角形，AN交CM于点D，BM交CN于点E，AN交BM于点F.求证：（1）CD=CE;（2）DE∥AB; (3)CF平分∠AFB．
（3）过点C分别作AN,BM的垂线，垂足分别是G,H通过全等或角平分线的判定证明
（1）先证△ACN≌△MCB 再证△ACD≌△MCE(或△CDN≌△CEB) ∴CD=CE
(2)∵CD=CE,∠DCE=60° ∴△DCE是等边三角形 ∴∠EDC=60°=∠ACM ∴DE∥AB
如图在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3cm，则BD的长是( ).A. 3 cm B. 6 cm C. 9 cm D. 12 cm
1.如图,在Rt△ABC中,∠ACB＝90°,∠A=15°,AB边的垂直平分线交AB于点E，交AC于点D，且AD＝18cm，则BC的长是 .
2.如图所示，点P是∠AOB平分线上的一点，过点P作PC∥OA交OB于点C，若∠AOB＝30°，OC＝4,点P到OA的距离PD= .
3.某校在一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a元，则购买这种草皮至少要______元．
4.如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
证明：连接AF，∵AB=AC，∠BAC=120°，∴∠B=∠C=30°，∵AC的垂直平分线EF交AC于点E，交BC于点F，∴CF=AF，∴∠FAC=∠C=30°，∴∠BAF=∠BAC-∠FAC=120°-30°=90°，在Rt△ABF中，∠B=30°，∴BF=2AF，∴BF=2CF．
如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD=5,点F是AD边上的动点，则BF+EF的最小值为（　　）A．7.5 B．5 C．4 D．不能确定
解析：△ABC为等边三角形，点D是BC边的中点，即点B与点C关于直线AD对称.∵点F在AD上，故BF=CF.即BF+EF的最小值可转化为求CF+EF的最小值，故连接CE即可，线段CE的长即为BF+EF的最小值.
1.如图，直线l是一条河，P、Q是两个村庄．欲在l上的某处修建一个水泵站,向P、Q两地供水，现有如下四种铺设方案,图中实线表示铺设的管道，则所需管道最短的是( )
2.已知：如图，∠AOB内一点P，P1，P2分别P是关于OA、OB的对称点，P1P2交OA于M，交OB于N，若P1P2=5cm，则△PMN的周长是（　　）
A. 3cm B. 4cm C. 5cm D. 6cm
利用轴对称解决最小值问题
3.如图，四边形ABCD中,∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，∠AMN＋∠ANM的度数是（ ）.
轴对称解决最短路径问题
A．130° B．120° C．110° D．100°
1.已知点P (3, -1)关于y轴的对称点Q的坐标是(a+b, 1-b)，则ab的值为_____.2.将一副三角尺按如图所示方式叠放在一起,若AB=16cm，则阴影部分的面积是_____cm2.
3.如图，∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4…均为等边三角形．若OA1＝1，则△AnBnAn＋1的边长为______.
4.如图，在直角坐标系中，点A，B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A，B，C三点不在同一条直线上，当△ABC的周长最小时点C的坐标是（　　）A．（0，3） B．（0，2） C．（0，1） D．（0，0）
5.如图，已知∠MON=40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，∠APB的度数是 .
6..如图，P,Q是△ABC的边BC上的两点，并且BP=PQ=QC=AP=AQ,求∠BAC的度数..
解：∵PA=PQ=AQ，∴∠APQ=∠PQA=∠QAP=60°∵PA=PB，∴∠B=∠PAB又∠B+∠PAB=60°∴∠PBA=∠PAB=30°，同理∠QAC=30°。∴∠BAC=∠BAP+∠PAQ+∠QAC=30°+60°+30°=120°
7.已知，如图，△ABC为等边三角形，点E在AC边上，点D在BC边上，并且AE＝CD，AD和BE相交于点M，BN⊥AD于N．(1)求证：BE＝AD；(2)求∠BMN的度数；(3)若MN＝3cm，ME＝1cm，则AD＝　 　cm．
8.如图，点D在线段BC上，连接AD，BD=CD，CA⊥AD，∠1=30°，AB=4，求AC的长．
9.如图，等边△ABC的边长为8，D为AB边上一动点，过点D作DE⊥BC于点E，过点E作EF⊥AC于点F.(1)若AD=2，求AF的长; (2)当AD取何值时，DE=EF?
解：（1）∵AB=8，AD=2∴BD=AB-AD=6在Rt△BDE中∠BDE=90°-∠B=30°∴BE= BD=3∴CE=BC-BE=5在Rt△CFE中∠CEF=90°-∠C=30°∴CF= CE=∴AF=AC-FC= ；
1.已知：如图，△ABC是边长为3 cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1 cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t(s)．(1)当动点P、Q同时运动2 s时，则BP＝__cm，BQ＝__cm.(2)当动点P、Q同时运动t(s)时，分别用含有t的式子表示：BP＝________cm，BQ＝__cm.(3)当t为何值时，△PBQ是直角三角形？