人教版八年级上册13.3.1 等腰三角形完美版ppt课件

这是一份人教版八年级上册13.3.1 等腰三角形完美版ppt课件，共22页。PPT课件主要包含了复习提问，学习目标，自学指导，自主学习3分钟，探究新知，等腰三角形的判定，∵AD∥BC，检测一，探索新知，+5分钟等内容，欢迎下载使用。

如图,位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
本题的本质是证明____＝____.
你能把本题改编成一道证明题吗？
1 .掌握等腰三角形的判定方法.（重点）2.掌握等腰三角形的判定定理，并运用其进行证明和计 算.（难点）
自主学习课本77页思考以下，完成自主学习部分
独立完成学案上自主学习一，同桌讨论交流
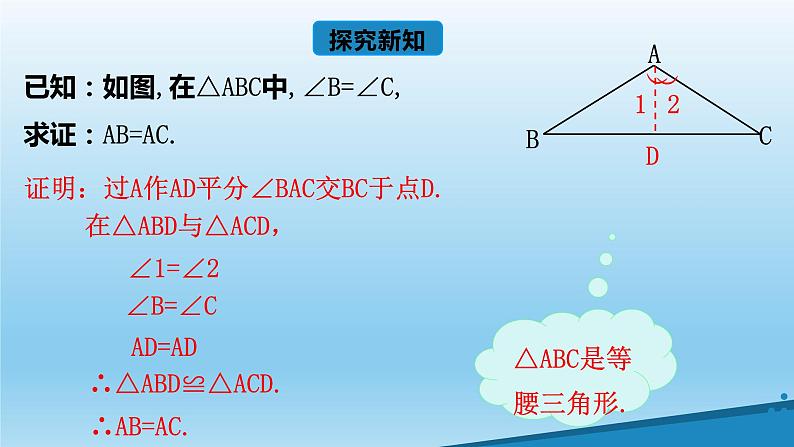
已知：如图,在△ABC中,∠B=∠C,求证：AB=AC.
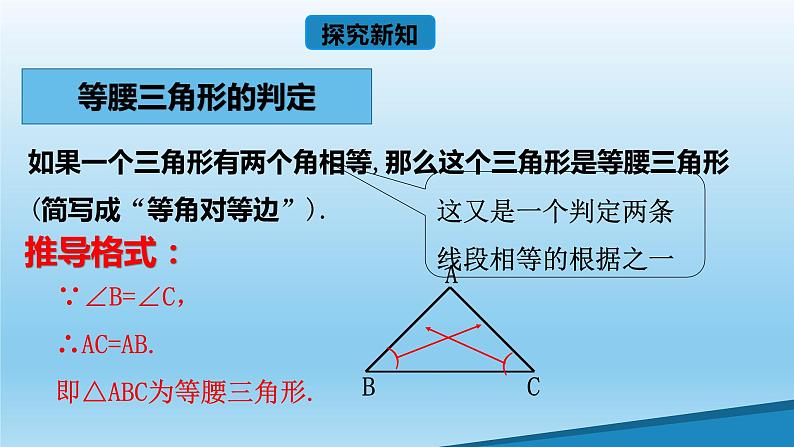
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
这又是一个判定两条线段相等的根据之一
∴AC=AB.即△ABC为等腰三角形.
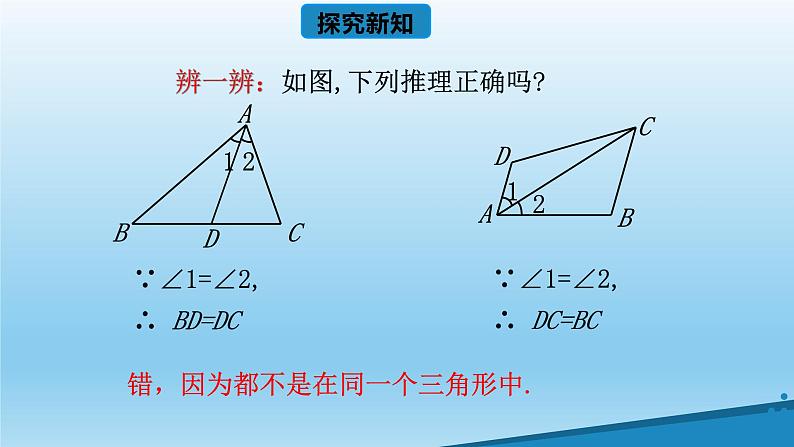
错，因为都不是在同一个三角形中.
【例2】已知：如图,AB=DC,BD=CA,BD与CA相交于点E. 求证：△AED是等腰三角形.
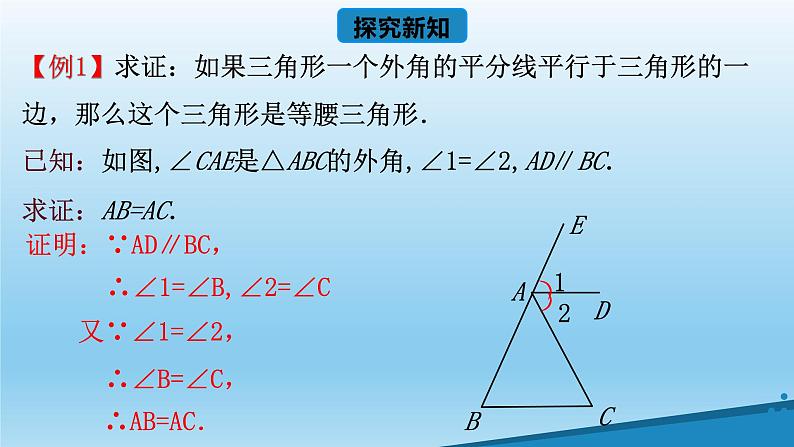
【例3】已知：如图，AD∥BC，BD平分∠ABC. 求证：AB=AD
证明：∵AD∥BC， ∴∠ADB=∠DBC. ∵BD平分∠ABC， ∴∠ABD=∠DBC， ∴∠ABD=∠ADB， ∴AB=AD.
总结：平分角+平行=等腰三角形
如图，已知OC平分∠AOB，CD∥OB，若OD＝3cm，则CD等于_______.
如图，把一张长方形的纸沿着对角线折叠，重合部分是一个等腰三角形吗？为什么？
由折叠可知，∠EBD=∠CBD.
∴∠EDB=∠EBD，∴BE=DE，△EBD是等腰三角形.
∴∠EDB=∠CBD，
例4 如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，AE是∠BAC的平分线，AE与CD交于点F，求证：△CEF是等腰三角形．
证明：∵在△ABC中，∠ACB＝90°，∴∠B＋∠BAC＝90°.∵CD是AB边上的高，∴∠ACD＋∠BAC＝90°，∴∠B＝∠ACD.∵AE是∠BAC的平分线，∴∠BAE＝∠EAC，∴∠B＋∠BAE＝∠ACD＋∠EAC，即∠CEF＝∠CFE，∴CE＝CF，∴△CEF是等腰三角形．
通过计算角相等来证明等腰三角形
“等角对等边”是判定等腰三角形的重要依据，它的前提条件是“在同一个三角形中”．
自主学习（3分钟）5分钟合作交流
自主学习课本78页例3
例4 已知等腰三角形底边长为a,底边上的高的长为h，求作等腰△ABC.使底边BC=a，底边上的高为h.
作法：1.作线段AB=a.2.作线段AB的垂直平分线MN，交AB 于点D.3.在MN上取一点C，使DC=h.4.连接AC，BC，则△ABC即为所求.
利用尺规作图作等腰三角形
例5 如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E，交AC于F.探究EF，BE，FC之间的关系.
解：EF=BE+CF.理由如下：∵ EF∥BC,∴∠EOB=∠CBO，∠FOC=∠BCO. ∵ BO，CO分别平分∠ABC，∠ACB，∴∠CBO＝∠ABO，∠BCO＝∠ACO，∴∠EOB＝∠ABO ，∠FOC＝∠ACO，∴BE＝OE，CF=OF，∴ EF=EO+FO＝BE+CF.
利用等腰三角形的判定证明线段之间的关系
判定线段之间的数量关系，一般做法是通过证明线段所在的两个三角形全等或利用同一个三角形中“等角对等边”，运用转化思想，解决问题.
在ΔABC中,OB平分∠ABC， OC平分∠ACB，过O点作MN ∥BC.
ΔAMN的周长=AB+AC吗？为什么？
解：∵ OB平分∠ABC，∴∠1=∠2，又 ∵MN∥BC，∴∠2=∠3，∴∠1=∠3.∴OM=BM.同理得：ON=CN.
趣味拓展：如图,在△ABC中,AB=AC, ∠A=36°,你能在△ABC内部添加两条线段，将其分成若干个等腰三角形吗?(提供两中以上不同的作图方案)
1．(2023.宿迁)若等腰三角形有一个内角为110°，则这个等腰三角形的底角是（　C　）A．70°B．45° C．35° D．50°
2.（2023.锦州）如图，在△ABC中，BC的垂直平分线交BC于点D，交AB于点E，连接CE．若CE＝CA，∠ACE＝40°，则∠B的度数为 　 35°　 　．
3．(2023.廊坊)如图，在△ABC中，CD平分∠ACB，AE⊥CD，垂足为点E，过点E 作EF∥BC，交AC于点F，G为BC的中点，连接FG．求证：FG＝